|
Small Retrosnub Icosicosidodecahedron
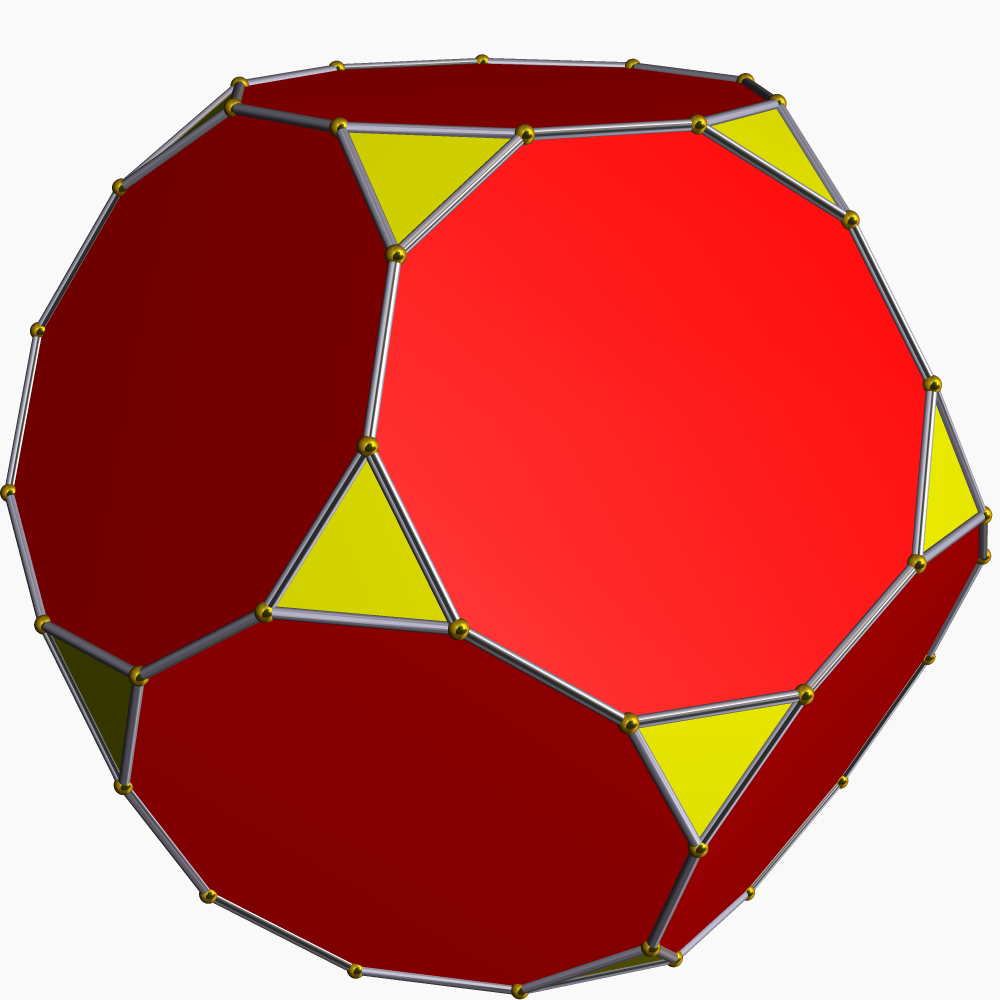
In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as . It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. It is given a Schläfli symbol sr The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries. George Olshevsky nicknamed it the yog-sothoth (after the Cthulhu Mythos deity). Convex hull Its convex hull is a nonuniform truncated dodecahedron. Cartesian coordinates Cartesian coordinates for the vertices of a small retrosnub icosicosidodecahedron are all the even permutations of : (±(1-ϕ−α), 0, ±(3−ϕα)) : (±(ϕ-1−α), ±2, ±(2ϕ-1−ϕα)) : (±(ϕ+1−α), ±2(ϕ-1), ±(1−ϕα)) where ϕ = (1+)/2 is the golden ratio and α = . See also * Lis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Retrosnub Icosicosidodecahedron
In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as . It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. It is given a Schläfli symbol sr The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries. George Olshevsky nicknamed it the yog-sothoth (after the Cthulhu Mythos deity). Convex hull Its convex hull is a nonuniform truncated dodecahedron. Cartesian coordinates Cartesian coordinates for the vertices of a small retrosnub icosicosidodecahedron are all the even permutations of : (±(1-ϕ−α), 0, ±(3−ϕα)) : (±(ϕ-1−α), ±2, ±(2ϕ-1−ϕα)) : (±(ϕ+1−α), ±2(ϕ-1), ±(1−ϕα)) where ϕ = (1+)/2 is the golden ratio and α = . See also * Lis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Dodecahedron
In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges. Geometric relations This polyhedron can be formed from a regular dodecahedron by truncating (cutting off) the corners so the pentagon faces become decagons and the corners become triangles. It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated icosahedral honeycomb. Area and volume The area ''A'' and the volume ''V'' of a truncated dodecahedron of edge length ''a'' are: :\begin A &= 5 \left(\sqrt+6\sqrt\right) a^2 &&\approx 100.990\,76a^2 \\ V &= \tfrac \left(99+47\sqrt\right) a^3 &&\approx 85.039\,6646a^3 \end Cartesian coordinates Cartesian coordinates for the vertices of a truncated dodecahedron with edge length 2''φ'' − 2, centered at the origin, are all even permutations of: :(0, ±, ±(2 + ''φ'')) :(±, ±''φ'', ±2''φ'') :(±''φ'', ±2, ±(''φ'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Uniform Polyhedra
In geometry, a uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive ( transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent, and the polyhedron has a high degree of reflectional and rotational symmetry. Uniform polyhedra can be divided between convex forms with convex regular polygon faces and star forms. Star forms have either regular star polygon faces or vertex figures or both. This list includes these: * all 75 nonprismatic uniform polyhedra; * a few representatives of the infinite sets of prisms and antiprisms; * one degenerate polyhedron, Skilling's figure with overlapping edges. It was proven in that there are only 75 uniform polyhedra other than the infinite families of prisms and antiprisms. John Skilling discovered an overlooked degenerate example, by relaxing the condition that only two faces may meet at an edge. This is a degenerate u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
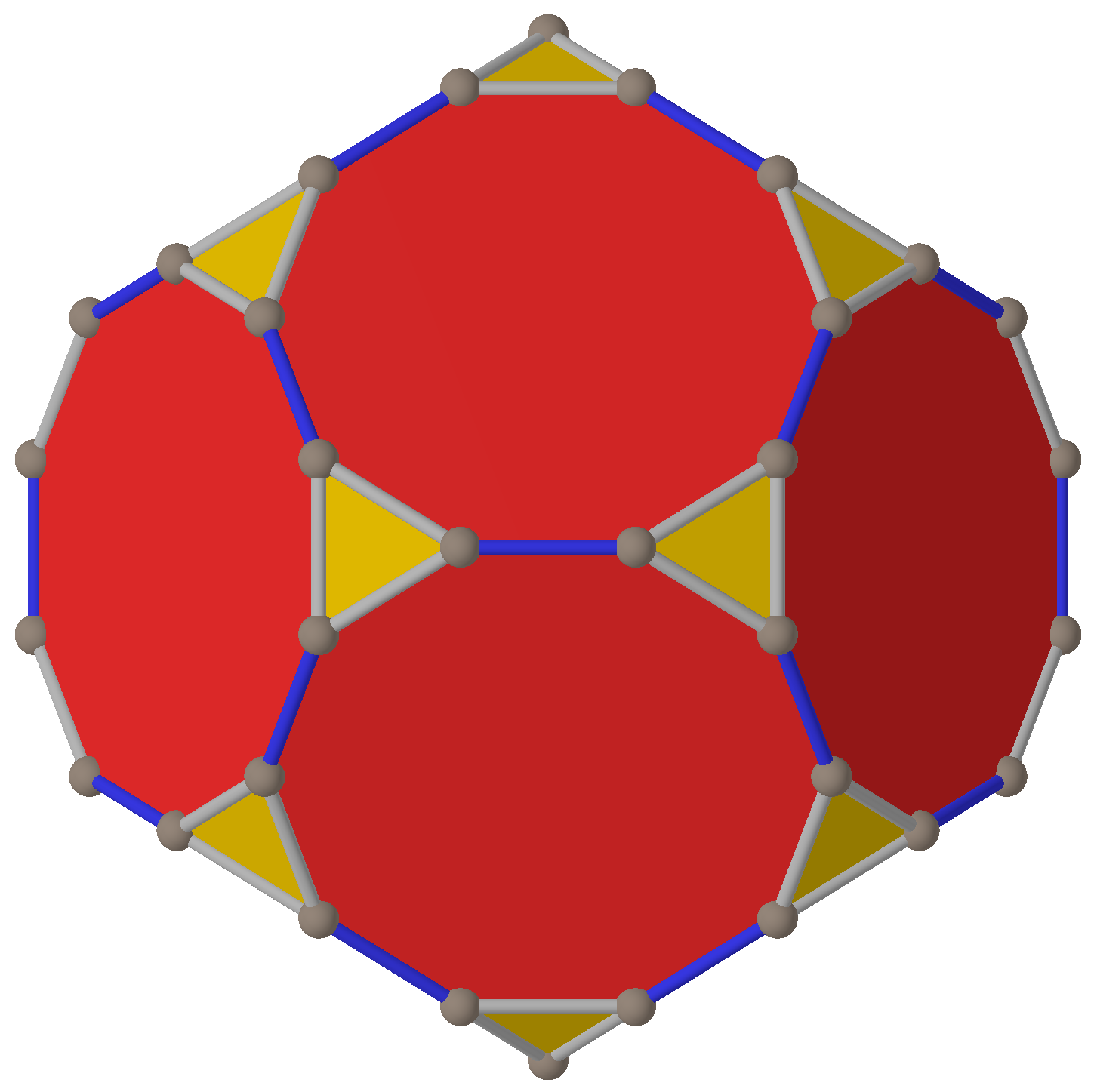
Small Retrosnub Icosicosidodecahedron Convex Hull
{{disambiguation ...
Small may refer to: Science and technology * SMALL, an ALGOL-like programming language * Small (anatomy), the lumbar region of the back * ''Small'' (journal), a nano-science publication * <small>, an HTML element that defines smaller text Arts and entertainment Fictional characters * Small, in the British children's show Big & Small Other uses * Small, of little size * Small (surname) * "Small", a song from the album ''The Cosmos Rocks'' by Queen + Paul Rodgers See also * Smal (other) * List of people known as the Small * Smalls (other) Smalls may refer to: * Smalls (surname) * Camp Robert Smalls, a United States Naval training facility * Fort Robert Smalls, a Civil War redoubt * Smalls Creek, a northern tributary of the Parramatta River * Smalls Falls, a waterfall in Maine, USA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Dodecahedron
In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges. Geometric relations This polyhedron can be formed from a regular dodecahedron by truncating (cutting off) the corners so the pentagon faces become decagons and the corners become triangles. It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated icosahedral honeycomb. Area and volume The area ''A'' and the volume ''V'' of a truncated dodecahedron of edge length ''a'' are: :\begin A &= 5 \left(\sqrt+6\sqrt\right) a^2 &&\approx 100.990\,76a^2 \\ V &= \tfrac \left(99+47\sqrt\right) a^3 &&\approx 85.039\,6646a^3 \end Cartesian coordinates Cartesian coordinates for the vertices of a truncated dodecahedron with edge length 2''φ'' − 2, centered at the origin, are all even permutations of: :(0, ±, ±(2 + ''φ'')) :(±, ±''φ'', ±2''φ'') :(±''φ'', ±2, ±(''φ'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yog-Sothoth
American author H. P. Lovecraft (1890–1937) created a number of fictional deities throughout the course of his literary career. These entities are usually depicted as immensely powerful and utterly indifferent to humans who can barely begin to comprehend them, though some entities are worshipped by humans. These deities include the "Great Old Ones" and extraterrestrials, such as the "Elder Things", with sporadic references to other miscellaneous deities (e.g. Nodens). The "Elder Gods" are a later creation of other prolific writers who expanded on Lovecraft's concepts, such as August Derleth, who was credited with formalizing the Cthulhu Mythos. Most of these deities were Lovecraft's original creations, but he also adapted words or concepts from earlier writers such as Ambrose Bierce, and later writers in turn used Lovecraft's concepts and expanded his fictional universe. Great Old Ones An ongoing theme in Lovecraft's work is the complete irrelevance of humanity in the face of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°. Regular hexagon A ''regular polygon, regular hexagon'' has Schläfli symbol and can also be constructed as a Truncation (geometry), truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral polygon, equilateral and equiangular polygon, equiangular. It is bicentric polygon, bicentric, meaning that it is both cyclic polygon, cyclic (has a circumscribed circle) and tangential polygon, tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed figure, inscribed circle). All internal angles are 120 degree (angle), degrees. A regular hexago ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |