|
Small Object Argument
In mathematics, especially in category theory, Quillen’s small object argument, when applicable, constructs a factorization of a morphism in a functorial way. In practice, it can be used to show some class of morphisms constitutes a weak factorization system in the theory of model categories. The argument was introduced by Quillen to construct a model structure on the category of (reasonable) topological spaces. The original argument was later refined by Garner. Statement Let C be a category that has all small colimits. We say an object x in it is compact with respect to an ordinal \omega if \operatorname(x, -) commutes with an \omega-filterted colimit. In practice, we fix \omega and simply say an object is compact if it is so with respect to that fixed \omega. If F is a class of morphismms, we write l(F) for the class of morphisms that satisfy the left lifting property with respect to F. Similarly, we write r(F) for the right lifting property. Then Example: presheaf Her ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
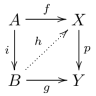
Weak Factorization System
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory. Definition A factorization system (''E'', ''M'') for a category C consists of two classes of morphisms ''E'' and ''M'' of C such that: #''E'' and ''M'' both contain all isomorphisms of C and are closed under composition. #Every morphism ''f'' of C can be factored as f=m\circ e for some morphisms e\in E and m\in M. #The factorization is ''functorial'': if u and v are two morphisms such that vme=m'e'u for some morphisms e, e'\in E and m, m'\in M, then there exists a unique morphism w making the following diagram commute: ''Remark:'' (u,v) is a morphism from me to m'e' in the arrow category In mathematics, a comma category (a special case being a slice category) is a construction in category theory. It provides another way of looking at morphisms: instead o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Object (mathematics)
In mathematics, compact objects, also referred to as finitely presented objects, or objects of finite presentation, are objects in a category satisfying a certain finiteness condition. Definition An object ''X'' in a category ''C'' which admits all filtered colimits (also known as direct limits) is called ''compact'' if the functor :\operatorname_C(X, \cdot) : C \to \mathrm, Y \mapsto \operatorname_C(X, Y) commutes with filtered colimits, i.e., if the natural map :\operatorname \operatorname_C(X, Y_i) \to \operatorname_C(X, \operatorname_i Y_i) is a bijection for any filtered system of objects Y_i in ''C''. Since elements in the filtered colimit at the left are represented by maps X \to Y_i, for some ''i'', the surjectivity of the above map amounts to requiring that a map X \to \operatorname_i Y_i factors over some Y_i. The terminology is motivated by an example arising from topology mentioned below. Several authors also use a terminology which is more closely related to algebr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Left Lifting Property
In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples. Formal definition A morphism i in a category has the ''left lifting property'' with respect to a morphism p, and p also has the ''right lifting property'' with respect to i, sometimes denoted i\perp p or i\downarrow p, iff the following implication holds for each morphism f and g in the category: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anodyne Extension
In mathematics, especially in homotopy theory, a left fibration of simplicial sets is a map that has the right lifting property with respect to the horn inclusions \Lambda^n_i \subset \Delta^n, 0 \le i < n. A right fibration is defined similarly with the condition . A is one with the right lifting property with respect to every horn inclusion; hence, a Kan fibration is exactly a map that is both a left and right fibration. Examples A right fibration is a cartesian fibration such that each fiber is a . In particular, a[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |