|
Slopes Of Purdown, Bristol, England Arp
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is used for slope, but its earliest use in English appears in O'Brien (1844) who wrote the equation of a straight line as and it can also be found in Todhunter (1888) who wrote it as "''y'' = ''mx'' + ''c''". Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line. Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line. A line that is decreasing has a negative "rise". The line may be practical – as set by a road surveyor, or in a diagram that models a road or a roof either as a description or as a plan. The ''steepness'', incline, or grade of a line is measured by the absolute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiki Slope In 2d
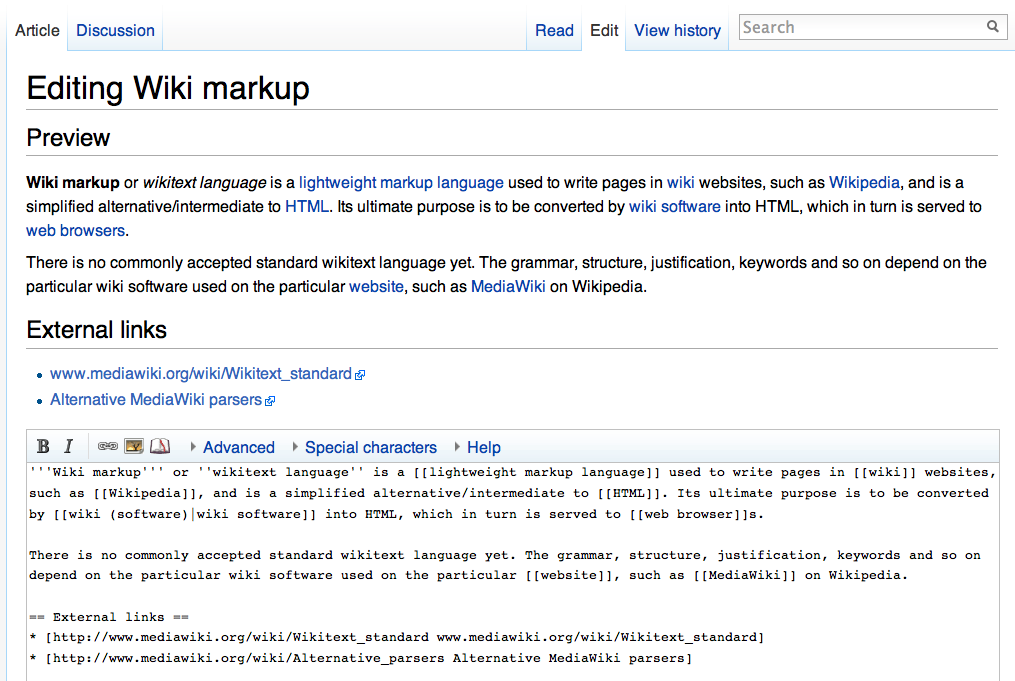
A wiki ( ) is an online hypertext publication collaboratively edited and managed by its own audience, using a web browser. A typical wiki contains multiple pages for the subjects or scope of the project, and could be either open to the public or limited to use within an organization for maintaining its internal knowledge base. Wikis are enabled by wiki software, otherwise known as wiki engines. A wiki engine, being a form of a content management system, differs from other web-based systems such as blog software, in that the content is created without any defined owner or leader, and wikis have little inherent structure, allowing structure to emerge according to the needs of the users. Wiki engines usually allow content to be written using a simplified markup language and sometimes edited with the help of a rich-text editor. There are dozens of different wiki engines in use, both standalone and part of other software, such as bug tracking systems. Some wiki engines are ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |