|
Sliding DFT
In applied mathematics, the sliding discrete Fourier transform is a recursive algorithm to compute successive STFTs of input data frames that are a single sample apart (hopsize − 1). The calculation for the sliding DFT is closely related to Goertzel algorithm. Definition Assuming that the hopsize between two consecutive DFTs is 1 sample, then \begin F_(n) &= \sum_^ f_e^\\ &= \sum_^N f_e^ \\ &= e^ \left \sum_^ f_e^ - f_t + f_ \right\\ &= e^ \left _t(n) - f_t + f_ \right \end From this definition above, the DFT can be computed recursively thereafter. However, implementing the window function In signal processing and statistics, a window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around ... on a sliding DFT is difficult due to its recursive nature, therefore it is done exclusively in a frequency domain. Sliding wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur. A process that exhibits recursion is ''recursive''. Video feedback displays recursive images, as does an infinity mirror. Formal definitions In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties: * A simple ''base case'' (or cases) — a terminating scenario that does not use recursion to produce an answer * A ''recursive step'' — a set of rules that reduces all successive cases ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goertzel Algorithm
The Goertzel algorithm is a technique in digital signal processing (DSP) for efficient evaluation of the individual terms of the discrete Fourier transform (DFT). It is useful in certain practical applications, such as recognition of dual-tone multi-frequency signaling (DTMF) tones produced by the push buttons of the keypad of a traditional analog telephone. The algorithm was first described by Gerald Goertzel in 1958. Like the DFT, the Goertzel algorithm analyses one selectable frequency component from a discrete signal. Unlike direct DFT calculations, the Goertzel algorithm applies a single Real number, real-valued coefficient at each iteration, using real-valued arithmetic for real-valued input sequences. For covering a full spectrum (except when using for continuous stream of data where coefficients are reused for subsequent calculations, which has computational complexity equivalent of sliding DFT), the Goertzel algorithm has a Computational complexity theory, higher order of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Window Function
In signal processing and statistics, a window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions. The reasons for examining segments of a longer function include detection of transient events and time-averaging of frequency spectra. The duration of the segments is determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
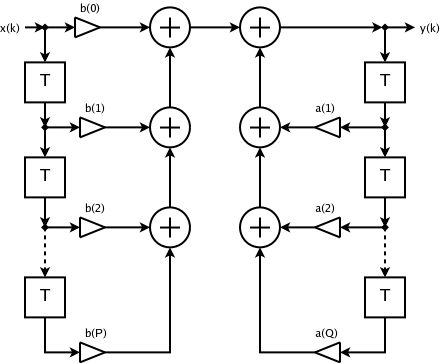
IIR Filter
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |