|
Simplicial Polyhedron
In geometry, a simplicial polytope is a polytope whose facets are all simplices. For example, a ''simplicial polyhedron'' in three dimensions contains only triangular facesPolyhedra, Peter R. Cromwell, 1997. (p.341) and corresponds via Steinitz's theorem to a maximal planar graph. They are topologically dual to simple polytopes. Polytopes which are both simple and simplicial are either simplices or two-dimensional polygons. Examples Simplicial polyhedra include: * Bipyramids * Gyroelongated dipyramids *Deltahedra (equilateral triangles) ** Platonic *** tetrahedron, octahedron, icosahedron ** Johnson solids: ***triangular bipyramid, pentagonal bipyramid, snub disphenoid, triaugmented triangular prism, gyroelongated square dipyramid * Catalan solids: ** triakis tetrahedron, triakis octahedron, tetrakis hexahedron, disdyakis dodecahedron, triakis icosahedron, pentakis dodecahedron, disdyakis triacontahedron Simplicial tilings: * Regular: ** triangular tiling *Laves tilings: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
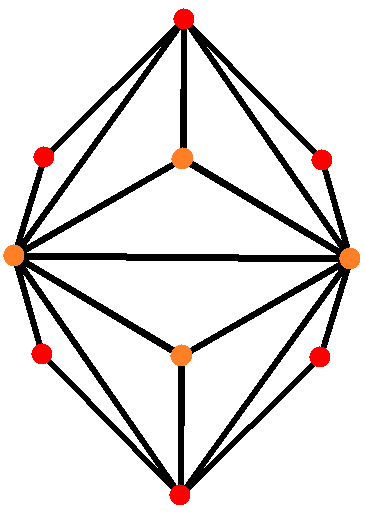
Octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Icosahedron
In geometry, the triakis icosahedron (or kisicosahedronConway, Symmetries of things, p.284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron. Cartesian coordinates Let \phi be the golden ratio. The 12 points given by (0, \pm 1, \pm \phi) and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points (\pm 1, \pm 1, \pm 1) together with the points (\pm\phi, \pm 1/\phi, 0) and cyclic permutations of these coordinates. Multiplying all coordinates of this dodecahedron by a factor of (7\phi-1)/11\approx 0.938\,748\,901\,93 gives a slightly smaller dodecahedron. The 20 vertices of this dodecahedron, together with the vertices of the icosahedron, are the vertices of a triakis icosahedron centered at the origin. The length of its long edges equals 2. Its faces are isosceles triangles with one obtuse angl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disdyakis Dodecahedron
In geometry, a disdyakis dodecahedron, (also hexoctahedron, hexakis octahedron, octakis cube, octakis hexahedron, kisrhombic dodecahedron), is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, and the barycentric subdivision of the cube or of the regular octahedron. The net of the rhombic dodecahedral pyramid also shares the same topology. Symmetry It has Oh octahedral symmetry. Its collective edges represent the reflection planes of the symmetry. It can also be seen in the corner and mid-edge triangulation of the regular cube and octahedron, and rhombic dodecahedron. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube. It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a ''trisoctahedron'', or, more fully, ''trigonal trisoctahedron''. Both names reflect that it has three triangular faces for every face of an octahedron. The ''tetragonal trisoctahedron'' is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron. This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are in different relative distances from the center. If its shorter edges have length 1, its surface area and volume are: :\begin A &= 3\sqrt \\ V &= \frac \end Cartesian coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Tetrahedron
In geometry, a triakis tetrahedron (or kistetrahedron) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron. The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name. The length of the shorter edges is that of the longer edges. If the triakis tetrahedron has shorter edge length 1, it has area and volume . Cartesian coordinates Cartesian coordinates for the 8 vertices of a triakis tetrahedron centered at the origin, are the points (±5/3, ±5/3, ±5/3) with an even number of minus signs, along with the points (±1, ±1, ±1) with an odd numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865. The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic solids and Archimedean solids, the faces of Catalan solids are ''not'' regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Being face-transitive, Catalan solids are isohedron, isohedra. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the Quasiregular polyhedron#Quasiregular duals, duals of the two Quasiregular polyhedron, quasi-regular Archimedean solids. Just as Prism (geometry), prisms and antiprisms are ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Square Dipyramid
In geometry, the gyroelongated square bipyramid, heccaidecadeltahedron, or tetrakis square antiprism is one of the Johnson solids (). As the name suggests, it can be constructed by gyroelongating an octahedron (square bipyramid) by inserting a square antiprism between its congruent halves. It is one of the eight strictly-convex deltahedra. The dual of the gyroelongated square bipyramid is a square truncated trapezohedron with 10 faces: 8 pentagons and 2 square. See also * Gyroelongated bipyramid * Gyroelongated square pyramid In geometry, the gyroelongated square pyramid is one of the Johnson solids (). As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base. ... External links * Johnson solids Deltahedra Pyramids and bipyramids {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triaugmented Triangular Prism
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid. The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. The dual polyhedron of the triaugmented triangular prism is an associahedron, a polyhedron with four quadrilateral faces and six ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snub Disphenoid
In geometry, the snub disphenoid, Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron is a convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight deltahedra (convex polyhedra with equilateral triangle faces), and is the 84th Johnson solid (non-uniform convex polyhedra with regular faces). It can be thought of as a square antiprism where both squares are replaced with two equilateral triangles. The snub disphenoid is also the vertex figure of the isogonal 13-5 step prism, a polychoron constructed from a 13-13 duoprism by selecting a vertex on a tridecagon, then selecting the 5th vertex on the next tridecagon, doing so until reaching the original tridecagon. It cannot be made uniform, however, because the snub disphenoid has no circumscribed sphere. History and naming This shape was called a ''Siamese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Bipyramid
In geometry, the pentagonal bipyramid (or dipyramid) is third of the infinite set of face-transitive bipyramids, and the 13th Johnson solid (). Each bipyramid is the dual of a uniform prism. Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have five faces. Properties If the faces are equilateral triangles, it is a deltahedron and a Johnson solid (''J''13). It can be seen as two pentagonal pyramids (''J''2) connected by their bases. : The pentagonal dipyramid is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.. Formulae The following f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Triaugmented Triangular Prism")
