|
Similarity Learning
Similarity learning is an area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are. It has applications in ranking, in recommendation systems, visual identity tracking, face verification, and speaker verification. Learning setup There are four common setups for similarity and metric distance learning. ; ''Regression similarity learning'' : In this setup, pairs of objects are given (x_i^1, x_i^2) together with a measure of their similarity y_i \in R . The goal is to learn a function that approximates f(x_i^1, x_i^2) \sim y_i for every new labeled triplet example (x_i^1, x_i^2, y_i). This is typically achieved by minimizing a regularized loss \min_W \sum_i loss(w;x_i^1, x_i^2,y_i) + reg(w). ; ''Classification similarity learning'' : Given are pairs of similar objects (x_i, x_i^+) and non similar objects (x_i, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
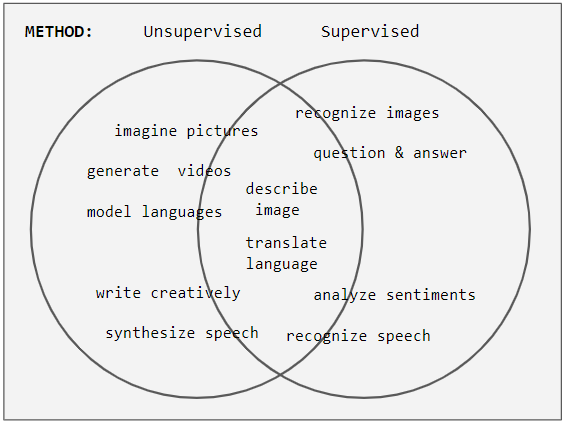
Supervised Learning
Supervised learning (SL) is a machine learning paradigm for problems where the available data consists of labelled examples, meaning that each data point contains features (covariates) and an associated label. The goal of supervised learning algorithms is learning a function that maps feature vectors (inputs) to labels (output), based on example input-output pairs. It infers a function from ' consisting of a set of ''training examples''. In supervised learning, each example is a ''pair'' consisting of an input object (typically a vector) and a desired output value (also called the ''supervisory signal''). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way (see inductive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric (mathematics)
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unsupervised Learning
Unsupervised learning is a type of algorithm that learns patterns from untagged data. The hope is that through mimicry, which is an important mode of learning in people, the machine is forced to build a concise representation of its world and then generate imaginative content from it. In contrast to supervised learning where data is tagged by an expert, e.g. tagged as a "ball" or "fish", unsupervised methods exhibit self-organization that captures patterns as probability densities or a combination of neural feature preferences encoded in the machine's weights and activations. The other levels in the supervision spectrum are reinforcement learning where the machine is given only a numerical performance score as guidance, and semi-supervised learning where a small portion of the data is tagged. Neural networks Tasks vs. methods Neural network tasks are often categorized as discriminative (recognition) or generative (imagination). Often but not always, discriminative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning To Rank
Learning to rank. Slides from Tie-Yan Liu's talk at WWW 2009 conference aravailable online or machine-learned ranking (MLR) is the application of machine learning, typically supervised, semi-supervised or reinforcement learning, in the construction of ranking models for information retrieval systems. Training data consists of lists of items with some partial order specified between items in each list. This order is typically induced by giving a numerical or ordinal score or a binary judgment (e.g. "relevant" or "not relevant") for each item. The goal of constructing the ranking model is to rank new, unseen lists in a similar way to rankings in the training data. Applications In information retrieval Ranking is a central part of many information retrieval problems, such as document retrieval, collaborative filtering, sentiment analysis, and online advertising. A possible architecture of a machine-learned search engine is shown in the accompanying figure. Training ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahalanobis Distance
The Mahalanobis distance is a measure of the distance between a point ''P'' and a distribution ''D'', introduced by P. C. Mahalanobis in 1936. Mahalanobis's definition was prompted by the problem of identifying the similarities of skulls based on measurements in 1927. It is a multi-dimensional generalization of the idea of measuring how many standard deviations away ''P'' is from the mean of ''D''. This distance is zero for ''P'' at the mean of ''D'' and grows as ''P'' moves away from the mean along each principal component axis. If each of these axes is re-scaled to have unit variance, then the Mahalanobis distance corresponds to standard Euclidean distance in the transformed space. The Mahalanobis distance is thus unitless, scale-invariant, and takes into account the correlations of the data set. Definition Given a probability distribution Q on \R^N, with mean \vec = (\mu_1, \mu_2, \mu_3, \dots , \mu_N)^\mathsf and positive-definite covariance matrix S, the Mahalanobis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triplet Loss
Triplet loss is a loss function for machine learning algorithms where a reference input (called anchor) is compared to a matching input (called positive) and a non-matching input (called negative). The distance from the anchor to the positive is minimized, and the distance from the anchor to the negative input is maximized. An early formulation equivalent to triplet loss was introduced (without the idea of using anchors) for metric learning from relative comparisons by M. Schultze and T. Joachims in 2003. By enforcing the order of distances, triplet loss models embed in the way that a pair of samples with same labels are smaller in distance than those with different labels. Unlike t-SNE which preserves embedding orders via probability distributions, triplet loss works directly on embedded distances. Therefore, in its common implementation, it needs soft margin treatment with a slack variable \alpha in its hinge loss-style formulation. It is often used for learning similarity for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Vector
In machine learning and pattern recognition, a feature is an individual measurable property or characteristic of a phenomenon. Choosing informative, discriminating and independent features is a crucial element of effective algorithms in pattern recognition, classification and regression. Features are usually numeric, but structural features such as strings and graphs are used in syntactic pattern recognition. The concept of "feature" is related to that of explanatory variable used in statistical techniques such as linear regression. Classification A numeric feature can be conveniently described by a feature vector. One way to achieve binary classification is using a linear predictor function (related to the perceptron) with a feature vector as input. The method consists of calculating the scalar product between the feature vector and a vector of weights, qualifying those observations whose result exceeds a threshold. Algorithms for classification from a feature vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subadditivity
In mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive functions in various areas of mathematics, particularly norms and square roots. Additive maps are special cases of subadditive functions. Definitions A subadditive function is a function f \colon A \to B, having a domain ''A'' and an ordered codomain ''B'' that are both closed under addition, with the following property: \forall x, y \in A, f(x+y)\leq f(x)+f(y). An example is the square root function, having the non-negative real numbers as domain and codomain, since \forall x, y \geq 0 we have: \sqrt\leq \sqrt+\sqrt. A sequence \left \, n \geq 1, is called subadditive if it satisfies the inequality a_\leq a_n+a_m for all ''m'' and ''n''. This is a special case of subadditive function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |