|
Sill (geostatistics)
In spatial statistics the theoretical variogram, denoted 2\gamma(\mathbf_1,\mathbf_2), is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z(\mathbf). The semivariogram \gamma(\mathbf_1,\mathbf_2) is half the variogram. For example, in gold mining, a variogram will give a measure of how much two samples taken from the mining area will vary in gold percentage depending on the distance between those samples. Samples taken far apart will vary more than samples taken close to each other. Definition The semivariogram \gamma(h) was first defined by Matheron (1963) as half the average squared difference between a function and a translated copy of the function separated at distance h. Formally :\gamma(h)=\frac\iiint_V \left (M+h) - f(M) \right2dM, where M is a point in the geometric field V, and f(M) is the value at that point. The triple integral is over 3 dimensions. h is the separation distance (e.g., in meters or km) of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Statistics ...
Spatial statistics is a field of applied statistics dealing with spatial data. It involves stochastic processes (random fields, point processes), sampling, smoothing and interpolation, regional ( areal unit) and lattice ( gridded) data, point patterns, as well as image analysis and stereology. See also *Geostatistics *Modifiable areal unit problem *Spatial analysis *Spatial econometrics * Statistical geography *Spatial epidemiology * Spatial network * Statistical shape analysis References {{Statistics-stub Applied statistics Statistics Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Size
In mathematics, the cardinality of a finite set is the number of its elements, and is therefore a measure of size of the set. Since the discovery by Georg Cantor, in the late 19th century, of different sizes of infinite sets, the term ''cardinality'' was coined for generalizing to infinite sets the concept of the number of elements. More precisely, two sets have the same cardinality if there exists a one-to-one correspondence between them. In the case of finite sets, the common operation of ''counting'' consists of establishing a one-to-one correspondence between a given set and the set of the first natural numbers, for some natural number . In this case, is the cardinality of the set. A set is ''infinite'' if the counting operation never finishes, that is, if its cardinality is not a natural number. The basic example of an infinite set is the set of all natural numbers. The great discovery of Cantor is that infinite sets of apparently different size may have the same cardina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Difference
The absolute difference of two real numbers x and y is given by , x-y, , the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y, and is a special case of the Lp distance for all 1\le p\le\infty. Its applications in statistics include the absolute deviation from a central tendency. Properties Absolute difference has the following properties: * For x\ge 0, , x-0, =x (zero is the identity element on non-negative numbers) * For all x, , x-x, =0 (every element is its own inverse element) * , x-y, \ge 0 (non-negativity) * , x-y, = 0 if and only if x=y (nonzero for distinct arguments). * , x-y, =, y-x, (''symmetry'' or ''commutativity''). * , x-z, \le, x-y, +, y-z, (the ''triangle inequality''); equality holds if and only if x\le y\le z or x\ge y\ge z. Because it is non-negative, nonzero for distinct arguments, symmetric, and obeys the triangle inequality, the real numbers form a metric space with the absolute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismic Risk
Seismic risk or earthquake risk is the potential impact on the built environment and on people's well-being due to future earthquakes. Seismic risk has been defined, for most management purposes, as the potential economic, social and environmental consequences of hazardous events that may occur in a specified period of time. A building located in a region of high seismic hazard is at lower risk if it is built to sound seismic engineering principles. On the other hand, a building located in a region with a history of minor seismicity, in a brick building located on fill subject to liquefaction can be as high or higher risk. A special subset is urban seismic risk which looks at the specific issues of cities. Risk determination and emergency response can also be determined through the use of an earthquake scenario. Determination of seismic risk The determination of seismic risk is the foundation for risk mitigation decision-making, a key step in risk management. Large corporat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earthquake
An earthquakealso called a quake, tremor, or tembloris the shaking of the Earth's surface resulting from a sudden release of energy in the lithosphere that creates seismic waves. Earthquakes can range in intensity, from those so weak they cannot be felt, to those violent enough to propel objects and people into the air, damage critical infrastructure, and wreak destruction across entire cities. The seismic activity of an area is the frequency, type, and size of earthquakes experienced over a particular time. The seismicity at a particular location in the Earth is the average rate of seismic energy release per unit volume. In its most general sense, the word ''earthquake'' is used to describe any seismic event that generates seismic waves. Earthquakes can occur naturally or be induced by human activities, such as mining, fracking, and nuclear weapons testing. The initial point of rupture is called the hypocenter or focus, while the ground level directly above it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Ground Motion
In seismology, strong ground motion is the strong earthquake shaking that occurs close to (less than about 50 km from) a causative fault. The strength of the shaking involved in strong ground motion usually overwhelms a seismometer, forcing the use of accelerographs (or strong ground motion accelerometers) for recording. The science of strong ground motion also deals with the variations of fault rupture, both in total displacement, energy released, and rupture velocity. As seismic instruments (and accelerometers in particular) become more common, it becomes necessary to correlate expected damage with instrument-readings. The old Modified Mercalli intensity scale (MM), a relic of the pre-instrument days, remains useful in the sense that each intensity-level provides an observable difference in seismic damage. After many years of trying every possible manipulation of accelerometer-time histories, it turns out that the extremely simple peak ground velocity (PGV) provides t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon Dioxide In Earth's Atmosphere
In Earth's atmosphere, carbon dioxide is a trace gas that plays an integral part in the greenhouse effect, carbon cycle, photosynthesis and oceanic carbon cycle. It is one of three main greenhouse gases in the atmosphere of Earth. The concentration of carbon dioxide () in the atmosphere reached 427 ppm (0.0427%) on a molar basis in 2024, representing 3341 gigatonnes of . This is an increase of 50% since the start of the Industrial Revolution, up from 280 ppm during the 10,000 years prior to the mid-18th century. The increase is due to human activity. The current increase in concentrations is primarily driven by the burning of fossil fuels.IPCC (2022Summary for policy makers iClimate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA Other significant human activities that emit include cem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definite
In mathematics, positive definiteness is a property of any object to which a bilinear form In mathematics, a bilinear form is a bilinear map on a vector space (the elements of which are called '' vectors'') over a field ''K'' (the elements of which are called '' scalars''). In other words, a bilinear form is a function that is linea ... or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix * Positive-definite operator * Positive-definite quadratic form References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
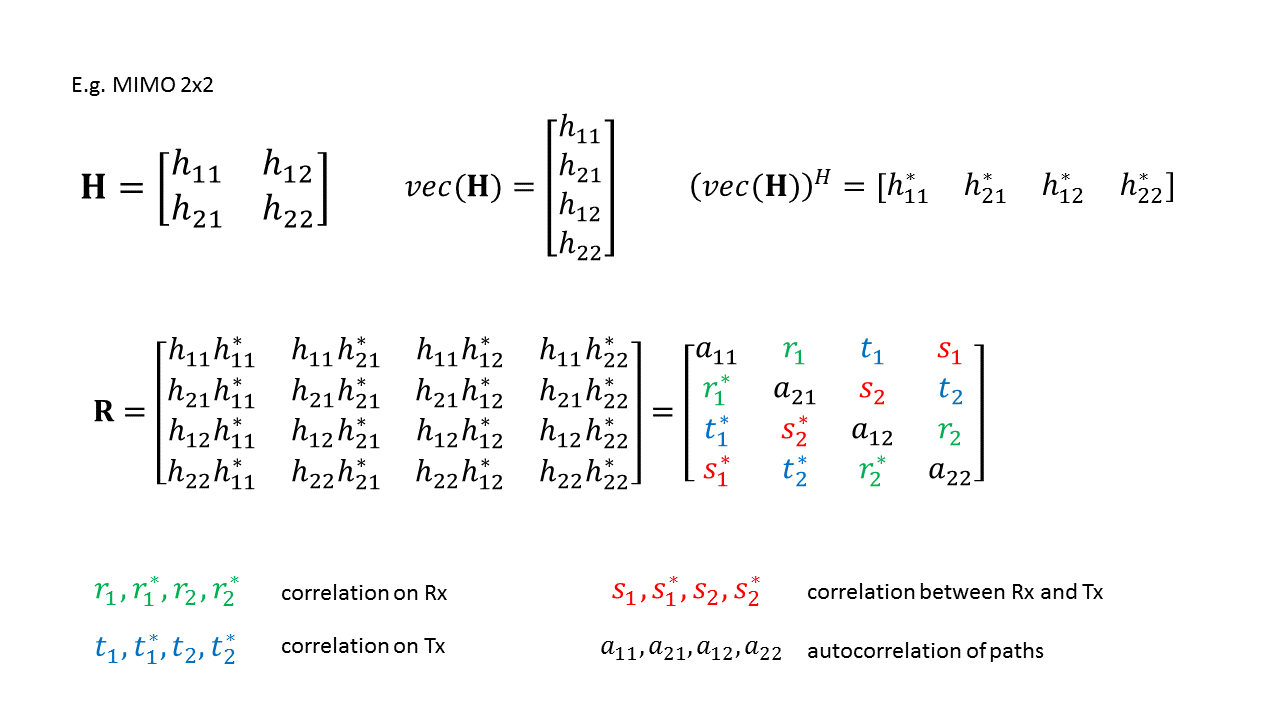
Spatial Correlation
In wireless communication, spatial correlation is the correlation between a signal's spatial direction and the average received signal gain. Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically distributed, then multiple independent channels with identical characteristics can be created by precoding and be used for either transmitting multiple data streams or increasing the reliability (in terms of bit error rate). In practice, the channels between different antennas are often correlated and therefore the potential multi antenna gains may not always be obtainable. Existence In an ideal communication scenario, there is a line-of-sight path between the transmitter and receiver that represents clear spatial channel characteristics. In urban cell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |