|
Signal (model Checking)
In model checking, a subfield of computer science, a signal or timed state sequence is an extension of the notion of words in a formal language, in which letters are continuously emitted. While a word is traditionally defined as a function from a set of non-negative integers to letters, a signal is a function from a set of real numbers to letters. This allow the use of formalisms similar to the ones of automata theory to deal with continuous signals. Example Consider an elevator. What is formally called a letter could be in fact information such as "someone is pressing the button on the 2nd floor", or "the doors are currently open on the third floor". In this case, a signal indicates, at each time, which is the current state of the elevator and its buttons. The signal can then be analyzed using formal methods to check whether a property such that "each time the elevator is called, it arrives in less than three minutes, assuming that no one held the door for more than fifteen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software systems, where the specification contains liveness requirements (such as avoidance of livelock) as well as safety requirements (such as avoidance of states representing a system crash). In order to solve such a problem algorithmically, both the model of the system and its specification are formulated in some precise mathematical language. To this end, the problem is formulated as a task in logic, namely to check whether a structure satisfies a given logical formula. This general concept applies to many kinds of logic and many kinds of structures. A simple model-checking problem consists of verifying whether a formula in the propositional logic is satisfied by a given structure. Overview Property checking is used for verification when two desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to Applied science, practical disciplines (including the design and implementation of Computer architecture, hardware and Computer programming, software). Computer science is generally considered an area of research, academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing Vulnerability (computing), security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Progr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules. The alphabet of a formal language consists of symbols, letters, or tokens that concatenate into strings of the language. Each string concatenated from symbols of this alphabet is called a word, and the words that belong to a particular formal language are sometimes called ''well-formed words'' or ''well-formed formulas''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar, which consists of its formation rules. In computer science, formal languages are used among others as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages in which the words of the language represent concepts that are associated with particular meanings or semantics. In computational complexity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automata Theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word ''automata'' comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments. Automata theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Methods
In computer science, formal methods are mathematically rigorous techniques for the specification, development, and verification of software and hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design. Formal methods employ a variety of theoretical computer science fundamentals, including logic calculi, formal languages, automata theory, control theory, program semantics, type systems, and type theory. Background Semi-Formal Methods are formalisms and languages that are not considered fully “formal”. It defers the task of completing the semantics to a later stage, which is then done either by human interpretation or by interpretation through software like code or test case generators. Taxonomy Formal methods can be used at a number of levels: Level 0: Formal specification may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Temporal Logic
Metric temporal logic (MTL) is a special case of temporal logic. It is an extension of temporal logic in which temporal operators are replaced by time-constrained versions like ''until'', ''next'', ''since'' and ''previous'' operators. It is a linear-time logic that assumes both the interleaving and fictitious-clock abstractions. It is defined over a point-based weakly-monotonic integer-time semantics. MTL has been described as a prominent specification formalism for real-time systems.J. Ouaknine and J. Worrell, "On the decidability of metric temporal logic," 20th Annual IEEE Symposium on Logic in Computer Science (LICS' 05), 2005, pp. 188-197. Full MTL over infinite timed words is undecidable.Ouaknine J., Worrell J. (2006) On Metric Temporal Logic and Faulty Turing Machines. In: Aceto L., Ingólfsdóttir A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2006. Lecture Notes in Computer Science, vol 3921. Springer, Berlin, Heidelberg Syntax The full met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Temporal Logic
In logic, linear temporal logic or linear-time temporal logic (LTL) is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths, e.g., a condition will eventually be true, a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which additionally allows branching time and quantifiers. Subsequently, LTL is sometimes called ''propositional temporal logic'', abbreviated ''PTL''. In terms of expressive power, linear temporal logic (LTL) is a fragment of first-order logic. LTL was first proposed for the formal verification of computer programs by Amir Pnueli in 1977. Syntax LTL is built up from a finite set of propositional variables ''AP'', the logical operators ¬ and ∨, and the temporal modal operators X (some literature uses O or N) and U. Formally, the set of LTL formulas over ''AP'' is inductively defined as follows: * if p ∈ ''AP'' then p is an LTL formula; * if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
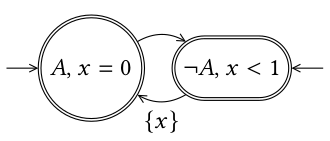
Signal Automaton
In automata theory, a field of computer science, a signal automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a signal automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Example Before formally defining what a signal automaton is, an example will be given. Let one consider the language \mathcal L of signals, over a binary alphabet \, which contains signals \gamma such that: * A appears in singular intervals. That is, the set of times \ is discrete, and * A appears at least once during each interval of length one. This language can be accepted by the automaton pictured nearby. As for finite automaton, incoming arrows represents initial locations and double circle represents acceptin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alphabet (formal Languages)
In formal language theory, an alphabet is a non-empty set of symbol (programming), symbols/glyphs, typically thought of as representing letters, characters, or digits but among other possibilities the "symbols" could also be a set of phonemes (sound units). Alphabets in this technical sense of a set are used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and depending on its purpose maybe be Finite set, finite (e.g., the alphabet of letters "a" through "z"), countable (e.g., \), or even uncountable (e.g., \). String (computer science), Strings, also known as "words", over an alphabet are defined as a sequence of the symbols from the alphabet set. For example, the alphabet of lowercase letters "a" through "z" can be used to form English words like "iceberg" while the alphabet of both upper and lower case letters can also be used to form proper names like "Wikipedia". A common alphabet is , th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timed Word
In model checking, a subfield of computer science, a timed word is an extension of the notion of words, in a formal language, in which each letter is associated with a positive time tag. The sequence of time tag must be non-decreasing, which intuitively means that letters are received. For example, a system receiving a word over a network may associate to each letter the time at which the letter is received. The non-decreasing condition here means that the letters are received in the correct order. A timed language is a set of timed words. Example Consider an elevator. What is formally called a letter is could be in fact an information such that "someone press the button on the 2nd floor", or "the doors opened on the third floor". In this case, a timed word is a sequence of actions taken by the elevators and its users, with time stamps to recall those actions. The timed word can then be analyzed by formal method to check whether a property such that "each time the elevator is cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timed Word
In model checking, a subfield of computer science, a timed word is an extension of the notion of words, in a formal language, in which each letter is associated with a positive time tag. The sequence of time tag must be non-decreasing, which intuitively means that letters are received. For example, a system receiving a word over a network may associate to each letter the time at which the letter is received. The non-decreasing condition here means that the letters are received in the correct order. A timed language is a set of timed words. Example Consider an elevator. What is formally called a letter is could be in fact an information such that "someone press the button on the 2nd floor", or "the doors opened on the third floor". In this case, a timed word is a sequence of actions taken by the elevators and its users, with time stamps to recall those actions. The timed word can then be analyzed by formal method to check whether a property such that "each time the elevator is cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Model Checking")
