|
Sieve Of Eratosthenes
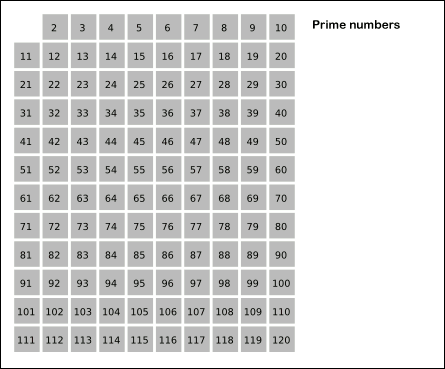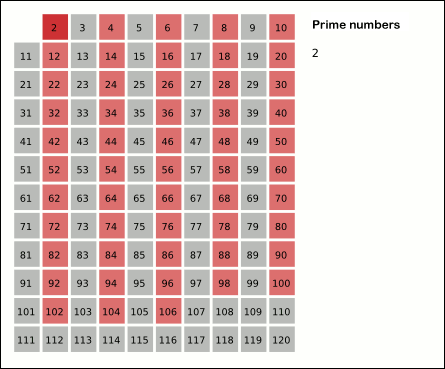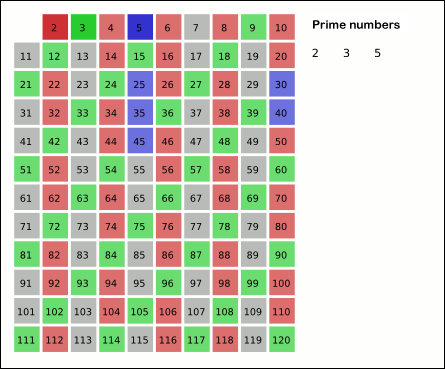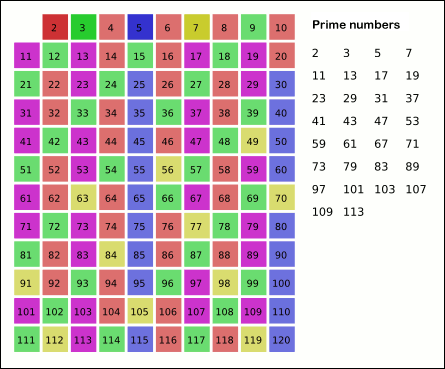
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve ( grc, κόσκινον Ἐρατοσθένους, ''kóskinon Erat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Eratosthenes Animation
A sieve, fine mesh strainer, or sift, is a device for separating wanted elements from unwanted material or for controlling the particle size distribution of a sample, using a screen such as a woven mesh or net or perforated sheet material. The word ''sift'' derives from ''sieve''. In cooking, a sifter is used to separate and break up clumps in dry ingredients such as flour, as well as to aerate and combine them. A strainer (see Colander), meanwhile, is a form of sieve used to separate suspended solids from a liquid by filtration. Industrial strainer Some industrial strainers available are simplex basket strainers, duplex basket strainers, T-strainers and Y-strainers. Simple basket strainers are used to protect valuable or sensitive equipment in systems that are meant to be shut down temporarily. Some commonly used strainers are bell mouth strainers, foot valve strainers, basket strainers. Most processing industries (mainly pharmaceutical, coatings and liquid food indust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Data Type
In computer science, the Boolean (sometimes shortened to Bool) is a data type that has one of two possible values (usually denoted ''true'' and ''false'') which is intended to represent the two truth values of logic and Boolean algebra. It is named after George Boole George Boole (; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher, and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in ..., who first defined an algebraic system of logic in the mid 19th century. The Boolean data type is primarily associated with Conditional (computer programming), conditional statements, which allow different actions by changing control flow depending on whether a programmer-specified Boolean ''condition'' evaluates to true or false. It is a special case of a more general ''logical data type—''logic does not always need to be Boolean (see probabilistic logic). Generali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Of The Euler Product Formula For The Riemann Zeta Function
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis ''Variae observationes circa series infinitas'' (''Various Observations about Infinite Series''), published by St Petersburg Academy in 1737.John Derbyshire (2003), chapter 7, "The Golden Key, and an Improved Prime Number Theorem" The Euler product formula The Euler product formula for the Riemann zeta function reads :\zeta(s) = \sum_^\infty\frac = \prod_ \frac where the left hand side equals the Riemann zeta function: :\zeta(s) = \sum_^\infty\frac = 1+\frac+\frac+\frac+\frac+ \ldots and the product on the right hand side extends over all prime numbers ''p'': :\prod_ \frac = \frac\cdot\frac\cdot\frac\cdot\frac \cdots \frac \cdots Proof of the Euler product formula This sketch of a proof makes use of simple algebra only. This was the method by which Euler originally discovered the formula. There is a certain sieving property that we can use to our advantage: :\zeta(s) = 1+\frac+\fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for ''Ordnung'', meaning the order of approximation. In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; a famous example of such a difference is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates. Big O notation characterizes functions according to their growth rates: d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Complexity
In computer science, the computational complexity or simply complexity of an algorithm is the amount of resources required to run it. Particular focus is given to time complexity, computation time (generally measured by the number of needed elementary operations) and space complexity, memory storage requirements. The complexity of a computational problem, problem is the complexity of the best algorithms that allow solving the problem. The study of the complexity of explicitly given algorithms is called analysis of algorithms, while the study of the complexity of problems is called computational complexity theory. Both areas are highly related, as the complexity of an algorithm is always an upper bound on the complexity of the problem solved by this algorithm. Moreover, for designing efficient algorithms, it is often fundamental to compare the complexity of a specific algorithm to the complexity of the problem to be solved. Also, in most cases, the only thing that is known about the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-polynomial Time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is a polynomial in the ''numeric value'' of the input (the largest integer present in the input)—but not necessarily in the ''length'' of the input (the number of bits required to represent it), which is the case for polynomial time algorithms. Michael R. Garey and David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, 1979. In general, the numeric value of the input is exponential in the input length, which is why a pseudo-polynomial time algorithm does not necessarily run in polynomial time with respect to the input length. An NP-complete problem with known pseudo-polynomial time algorithms is called weakly NP-complete. An NP-complete problem is called strongly NP-complete if it is proven that it cannot be solved by a pseudo-polynomial time algorithm unless . The strong/weak kinds of NP-hardness are defined anal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Harmonic Series
The sum of the reciprocals of all prime numbers diverges; that is: \sum_\frac1p = \frac12 + \frac13 + \frac15 + \frac17 + \frac1 + \frac1 + \frac1 + \cdots = \infty This was proved by Leonhard Euler in 1737, and strengthens Euclid's 3rd-century-BC result that there are infinitely many prime numbers and Nicole Oresme's 14th-century proof of the divergence of the sum of the reciprocals of the integers (harmonic series). There are a variety of proofs of Euler's result, including a lower bound for the partial sums stating that \sum_\frac1p \ge \log \log (n+1) - \log\frac6 for all natural numbers . The double natural logarithm () indicates that the divergence might be very slow, which is indeed the case. See Meissel–Mertens constant. The harmonic series First, we describe how Euler originally discovered the result. He was considering the harmonic series \sum_^\infty \frac = 1 + \frac + \frac + \frac + \cdots = \infty He had already used the following "product formula" to sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Access Machine
In computer science, random-access machine (RAM) is an abstract machine in the general class of register machines. The RAM is very similar to the counter machine but with the added capability of 'indirect addressing' of its registers. Like the counter machine, The RAM has its instructions in the finite-state portion of the machine (the so-called Harvard architecture). The RAM's equivalent of the universal Turing machinewith its program in the registers as well as its datais called the random-access stored-program machine or RASP. It is an example of the so-called von Neumann architecture and is closest to the common notion of a computer. Together with the Turing machine and counter-machine models, the RAM and RASP models are used for computational complexity analysis. Van Emde Boas (1990) calls these three plus the pointer machine "sequential machine" models, to distinguish them from "parallel random-access machine" models. Introduction to the model The concept of a random-acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dataflow Programming
In computer programming, dataflow programming is a programming paradigm that models a program as a directed graph of the data flowing between operations, thus implementing dataflow principles and architecture. Dataflow programming languages share some features of functional languages, and were generally developed in order to bring some functional concepts to a language more suitable for numeric processing. Some authors use the term ''datastream'' instead of '' dataflow'' to avoid confusion with dataflow computing or dataflow architecture, based on an indeterministic machine paradigm. Dataflow programming was pioneered by Jack Dennis and his graduate students at MIT in the 1960s. Considerations Traditionally, a program is modelled as a series of operations happening in a specific order; this may be referred to as sequential, procedural, control flow (indicating that the program chooses a specific path), or imperative programming. The program focuses on commands, in line with the v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Sorenson
A sieve, fine mesh strainer, or sift, is a device for separating wanted elements from unwanted material or for controlling the particle size distribution of a sample, using a screen such as a woven mesh or net or perforated sheet material. The word ''sift'' derives from ''sieve''. In cooking, a sifter is used to separate and break up clumps in dry ingredients such as flour, as well as to aerate and combine them. A strainer (see Colander), meanwhile, is a form of sieve used to separate suspended solids from a liquid by filtration. Industrial strainer Some industrial strainers available are simplex basket strainers, duplex basket strainers, T-strainers and Y-strainers. Simple basket strainers are used to protect valuable or sensitive equipment in systems that are meant to be shut down temporarily. Some commonly used strainers are bell mouth strainers, foot valve strainers, basket strainers. Most processing industries (mainly pharmaceutical, coatings and liquid food indust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
