|
Separation Oracle
A separation oracle (also called a cutting-plane oracle) is a concept in the mathematical theory of convex optimization. It is a method to describe a convex set that is given as an input to an optimization algorithm. Separation oracles are used as input to ellipsoid methods. Definition Let ''K'' be a convex and compact set in R''n''. A strong separation oracle for ''K'' is an oracle (black box) that, given a vector ''y'' in R''n'', returns one of the following: M. Grötschel, L. Lovász, A. Schrijver: ''Geometric Algorithms and Combinatorial Optimization'', Springer, 1988. *Assert that ''y'' is in ''K''. * Find a hyperplane that separates ''y'' from ''K'': a vector a in R''n'', such that a\cdot y > a\cdot x for all ''x'' in ''K''. A strong separation oracle is completely accurate, and thus may be hard to construct. For practical reasons, a weaker version is considered, which allows for small errors in the boundary of ''K'' and the inequalities. Given a small error toleran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
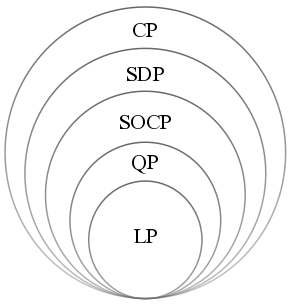
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics (optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Set (graph Theory)
In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set S of vertices such that for every two vertices in S, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in S. A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening. A maximal independent set is an independent set that is not a proper subset of any other independent set. A maximum independent set is an independent set of largest possible size for a given graph G. This size is called the independence number of ''G'' and is usually denoted by \alpha(G). The optimization problem of finding such a set is called the maximum independent set problem. It is a strongly NP-hard problem. As suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computation Oracles
Computation is any type of arithmetic or non-arithmetic calculation that follows a well-defined model (e.g., an algorithm). Mechanical or electronic devices (or, historically, people) that perform computations are known as '' computers''. An especially well-known discipline of the study of computation is computer science. Physical process of Computation Computation can be seen as a purely physical process occurring inside a closed physical system called a computer. Examples of such physical systems are digital computers, mechanical computers, quantum computers, DNA computers, molecular computers, microfluidics-based computers, analog computers, and wetware computers. This point of view has been adopted by the physics of computation, a branch of theoretical physics, as well as the field of natural computing. An even more radical point of view, pancomputationalism (inaudible word), is the postulate of digital physics that argues that the evolution of the universe is itself a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diophantine Approximation
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria. The first problem was to know how well a real number can be approximated by rational numbers. For this problem, a rational number ''a''/''b'' is a "good" approximation of a real number ''α'' if the absolute value of the difference between ''a''/''b'' and ''α'' may not decrease if ''a''/''b'' is replaced by another rational number with a smaller denominator. This problem was solved during the 18th century by means of continued fractions. Knowing the "best" approximations of a given number, the main problem of the field is to find sharp upper and lower bounds of the above difference, expressed as a function of the denominator. It appears that these bounds depend on the nature of the real numbers to be approximated: the lower bound for the approximation of a rational number by another rational number is larger than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid Method
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm which finds an optimal solution in a number of steps that is polynomial in the input size. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function. History The ellipsoid method has a long history. As an iterative method, a preliminary version was introduced by Naum Z. Shor. In 1972, an approximation algorithm for real convex minimization was studied by Arkadi Nemirovski and David B. Yudin (Judin). As an algorithm for solving linear programming problems with rational data, the ellipsoid algorithm was studied by Leonid Khachiyan; Khachiyan's achievement was to prove the polynomial-time solvability of linear programs. This was a notable step from a theoretical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgradient
In mathematics, the subderivative, subgradient, and subdifferential generalize the derivative to convex functions which are not necessarily differentiable. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization. Let f:I \to \mathbb be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function ''f''(''x'')=, ''x'', is nondifferentiable when ''x''=0. However, as seen in the graph on the right (where ''f(x)'' in blue has non-differentiable kinks similar to the absolute value function), for any ''x''0 in the domain of the function one can draw a line which goes through the point (''x''0, ''f''(''x''0)) and which is everywhere either touching or below the graph of ''f''. The slope of such a line is called a ''subderivative'' (because the line is under the graph of ''f''). Definition Rigorously, a ''subder ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigraph (the set of points on or above the graph of the function) is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function x^2 and the exponential function e^x. In simple terms, a convex function refers to a function whose graph is shaped like a cup \cup, while a concave function's graph is shaped like a cap \cap. Convex functions play an important role in many areas of mathematics. They are especially important in the study of optimization problems where they are distinguished by a number of convenient properties. For instance, a strictly convex function on an open set has n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knapsack Problem
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. The problem often arises in resource allocation where the decision-makers have to choose from a set of non-divisible projects or tasks under a fixed budget or time constraint, respectively. The knapsack problem has been studied for more than a century, with early works dating as far back as 1897. The name "knapsack problem" dates back to the early works of the mathematician Tobias Dantzig (1884–1956), and refers to the commonplace problem of packing the most valuable or useful items without overloading the luggage. Applications Knapsack problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bin Packing Problem
The bin packing problem is an optimization problem, in which items of different sizes must be packed into a finite number of bins or containers, each of a fixed given capacity, in a way that minimizes the number of bins used. The problem has many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media and technology mapping in FPGA semiconductor chip design. Computationally, the problem is NP-hard, and the corresponding decision problem - deciding if items can fit into a specified number of bins - is NP-complete. Despite its worst-case hardness, optimal solutions to very large instances of the problem can be produced with sophisticated algorithms. In addition, many approximation algorithms exist. For example, the first fit algorithm provides a fast but often non-optimal solution, involving placing each item into the first bin in which it will fit. It requires '' Θ''(''n'' log ''n'') time, where ''n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Configuration Linear Program
The configuration linear program (configuration-LP) is a particular linear programming used for solving combinatorial optimization problems. It was introduced in the context of the cutting stock problem.Gilmore P. C., R. E. Gomory (1961). A linear programming approach to the cutting-stock problem'. Operations Research 9: 849-859 Later, it has been applied to bin packing and job scheduling. In the configuration-LP, there is a variable for each possible ''configuration'' - each possible multiset of items that can fit in a single bin (these configurations are also known as ''patterns'') . Usually, the number of configurations is exponential in the problem size, but in some cases it is possible to attain approximate solutions using only a polynomial number of configurations. In bin packing The integral LP In the bin packing problem, there are ''n'' items with different sizes. The goal is to pack the items into a minimum number of bins, where each bin can contain at most ''B''. A ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |