|
Sedrakyan's Inequality
The following inequality is known as Sedrakyan's inequality, Bergström's inequality, Engel's form or Titu's lemma, respectively, referring to the article ''About the applications of one useful inequality'' of Nairi Sedrakyan published in 1997, to the book ''Problem-solving strategies'' of Arthur Engel published in 1998 and to the book ''Mathematical Olympiad Treasures'' of Titu Andreescu published in 2003. It is a direct consequence of Cauchy–Bunyakovsky–Schwarz inequality. Nevertheless, in his article (1997) Sedrakyan has noticed that written in this form this inequality can be used as a mathematical proof technique and it has very useful new applications. In the book ''Algebraic Inequalities'' (Sedrakyan) are provided several generalizations of this inequality. Statement of the inequality For any reals a_1, a_2, a_3, \ldots, a_n and positive reals b_1, b_2, b_3,\ldots, b_n, we have \frac + \frac + \cdots + \frac \geq \frac. (Nairi Sedrakyan (1997), Arthur Engel (199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
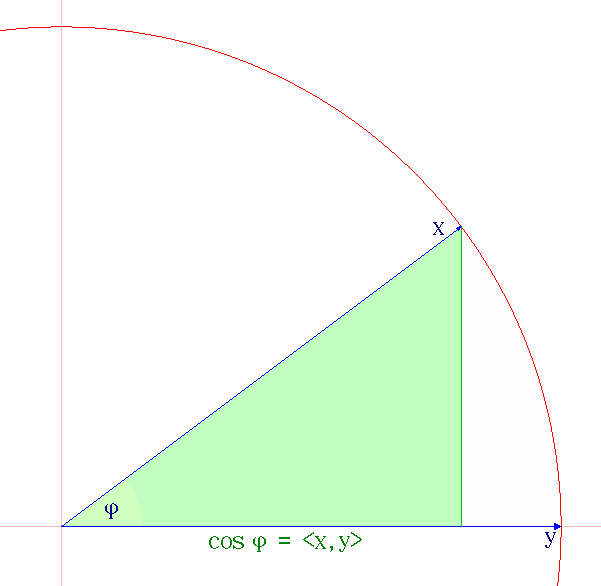
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harald Bergström
Harald Bergström (1 April 1908, Mölltorp – 23 May 2001, Göteborg) was a Swedish mathematician, specializing in probability theory. Education and career Harald Bergström studied mathematics, physics and chemistry at the University of Uppsala and received in 1931 his master's degree. From 1932 to 1934 he taught at secondary schools and then worked as a research assistant at the University of Uppsala; there he received his Ph.D. in 1938 and taught until 1945. In 1946 he moved to Chalmers University of Technology in Göteborg, where in 1949 he was appointed a professor of applied mathematics. In 1960 he was also appointed a professor for numerical analysis and mathematical statistics. In 1974 he retired as professor emeritus. At the University of Uppsala, Harald Bergström did research mainly on algebraic number fields and related topics. After his move to Chalmers University of Technology, he focused on probability theory and statistics. He was supervisor to Peter Jagers. He ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nairi Sedrakyan
Nairi Sedrakyan (born 1961 in Ninotsminda, USSR) is Erdős Award 2022 winner Armenian mathematician involved in national and international Olympiads, including American Mathematics Competitions (USA) and IMO, having been the president of the Armenian Mathematics Olympiads, the Leader of Armenian IMO Team, a jury member and problem selection committee member of the International Mathematical Olympiad, a jury member and problem selection committee member of the Zhautykov International Mathematical Olympiad (IZhO), a jury member and problem selection committee member of the International Olympiad of Metropolises, the president and organizer of the International Mathematical Olympiad Tournament of the Towns in the Republic of Armenia (1986-2013). He has also authored a large number of problems proposed in these Olympiads. The government of Armenia awarded the author the title of the best teacher of Armenia and he received a special gift from the Prime Minister. Nairi Sedrakyan's son ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Engel (mathematician)
Arthur Engel (12 January 1928 – 11 November 2022) was a German mathematics teacher, educationalist and prolific author. His work has been translated into several languages. He had played a role in national and international mathematical competitions since 1970. Engel was one of the first to recognize the impact of electronic calculators and computers on mathematics teaching. He viewed that the focus should shift from learning how to apply algorithms, which could now be done by the machine, to learning how to build and test algorithms. He was also early to see the value of using computers to draw students into an interest and understanding of mathematics. Career Arthur Engel was born in 1928. He graduated from the University of Stuttgart in 1952, and was a secondary school teacher for 18 years. In 1970 he became an associate professor at the Ludwigsburg University of Education, a teacher's training institution. Engel was a Professor of the ''Institut für Didaktik der Mathematik ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Titu Andreescu
Titu Andreescu (born August 19, 1956) is an associate professor of mathematics at the University of Texas at Dallas. He is firmly involved in mathematics contests and olympiads, having been the Director of American Mathematics Competitions (as appointed by the Mathematical Association of America), Director of the Mathematical Olympiad Program, Head Coach of the United States International Mathematical Olympiad Team, and Chairman of the United States of America Mathematical Olympiad. He has also authored a large number of books on the topic of problem solving and olympiad style mathematics. Biography Andreescu was born in the Romanian city of Timișoara in 1956. From an early age, an interest in higher-level mathematics was encouraged by his father and by his uncle Andrew, who was a retired university professor. As a high school student, he excelled in mathematics, and in 1973, 1974, and 1975 won the Romanian national problem solving contests organized by the journal Gazet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variables
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nesbitt's Inequality
In mathematics, Nesbitt's inequality states that for positive real numbers ''a'', ''b'' and ''c'', :\frac+\frac+\frac\geq\frac. It is an elementary special case (N = 3) of the difficult and much studied Shapiro inequality, and was published at least 50 years earlier. There is no corresponding upper bound as any of the 3 fractions in the inequality can be made arbitrarily large. Proof First proof: AM-HM inequality By the AM- HM inequality on (a+b),(b+c),(c+a), :\frac\geq\frac. Clearing denominators yields :((a+b)+(a+c)+(b+c))\left(\frac+\frac+\frac\right)\geq 9, from which we obtain :2\frac+2\frac+2\frac\geq9 by expanding the product and collecting like denominators. This then simplifies directly to the final result. Second proof: Rearrangement Suppose a \ge b \ge c , we have that :\frac 1 \ge \frac 1 \ge \frac 1 define :\vec x = (a, b, c) :\vec y = \left(\frac 1 , \frac 1 , \frac 1 \right) The scalar product of the two sequences is maximum because of the rearrangement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Mathematical Olympiad
The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980. More than 100 countries, representing over 90% of the world's population, send teams of up to six students, plus one team leader, one deputy leader, and observers. The content ranges from extremely difficult algebra and pre-calculus problems to problems on branches of mathematics not conventionally covered in secondary or high school and often not at university level either, such as projective and complex geometry, functional equations, combinatorics, and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions req ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequalities
Inequality may refer to: Economics * Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy * Economic inequality, difference in economic well-being between population groups * Spatial inequality, the unequal distribution of income and resources across geographical regions * Income inequality metrics, used to measure income and economic inequality among participants in a particular economy * International inequality, economic differences between countries Healthcare * Health equity, the study of differences in the quality of health and healthcare across different populations Mathematics * Inequality (mathematics), a relation between two values when they are different Social sciences * Educational inequality, the unequal distribution of academic resources to socially excluded communities * Gender inequality, unequal treatment or perceptions of individuals due to their gender * Participation inequality, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |