|
Sectrix Of Maclaurin
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin (named for Colin Maclaurin), which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them. Equations in polar coordinates We are given two lines rotating about two poles P and P_1. By translation and rotation we may assume P = (0,0) and P_1 = (a, 0). At time t, the line rotating about P has angle \theta = \kappa t + \alpha and the line rotating about P_1 has angle \theta_1 = \kappa_1 t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sectrix Of Maclaurin
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin (named for Colin Maclaurin), which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them. Equations in polar coordinates We are given two lines rotating about two poles P and P_1. By translation and rotation we may assume P = (0,0) and P_1 = (a, 0). At time t, the line rotating about P has angle \theta = \kappa t + \alpha and the line rotating about P_1 has angle \theta_1 = \kappa_1 t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Equations
Parametric may refer to: Mathematics * Parametric equation, a representation of a curve through equations, as functions of a variable *Parametric statistics, a branch of statistics that assumes data has come from a type of probability distribution * Parametric derivative, a type of derivative in calculus *Parametric model, a family of distributions that can be described using a finite number of parameters *Parametric oscillator, a harmonic oscillator whose parameters oscillate in time *Parametric surface, a particular type of surface in the Euclidean space R3 *Parametric family, a family of objects whose definitions depend on a set of parameters Science * Parametric process, in optical physics, any process in which an interaction between light and matter does not change the state of the material *Spontaneous parametric down-conversion, in quantum optics, a source of entangled photon pairs and of single photons *Optical parametric amplifier, a type of laser light source that e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid specified by either the cosine or sine functions with no phase angle that is plotted in polar coordinates. Rose curves or "rhodonea" were named by the Italian mathematician who studied them, Guido Grandi, between the years 1723 and 1728. General overview Specification A rose is the set of points in polar coordinates specified by the polar equation :r=a\cos(k\theta) or in Cartesian coordinates using the parametric equations :x=r\cos(\theta)=a\cos(k\theta)\cos(\theta) :y=r\sin(\theta)=a\cos(k\theta)\sin(\theta). Roses can also be specified using the sine function. Since :\sin(k \theta) = \cos\left( k \theta - \frac \right) = \cos\left( k \left( \theta-\frac \right) \right). Thus, the rose specified by \,r=a\sin(k\theta) is identical to that specified by \,r = a\cos(k\theta) rotated counter-clockwise by \pi/2k radians, which is one-quarter the period of either sinusoid. Since they are specified using the cosine or sin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
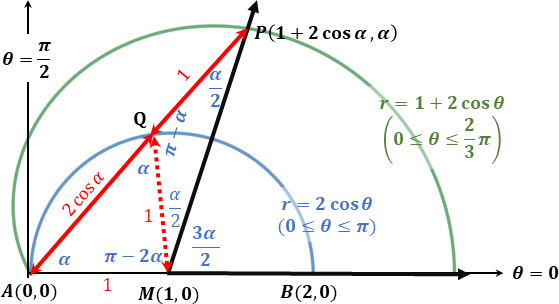
Limaçon Trisectrix
In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin. Specification and loop structure The limaçon trisectrix specified as a polar equation is :r= a(1+2\cos\theta). The constant a may be positive or negative. The two curves with constants a and -a are reflections of each other across the line \theta=\pi/2. The period of r= a(1+2\cos\theta) is 2\pi given the period of the sinusoid \cos\theta. The limaçon trisectrix is composed of two loops. * The outer loop is defined when 1+2\cos\theta\ge0 on the polar angle interval -2\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trisectrix Of Maclaurin
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742. Equations Let two lines rotate about the points P = (0,0) and P_1 = (a, 0) so that when the line rotating about P has angle \theta with the ''x'' axis, the rotating about P_1 has angle 3\theta. Let Q be the point of intersection, then the angle formed by the lines at Q is 2\theta. By the law of sines, : = \! so the equation in polar coordinates is (up to translation and rotation) :r= a \frac = \frac = (4 \cos \theta - \sec \theta)\!. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cassini Oval
In geometry, a Cassini oval is a quartic plane curve defined as the locus (mathematics), locus of points in the plane (geometry), plane such that the Product_(mathematics), product of the distances to two fixed points (Focus (geometry), foci) is constant. This may be contrasted with an ellipse, for which the ''sum'' of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree of a polynomial, degree 2. Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in the late 17th century. Cassini believed that the Sun traveled around the Earth on one of these ovals, with the Earth at one focus of the oval. Other names include Cassinian ovals, Cassinian curves and ovals of Cassini. Formal definition A Cassini oval is a set of points, such that for any point P of the set, the ''product'' of the distances , PP_1, ,\, , PP_2, to two fixed points P_1, P_2 is a consta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonian Circles
In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greek geometer. Definition The Apollonian circles are defined in two different ways by a line segment denoted ''CD''. Each circle in the first family (the blue circles in the figure) is associated with a positive real number ''r'', and is defined as the locus of points ''X'' such that the ratio of distances from ''X'' to ''C'' and to ''D'' equals ''r'', :\left\. For values of ''r'' close to zero, the corresponding circle is close to ''C'', while for values of ''r'' close to ∞, the corresponding circle is close to ''D''; for the intermediate value ''r'' = 1, the circle degenerates to a line, the perpendicular bisector of ''CD''. The equation defining these circles as a locu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Algorithm
In mathematics, the Euclidean algorithm,Some widely used textbooks, such as I. N. Herstein's ''Topics in Algebra'' and Serge Lang's ''Algebra'', use the term "Euclidean algorithm" to refer to Euclidean division or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in Euclid's Elements, his ''Elements'' (c. 300 BC). It is an example of an ''algorithm'', a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce Fraction (mathematics), fractions to their Irreducible fraction, simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compass And Straightedge Constructions
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Curve
In inversive geometry, an inverse curve of a given curve is the result of applying an inverse operation to . Specifically, with respect to a fixed circle with center and radius the inverse of a point is the point for which lies on the ray and . The inverse of the curve is then the locus of as runs over . The point in this construction is called the center of inversion, the circle the circle of inversion, and the radius of inversion. An inversion applied twice is the identity transformation, so the inverse of an inverse curve with respect to the same circle is the original curve. Points on the circle of inversion are fixed by the inversion, so its inverse is itself. Equations The inverse of the point with respect to the unit circle is where :X = \frac,\qquad Y=\frac, or equivalently :x = \frac,\qquad y=\frac. So the inverse of the curve determined by with respect to the unit circle is :f\left(\frac, \frac\right)=0. It is clear from this that inverting an algeb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, \frac \,=\, \frac \,=\, \frac \,=\, 2R, where , and are the lengths of the sides of a triangle, and , and are the opposite angles (see figure 2), while is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the reciprocals; \frac \,=\, \frac \,=\, \frac. The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data (called the ''ambiguous case'') and the technique gives two possible values for the enclosed angle. The law of sines is one of two trigonometric equations commonly a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |