|
Seasonal Variation
In time series data, seasonality is the presence of variations that occur at specific regular intervals less than a year, such as weekly, monthly, or quarterly. Seasonality may be caused by various factors, such as weather, vacation, and holidays and consists of periodic, repetitive, and generally regular and predictable patterns in the levels of a time series. Seasonal fluctuations in a time series can be contrasted with cyclical patterns. The latter occur when the data exhibits rises and falls that are not of a fixed period. Such non-seasonal fluctuations are usually due to economic conditions and are often related to the "business cycle"; their period usually extends beyond a single year, and the fluctuations are usually of at least two years. Organisations facing seasonal variations, such as ice-cream vendors, are often interested in knowing their performance relative to the normal seasonal variation. Seasonal variations in the labour market can be attributed to the entrance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series Analysis
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decade
A decade () is a period of ten years. Decades may describe any ten-year period, such as those of a person's life, or refer to specific groupings of calendar years. Usage Any period of ten years is a "decade". For example, the statement that "during his last decade, Mozart explored chromatic harmony to a degree rare at the time" merely refers to the last ten years of Wolfgang Amadeus Mozart's life without regard to which calendar years are encompassed. Also, 'the first decade' of a person's life begins on the day of their birth and ends at the end of their 10th year of life when they have their 10th birthday; the second decade of life starts with their 11th year of life (during which one is typically still referred to as being "10") and ends at the end of their 20th year of life, on their 20th birthday; similarly, the third decade of life, when one is in one's twenties or 20s, starts with the 21st year of life, and so on, with subsequent decades of life similarly described by ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Season
A season is a division of the year based on changes in weather, ecology, and the number of daylight hours in a given region. On Earth, seasons are the result of the axial parallelism of Earth's tilted orbit around the Sun. In temperate and polar regions, the seasons are marked by changes in the intensity of sunlight that reaches the Earth's surface, variations of which may cause animals to undergo hibernation or to migrate, and plants to be dormant. Various cultures define the number and nature of seasons based on regional variations, and as such there are a number of both modern and historical cultures whose number of seasons varies. The Northern Hemisphere experiences most direct sunlight during May, June, and July, as the hemisphere faces the Sun. The same is true of the Southern Hemisphere in November, December, and January. It is Earth's axial tilt that causes the Sun to be higher in the sky during the summer months, which increases the solar flux. However, due to seas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between gender and income, we could use a dummy variable to represent the gender of each individual in the study. The variable would take on a value of 1 for males and 0 for females. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which would otherwise be difficult to include due to their non-numeric nature. They can also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is consiste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
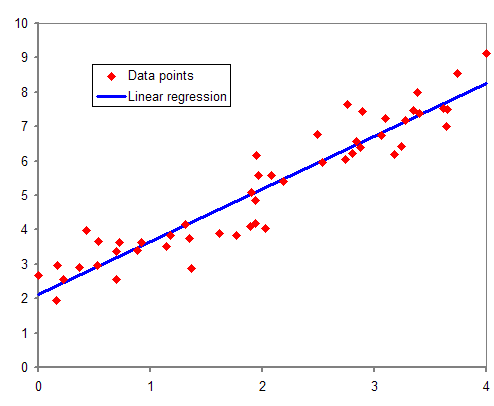
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
X-12-ARIMA
X-13ARIMA-SEATS, successor to X-12-ARIMA and X-11, is a set of statistical methods for seasonal adjustment and other descriptive analysis of time series data that are implemented in the U.S. Census Bureau's software package. These methods are or have been used by Statistics Canada, Australian Bureau of Statistics, and the statistical offices of many other countries. X-12-ARIMA can be used together with many statistical packages, such as SAS in its econometric and time series (ETS) package, R in its (seasonal) package, Gretl or EViews which provides a graphical user interface for X-12-ARIMA, and NumXL which avails X-12-ARIMA functionality in Microsoft Excel. There is also a version for Matlab. Notable statistical agencies presently using X-12-ARIMA for seasonal adjustment include Statistics Canada, the U.S. Bureau of Labor Statistics and Census and Statistics Department (Hong Kong). The Brazilian Institute of Geography and Statistics uses X-13-ARIMA. X-12-ARIMA was the successo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decomposition Of Time Series
The decomposition of time series is a statistical task that deconstructs a time series into several components, each representing one of the underlying categories of patterns. There are two principal types of decomposition, which are outlined below. Decomposition based on rates of change This is an important technique for all types of time series analysis, especially for seasonal adjustment. It seeks to construct, from an observed time series, a number of component series (that could be used to reconstruct the original by additions or multiplications) where each of these has a certain characteristic or type of behavior. For example, time series are usually decomposed into: *T_t, the trend component at time ''t'', which reflects the long-term progression of the series (secular variation). A trend exists when there is a persistent increasing or decreasing direction in the data. The trend component does not have to be linear. *C_t, the cyclical component at time ''t'', which refle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclostationary Process
A cyclostationary process is a signal having statistical properties that vary cyclically with time. A cyclostationary process can be viewed as multiple interleaved stationary processes. For example, the maximum daily temperature in New York City can be modeled as a cyclostationary process: the maximum temperature on July 21 is statistically different from the temperature on December 20; however, it is a reasonable approximation that the temperature on December 20 of different years has identical statistics. Thus, we can view the random process composed of daily maximum temperatures as 365 interleaved stationary processes, each of which takes on a new value once per year. Definition There are two differing approaches to the treatment of cyclostationary processes. The probabilistic approach is to view measurements as an instance of a stochastic process. As an alternative, the deterministic approach is to view the measurements as a single time series, from which a probability distri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |