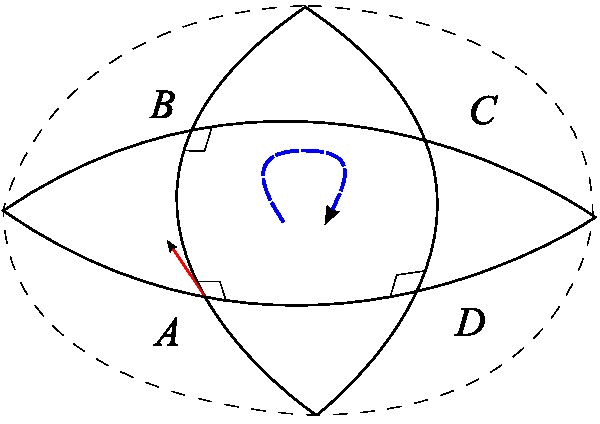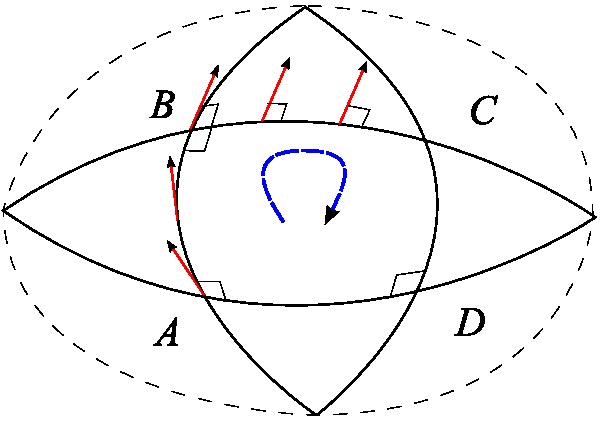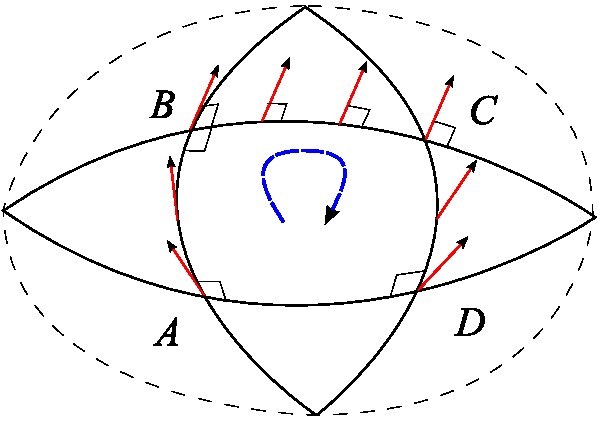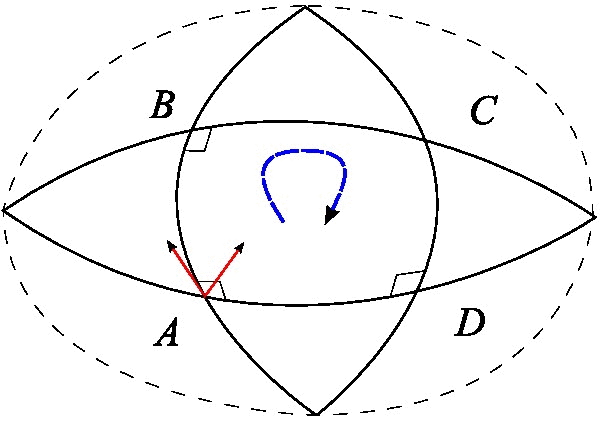
|
Riemann–Christoffel Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tidal Force
The tidal force is a gravitational effect that stretches a body along the line towards the center of mass of another body due to a gradient (difference in strength) in gravitational field from the other body; it is responsible for diverse phenomena, including tides, tidal locking, breaking apart of celestial bodies and formation of ring systems within the Roche limit, and in extreme cases, spaghettification of objects. It arises because the gravitational field exerted on one body by another is not constant across its parts: the nearest side is attracted more strongly than the farthest side. It is this difference that causes a body to get stretched. Thus, the tidal force is also known as the differential force, as well as a secondary effect of the gravitational field. In celestial mechanics, the expression ''tidal force'' can refer to a situation in which a body or material (for example, tidal water) is mainly under the gravitational influence of a second body (for example, the Eart ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariant Derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component (dependent on the embedding) and the intrinsic covariant derivative component. The name is motivated by the importance of changes of coordinate in physics: the covariant derivative transforms covariantly under a general coordinate transformation, that is, linearly via the Jacobia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holonomy
In differential geometry Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multili ..., the holonomy of a connection (mathematics), connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features. Any kind of connection on a manifold gives rise, through its parallel transport maps, to some notion of holonomy. The most common forms of holonomy are for connections possessing some kind of symmetry. Important examples include: holonomy of the Levi-Civit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorema Egregium
Gauss's ''Theorema Egregium'' (Latin for "Remarkable Theorem") is a major result of differential geometry, proved by Carl Friedrich Gauss in 1827, that concerns the curvature of surfaces. The theorem says that Gaussian curvature can be determined entirely by measuring angles, distances and their rates on a surface, without reference to the particular manner in which the surface is embedded in the ambient 3-dimensional Euclidean space. In other words, the Gaussian curvature of a surface does not change if one bends the surface without stretching it. Thus the Gaussian curvature is an intrinsic invariant of a surface. Gauss presented the theorem in this manner (translated from Latin): :Thus the formula of the preceding article leads itself to the remarkable Theorem. If a curved surface is developed upon any other surface whatever, the measure of curvature in each point remains unchanged. The theorem is "remarkable" because the starting ''definition'' of Gaussian curvature mak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a surface at a point is the product of the principal curvatures, and , at the given point: K = \kappa_1 \kappa_2. The Gaussian radius of curvature is the reciprocal of . For example, a sphere of radius has Gaussian curvature everywhere, and a flat plane and a cylinder have Gaussian curvature zero everywhere. The Gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus. Gaussian curvature is an ''intrinsic'' measure of curvature, depending only on distances that are measured “within” or along the surface, not on the way it is isometrically embedding, embedded in Euclidean space. This is the content of the ''Theorema egregium''. Gaussian curvature is named after Carl Friedrich Gauss, who published the ''Theorema egregium'' in 1827. Informal definition At any point on a surface, we can find a Normal (geometry), normal vector that is at right angles to the sur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Transport
In geometry, parallel transport (or parallel translation) is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection (a covariant derivative or connection (vector bundle), connection on the tangent bundle), then this connection allows one to transport vectors of the manifold along curves so that they stay ''parallel'' with respect to the connection. The parallel transport for a connection thus supplies a way of, in some sense, moving the local geometry of a manifold along a curve: that is, of ''connecting'' the geometries of nearby points. There may be many notions of parallel transport available, but a specification of one — one way of connecting up the geometries of points on a curve — is tantamount to providing a ''connection''. In fact, the usual notion of connection is the infinitesimal analog of parallel transport. Or, ''vice versa'', parallel transport is the local realization of a conne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Motivation Shpere
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Biography Early years Riemann was born on 17 September 1826 in Breselenz, a village near Dannenber ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Covariant Derivative
In the math branches of differential geometry and vector calculus, the second covariant derivative, or the second order covariant derivative, of a vector field is the derivative of its derivative with respect to another two tangent vector fields. Definition Formally, given a (pseudo)-Riemannian manifold (''M'', ''g'') associated with a vector bundle ''E'' → ''M'', let ∇ denote the Levi-Civita connection given by the metric ''g'', and denote by Γ(''E'') the space of the smooth sections of the total space ''E''. Denote by ''T*M'' the cotangent bundle of ''M''. Then the second covariant derivative can be defined as the composition of the two ∇s as follows: :\Gamma(E) \stackrel \Gamma(T^*M \otimes E) \stackrel \Gamma(T^*M \otimes T^*M \otimes E). For example, given vector fields ''u'', ''v'', ''w'', a second covariant derivative can be written as :(\nabla^2_ w)^a = u^c v^b \nabla_c \nabla_b w^a by using abstract index notation. It is also straightforward to verify that :(\nabla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrability Condition
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form ''restricts'' to a submanifold, and the fact that this restriction is compatible with the exterior derivative. This is one possible approach to certain over-determined systems, for example, including Lax pair, Lax pairs of Integrable system, integrable systems. A Pfaffian system is specified by 1-forms alone, but the theory includes other types of example of differential system. To elaborate, a Pfaffian system is a set of 1-forms on a smooth manifold (which one sets equal to 0 to find ''solutions'' to the system). Given a collection of differential 1-forms \textstyle\alpha_i, i=1,2,\dots, k on an \textstyle n-dimensional manifold M, an integral manifold is an immersed (not necessarily embedded) submanifold whose t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Bracket Of Vector Fields
In the mathematical field of differential topology, the Lie bracket of vector fields, also known as the Jacobi–Lie bracket or the commutator of vector fields, is an operator that assigns to any two vector fields ''X'' and ''Y'' on a smooth manifold ''M'' a third vector field denoted . Conceptually, the Lie bracket is the derivative of ''Y'' along the flow generated by ''X'', and is sometimes denoted ''\mathcal_X Y'' ("Lie derivative of Y along X"). This generalizes to the Lie derivative of any tensor field along the flow generated by ''X''. The Lie bracket is an R- bilinear operation and turns the set of all smooth vector fields on the manifold ''M'' into an (infinite-dimensional) Lie algebra. The Lie bracket plays an important role in differential geometry and differential topology, for instance in the Frobenius integrability theorem, and is also fundamental in the geometric theory of nonlinear control systems., nonholonomic systems; , feedback linearization. Definitio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |