|
Ranks And Rank Insignia Of The Red Army 1940–1943
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as: Level or position in a hierarchical organization * Academic rank * Diplomatic rank * Hierarchy * Hierarchy of the Catholic Church * Military rank * Police ranks of the United States * Ranking member, S politicsthe most senior member of a committee from the minority party, and thus second-most senior member of a committee * Imperial, royal and noble ranks Level or position in society *Social class *Social position *Social status Places * Rank, Iran, a village * Rank, Nepal, a village development committee People * Rank (surname), a list of people with the name Arts, entertainment, and media Music * ''Rank'' (album), a live album by the Smiths * "Rank", a song by Artwork from '' A Bugged Out Mix'' Other arts, entertainment, and media * Rank (chess), a row of the chessboard * ''Rank'' (film), a short film directed by David Yates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ranking
A ranking is a relationship between a set of items such that, for any two items, the first is either "ranked higher than", "ranked lower than" or "ranked equal to" the second. In mathematics, this is known as a weak order or total preorder of objects. It is not necessarily a total order of objects because two different objects can have the same ranking. The rankings themselves are totally ordered. For example, materials are totally preordered by hardness, while degrees of hardness are totally ordered. If two items are the same in rank it is considered a tie. By reducing detailed measures to a sequence of ordinal numbers, rankings make it possible to evaluate complex information according to certain criteria. Thus, for example, an Internet search engine may rank the pages it finds according to an estimation of their relevance, making it possible for the user quickly to select the pages they are likely to want to see. Analysis of data obtained by ranking commonly requires non-par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (chess)
This glossary of chess explains commonly used terms in chess, in alphabetical order. Some of these terms have their own pages, like ''fork'' and ''pin''. For a list of unorthodox chess pieces, see Fairy chess piece; for a list of terms specific to chess problems, see Glossary of chess problems; for a list of named opening lines, see List of chess openings; for a list of chess-related games, see List of chess variants. A B , "lightning"] A #fast chess, fast form of chess with a very short time limit, usually three or five minutes per player for the entire game. With the advent of electronic chess clocks, the time remaining is often incremented by one or two seconds per move.Schiller 2003, p. 398 C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (type Theory)
In programming languages and type theory, parametric polymorphism allows a single piece of code to be given a "generic" type, using variables in place of actual types, and then instantiated with particular types as needed. Parametrically polymorphic functions and data types are sometimes called generic functions and generic datatypes, respectively, and they form the basis of generic programming. Parametric polymorphism may be contrasted with ad hoc polymorphism. Parametrically polymorphic definitions are ''uniform'': they behave identically regardless of the type they are instantiated at. In contrast, ad hoc polymorphic definitions are given a distinct definition for each type. Thus, ad hoc polymorphism can generally only support a limited number of such distinct types, since a separate implementation has to be provided for each type. Basic definition It is possible to write functions that do not depend on the types of their arguments. For example, the identity function \mathsf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
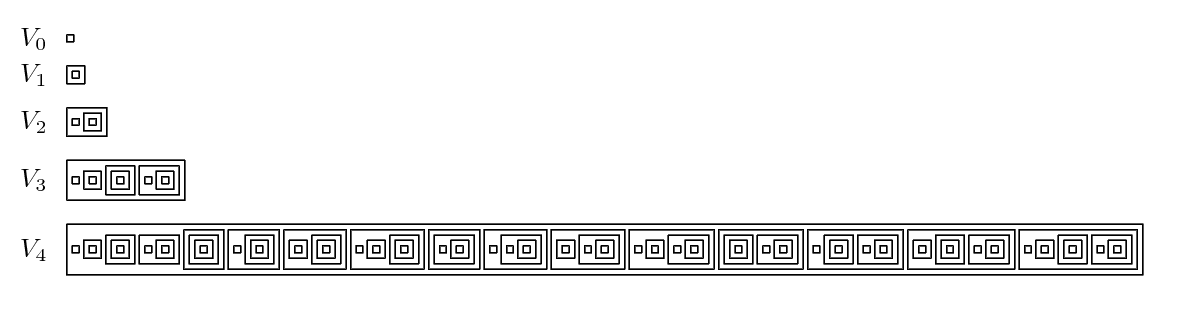
Rank (set Theory)
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (linear Algebra)
In linear algebra, the rank of a matrix is the dimension of the vector space generated (or spanned) by its columns. p. 48, § 1.16 This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the " nondegenerateness" of the system of linear equations and linear transformation encoded by . There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics. The rank is commonly denoted by or ; sometimes the parentheses are not written, as in .Alternative notation includes \rho (\Phi) from and . Main definitions In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see Alternative definitions for several of these. The column rank of is the dimension of the column space of , while the row rank of is the dimension of the row space of . A fundamental result in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (graph Theory)
In graph theory, a branch of mathematics, the rank of an undirected graph has two unrelated definitions. Let equal the number of vertices of the graph. * In the matrix theory of graphs the rank of an undirected graph is defined as the rank of its adjacency matrix. :Analogously, the nullity of the graph is the nullity of its adjacency matrix, which equals . * In the matroid theory of graphs the rank of an undirected graph is defined as the number , where is the number of connected components of the graph. Equivalently, the rank of a graph is the rank of the oriented incidence matrix associated with the graph.. See in particular the discussion on p. 218. :Analogously, the nullity of the graph is the nullity of its oriented incidence matrix, given by the formula , where ''n'' and ''c'' are as above and ''m'' is the number of edges in the graph. The nullity is equal to the first Betti number of the graph. The sum of the rank and the nullity is the number of edges. Examples ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (differential Topology)
In mathematics, the rank of a differentiable map f:M\to N between differentiable manifolds at a point p\in M is the rank of the derivative of f at p. Recall that the derivative of f at p is a linear map :d_p f : T_p M \to T_N\, from the tangent space at ''p'' to the tangent space at ''f''(''p''). As a linear map between vector spaces it has a well-defined rank, which is just the dimension of the image in ''T''''f''(''p'')''N'': :\operatorname(f)_p = \dim(\operatorname(d_p f)). Constant rank maps A differentiable map ''f'' : ''M'' → ''N'' is said to have constant rank if the rank of ''f'' is the same for all ''p'' in ''M''. Constant rank maps have a number of nice properties and are an important concept in differential topology. Three special cases of constant rank maps occur. A constant rank map ''f'' : ''M'' → ''N'' is *an immersion if rank ''f'' = dim ''M'' (i.e. the derivative is everywhere injective), *a submersion if rank ''f'' = dim ''N'' (i.e. the derivative is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memory Rank
A memory rank is a set of DRAM chips connected to the same chip select, which are therefore accessed simultaneously. In practice all DRAM chips share all of the other command and control signals, and only the chip select pins for each rank are separate (the data pins are shared across ranks). Details The term ''rank'' was created and defined by JEDEC, the memory industry standards group. On a DDR, DDR2, or DDR3 memory module, each rank has a 64-bit-wide data bus (72 bits wide on DIMMs that support ECC). The number of physical DRAMs depends on their individual widths. For example, a rank of ×8 (8-bit wide) DRAMs would consist of eight physical chips (nine if ECC is supported), but a rank of ×4 (4-bit wide) DRAMs would consist of 16 physical chips (18, if ECC is supported). Multiple ranks can coexist on a single DIMM, and modern DIMMs can consist of one rank (single rank), two ranks (dual rank), four ranks (quad rank), or eight ranks (octal rank). There is only a little differenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (J Programming Language)
Rank is a generalization of looping as used in scalar (non-array-oriented) programming languages. It is also a generalization of '' mapcar'' in the language ''Lisp'' and ''map'' in modern functional programming languages, and a generalization of scalar extension, inner (matrix) product, and outer product in APL\360. The canonical implementation of rank may be the language '' J'', but it is also available in Dyalog APL, the International Organization for Standardization (ISO) technical standard on Extended APL, and NARS2000. Rank has several different meanings. In general, the concept of ''rank'' is used to treat an orthogonal array in terms of its subarrays. For example, a two-dimensional array may be dealt with at rank 2 as the entire matrix, or at rank 1 to work with its implicit one-dimensional columns or rows, or at rank 0 to work at the level of its individual atoms. *''Noun rank'' – The rank of a noun is a nonnegative integer. *''Verb rank'' – The rank of a verb is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (computer Programming)
In computer programming, rank with no further specifications is usually a synonym for (or refers to) "number of dimensions"; thus, a two-dimensional array has rank ''two'', a three-dimensional array has rank ''three'' and so on. Strictly, no formal definition can be provided which applies to every programming language, since each of them has its own concepts, semantics and terminology; the term may not even be applicable or, to the contrary, applied with a very specific meaning in the context of a given language. In the case of APL the notion applies to every operand; and dyads ("binary functions") have a ''left rank'' and a ''right rank''. The box below instead shows how ''rank of a type'' and ''rank of an array expression'' could be defined (in a semi-formal style) for C++ and illustrates a simple way to calculate them at compile time. #include #include /* Rank of a type * ------------- * * Let the rank of a type T be the number of its dimensions if * it is an array; z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Rank Organisation
The Rank Organisation was a British entertainment conglomerate founded by industrialist J. Arthur Rank in April 1937. It quickly became the largest and most vertically integrated film company in the United Kingdom, owning production, distribution and exhibition facilities. It also diversified into the manufacture of radios, TVs and photocopiers (as one of the owners of Rank Xerox). The company name lasted until February 1996, when the name and some of the remaining assets were absorbed into the newly structured Rank Group plc. The company itself became a wholly owned subsidiary of Xerox and was renamed XRO Limited in 1997. The company logo, the Gongman, first used in 1935 by the group's distribution company General Film DistributorsThe Independent July 16, 199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Rank Group
The Rank Group is a gambling company based in the United Kingdom. Rank was involved in the cinema and motion picture industry until 2006, and continues to use the Gongman logo originally used by the Rank Organisation's film distribution subsidiary General Film Distributors. Its brands now include Mecca Bingo, and Grosvenor Casinos, the UK's largest casino operator. Rank's principal market and headquarters are in the United Kingdom, where it operates Grosvenor Casinos (56 casinos), Mecca Bingo (96 bingo clubs) and Rank Interactive (online gaming and betting). It also operates additional Grosvenor Casinos clubs in Belgium (two casinos), and Rank España in Spain (10 bingo clubs). Rank is listed on the London Stock Exchange. History The company was formed to acquire the business interests of the Rank Organisation, which itself was formed out of the business interests of its founder, J. Arthur Rank. Until the start of the 21st century, the group still had a tremendous amount of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |