|
Round-off Errors
A roundoff error, also called rounding error, is the difference between the result produced by a given algorithm using exact arithmetic and the result produced by the same algorithm using finite-precision, rounded arithmetic. Rounding errors are due to inexactness in the representation of real numbers and the arithmetic operations done with them. This is a form of quantization error. When using approximation equations or algorithms, especially when using finitely many digits to represent real numbers (which in theory have infinitely many digits), one of the goals of numerical analysis is to estimate computation errors. Computation errors, also called numerical errors, include both truncation errors and roundoff errors. When a sequence of calculations with an input involving any roundoff error are made, errors may accumulate, sometimes dominating the calculation. In ill-conditioned problems, significant error may accumulate. In short, there are two major facets of roundoff errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guard Digit
In numerical analysis, one or more guard digits can be used to reduce the amount of roundoff error. For example, suppose that the final result of a long, multi-step calculation can be safely rounded off to ''N'' decimal places. That is to say, the roundoff error introduced by this final roundoff makes a negligible contribution to the overall uncertainty. However, it is quite likely that it is ''not'' safe to round off the intermediate steps in the calculation to the same number of digits. Be aware that roundoff errors can accumulate. If ''M'' decimal places are used in the intermediate calculation, we say there are ''M−N'' guard digits. Guard digits are also used in floating point operations in most computer systems. Given 2^1 \times 0.100_2 - 2^0 \times 0.111_2 we have to line up the binary points. This means we must add an extra digit to the first operand—a guard digit. This gives us 2^1 \times 0.1000_2 - 2^1 \times 0.0111_2. Performing this operation gives us 2^1 \tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
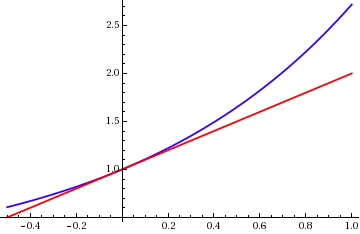
Catastrophic Cancellation
In numerical analysis, catastrophic cancellation is the phenomenon that subtracting good approximations to two nearby numbers may yield a very bad approximation to the difference of the original numbers. For example, if there are two studs, one L_1 = 254.5\,\text long and the other L_2 = 253.5\,\text long, and they are measured with a ruler that is good only to the centimeter, then the approximations could come out to be \tilde L_1 = 255\,\text and \tilde L_2 = 253\,\text. These may be good approximations, in relative error, to the true lengths: the approximations are in error by less than 2% of the true lengths, , L_1 - \tilde L_1, /, L_1, < 2\%. However, if the ''approximate'' lengths are subtracted, the difference will be , even though the true difference between the lengths is . The difference of the approximations, |
Florida
Florida is a state located in the Southeastern region of the United States. Florida is bordered to the west by the Gulf of Mexico, to the northwest by Alabama, to the north by Georgia, to the east by the Bahamas and Atlantic Ocean, and to the south by the Straits of Florida and Cuba; it is the only state that borders both the Gulf of Mexico and the Atlantic Ocean. Spanning , Florida ranks 22nd in area among the 50 states, and with a population of over 21 million, it is the third-most populous. The state capital is Tallahassee, and the most populous city is Jacksonville. The Miami metropolitan area, with a population of almost 6.2 million, is the most populous urban area in Florida and the ninth-most populous in the United States; other urban conurbations with over one million people are Tampa Bay, Orlando, and Jacksonville. Various Native American groups have inhabited Florida for at least 14,000 years. In 1513, Spanish explorer Juan Ponce de León became the first k ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boca Raton
Boca Raton ( ; es, Boca Ratón, link=no, ) is a city in Palm Beach County, Florida, United States. It was first incorporated on August 2, 1924, as "Bocaratone," and then incorporated as "Boca Raton" in 1925. The population was 97,422 in the 2020 census, and it was ranked as the 344th largest city in America in 2022. However, approximately 200,000 additional people with a Boca Raton postal address live outside of municipal boundaries, such as in West Boca Raton. As a business center, the city experiences significant daytime population increases. Boca Raton is north of Miami and is a principal city of the Miami metropolitan area, which had a population of 6,012,331 as of 2015. Boca Raton is home to the main campus of Florida Atlantic University and the corporate headquarters of Office Depot. It is also home to the Evert Tennis Academy, owned by former professional tennis player Chris Evert. Boca Town Center, an upscale shopping center in central Boca Raton, is one of the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Epsilon
Machine epsilon or machine precision is an upper bound on the relative approximation error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science. The quantity is also called macheps and it has the symbols Greek epsilon \varepsilon. There are two prevailing definitions. In numerical analysis, machine epsilon is dependent on the type of rounding used and is also called unit roundoff, which has the symbol bold Roman u. However, by a less formal, but more widely-used definition, machine epsilon is independent of rounding method and may be equivalent to u or 2u. Values for standard hardware arithmetics The following table lists machine epsilon values for standard floating-point formats. Each format uses round-to-nearest. Formal definition ''Rounding'' is a procedure for choosing the representation of a real number in a floating point number system. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rounding
Rounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $ with $, the fraction 312/937 with 1/3, or the expression with . Rounding is often done to obtain a value that is easier to report and communicate than the original. Rounding can also be important to avoid misleadingly precise reporting of a computed number, measurement, or estimate; for example, a quantity that was computed as but is known to be accurate only to within a few hundred units is usually better stated as "about ". On the other hand, rounding of exact numbers will introduce some round-off error in the reported result. Rounding is almost unavoidable when reporting many computations – especially when dividing two numbers in integer or fixed-point arithmetic; when computing mathematical functions such as square roots, logarithms, and sines; or when using a floating-point representation with a fixed number of significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Institute Of Electrical And Electronics Engineers
The Institute of Electrical and Electronics Engineers (IEEE) is a 501(c)(3) professional association for electronic engineering and electrical engineering (and associated disciplines) with its corporate office in New York City and its operations center in Piscataway, New Jersey. The mission of the IEEE is ''advancing technology for the benefit of humanity''. The IEEE was formed from the amalgamation of the American Institute of Electrical Engineers and the Institute of Radio Engineers in 1963. Due to its expansion of scope into so many related fields, it is simply referred to by the letters I-E-E-E (pronounced I-triple-E), except on legal business documents. , it is the world's largest association of technical professionals with more than 423,000 members in over 160 countries around the world. Its objectives are the educational and technical advancement of electrical and electronic engineering, telecommunications, computer engineering and similar disciplines. History Origins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floating-point Arithmetic
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number: 12.345 = \underbrace_\text \times \underbrace_\text\!\!\!\!\!\!^ In practice, most floating-point systems use base two, though base ten (decimal floating point) is also common. The term ''floating point'' refers to the fact that the number's radix point can "float" anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating point can be considered a form of scientific notation. A floating-point system can be used to represent, with a fixed number of digits, numbers of very different orders of magnitude — such as the number of meters between galaxies or between protons in an atom. For this reason, floating-poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed-point Arithmetic
In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar amounts, for example, are often stored with exactly two fractional digits, representing the cents (1/100 of dollar). More generally, the term may refer to representing fractional values as integer multiples of some fixed small unit, e.g. a fractional amount of hours as an integer multiple of ten-minute intervals. Fixed-point number representation is often contrasted to the more complicated and computationally demanding floating-point representation. In the fixed-point representation, the fraction is often expressed in the same number base as the integer part, but using negative powers of the base ''b''. The most common variants are decimal (base 10) and binary (base 2). The latter is commonly known also as binary scaling. Thus, if ''n'' fraction digits are stored, the value will always be an integer multiple of ''b' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double-precision Floating-point Format
Double-precision floating-point format (sometimes called FP64 or float64) is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point. Floating point is used to represent fractional values, or when a wider range is needed than is provided by fixed point (of the same bit width), even if at the cost of precision. Double precision may be chosen when the range or precision of single precision would be insufficient. In the IEEE 754-2008 standard, the 64-bit base-2 format is officially referred to as binary64; it was called double in IEEE 754-1985. IEEE 754 specifies additional floating-point formats, including 32-bit base-2 ''single precision'' and, more recently, base-10 representations. One of the first programming languages to provide single- and double-precision floating-point data types was Fortran. Before the widespread adoption of IEEE 754-1985, the representation and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
