|
Ronald A Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the modern synthesis. For his contributions to biology, Fisher has been called "the greatest of Darwin’s successors". Fisher held strong views on race and eugenics, insisting on racial differences. Although he was clearly a eugenist and advocated for the legalization of voluntary sterilization of those with heritable mental disabilities, there is some debate as to whether Fisher supported ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adelaide
Adelaide ( ) is the capital city of South Australia, the state's largest city and the fifth-most populous city in Australia. "Adelaide" may refer to either Greater Adelaide (including the Adelaide Hills) or the Adelaide city centre. The demonym ''Adelaidean'' is used to denote the city and the residents of Adelaide. The Traditional Owners of the Adelaide region are the Kaurna people. The area of the city centre and surrounding parklands is called ' in the Kaurna language. Adelaide is situated on the Adelaide Plains north of the Fleurieu Peninsula, between the Gulf St Vincent in the west and the Mount Lofty Ranges in the east. Its metropolitan area extends from the coast to the foothills of the Mount Lofty Ranges, and stretches from Gawler in the north to Sellicks Beach in the south. Named in honour of Queen Adelaide, the city was founded in 1836 as the planned capital for the only freely-settled British province in Australia. Colonel William Light, one of Adelaide's foun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Principle
Fisher's principle is an evolutionary model that explains why the sex ratio of most species that produce offspring through sexual reproduction is approximately 1:1 between males and females. A. W. F. Edwards has remarked that it is "probably the most celebrated argument in evolutionary biology". Fisher's principle was outlined by Ronald Fisher in his 1930 book ''The Genetical Theory of Natural Selection'' (but has been incorrectly attributed as original to Fisher). Fisher couched his argument in terms of parental expenditure, and predicted that parental expenditure on both sexes should be equal. Sex ratios that are 1:1 are hence known as "", and those that are ''not'' 1:1 are "" or "" and occur because they break the assumptions made in Fisher's model.Charnov, E., and Bull, J. (1989).Non-fisherian sex ratios with sex change and environmental sex determination, ''Nature 338,'' pp. 148–150. https://doi.org/10.1038/338148a0 Retrieved 29 March 2022. Basic explanation W.D. Hamilton g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or F-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definition The F-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of : X = \frac where S_1 and S_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by : \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is well-define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Consistency
In statistics, Fisher consistency, named after Ronald Fisher, is a desirable property of an estimator asserting that if the estimator were calculated using the entire population rather than a sample, the true value of the estimated parameter would be obtained. Definition Suppose we have a statistical sample ''X''1, ..., ''X''''n'' where each ''X''''i'' follows a cumulative distribution ''F''''θ'' which depends on an unknown parameter ''θ''. If an estimator of ''θ'' based on the sample can be represented as a functional of the empirical distribution function ''F̂n'': :\hat =T(\hat F_n) \,, the estimator is said to be ''Fisher consistent'' if: :T(F_\theta) = \theta \, . As long as the ''X''''i'' are exchangeable, an estimator ''T'' defined in terms of the ''X''''i'' can be converted into an estimator ''T′'' that can be defined in terms of ''F̂n'' by averaging ''T'' over all permutations of the data. The resulting estimator will have the same expected value as ''T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Transformation
In statistics, the Fisher transformation (or Fisher ''z''-transformation) of a Pearson correlation coefficient is its inverse hyperbolic tangent (artanh). When the sample correlation coefficient ''r'' is near 1 or -1, its distribution is highly Skewness, skewed, which makes it difficult to estimate confidence intervals and apply tests of significance for the population correlation coefficient ρ. The Fisher transformation solves this problem by yielding a variable whose distribution is approximately normally distributed, with a variance that is stable over different values of ''r''. Definition Given a set of ''N'' bivariate sample pairs (''X''''i'', ''Y''''i''), ''i'' = 1, …, ''N'', the Pearson product-moment correlation coefficient, sample correlation coefficient ''r'' is given by :r = \frac = \frac. Here \operatorname(X,Y) stands for the covariance between the variables X and Y and \sigma stands for the standard deviation of the respective var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Z-distribution
Fisher's ''z''-distribution is the statistical distribution of half the logarithm of an ''F''-distribution variate: : z = \frac 1 2 \log F It was first described by Ronald Fisher in a paper delivered at the International Mathematical Congress of 1924 in Toronto. Nowadays one usually uses the ''F''-distribution instead. The probability density function and cumulative distribution function can be found by using the ''F''-distribution at the value of x' = e^ \, . However, the mean and variance do not follow the same transformation. The probability density function is : f(x; d_1, d_2) = \frac \frac, where ''B'' is the beta function. When the degrees of freedom Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ... becomes large (d_1, d_2 \rightarrow \infty) the distribution appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Noncentral Hypergeometric Distribution
In probability theory and statistics, Fisher's noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where sampling probabilities are modified by weight factors. It can also be defined as the conditional distribution of two or more binomially distributed variables dependent upon their fixed sum. The distribution may be illustrated by the following urn model. Assume, for example, that an urn contains ''m''1 red balls and ''m''2 white balls, totalling ''N'' = ''m''1 + ''m''2 balls. Each red ball has the weight ω1 and each white ball has the weight ω2. We will say that the odds ratio is ω = ω1 / ω2. Now we are taking balls randomly in such a way that the probability of taking a particular ball is proportional to its weight, but independent of what happens to the other balls. The number of balls taken of a particular color follows the binomial distribution. If the total number ''n'' of balls taken is known then the conditional distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Fundamental Theorem Of Natural Selection
Fisher's fundamental theorem of natural selection is an idea about genetic variance in population genetics developed by the statistician and evolutionary biologist Ronald Fisher. The proper way of applying the abstract mathematics of the theorem to actual biology has been a matter of some debate. It states: :"The rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time." Or in more modern terminology: :"The rate of increase in the mean fitness of any organism, at any time, that is ascribable to natural selection acting through changes in gene frequencies, is exactly equal to its genetic variance in fitness at that time". History The theorem was first formulated in Fisher's 1930 book ''The Genetical Theory of Natural Selection''. Fisher likened it to the law of entropy in physics, stating that "It is not a little instructive that so similar a law should hold the supreme position among the biological sciences". The model of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisherian Runaway
Fisherian runaway or runaway selection is a sexual selection mechanism proposed by the mathematical biologist Ronald Fisher in the early 20th century, to account for the evolution of ostentatious male ornamentation by persistent, directional female choice. An example is the colourful and elaborate peacock plumage compared to the relatively subdued peahen plumage; the costly ornaments, notably the bird's extremely long tail, appear to be incompatible with natural selection. Fisherian runaway can be postulated to include sexually dimorphic phenotypic traits such as behavior expressed by a particular sex. Extreme and (seemingly) maladaptive sexual dimorphism represented a paradox for evolutionary biologists from Charles Darwin's time up to the modern synthesis. Darwin attempted to resolve the paradox by assuming heredity for both the preference and the ornament, and supposed an "aesthetic sense" in higher animals, leading to powerful selection of both characteristics in subsequent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Method
In statistics, Fisher's method, also known as Fisher's combined probability test, is a technique for data fusion or "meta-analysis" (analysis of analyses). It was developed by and named for Ronald Fisher. In its basic form, it is used to combine the results from several independence tests bearing upon the same overall hypothesis (''H''0). Application to independent test statistics Fisher's method combines extreme value probabilities from each test, commonly known as "p-values", into one test statistic (''X''2) using the formula :X^2_ \sim -2\sum_^k \log(p_i), where ''p''''i'' is the p-value for the ''i''th hypothesis test. When the p-values tend to be small, the test statistic ''X''2 will be large, which suggests that the null hypotheses are not true for every test. When all the null hypotheses are true, and the ''p''''i'' (or their corresponding test statistics) are independent, ''X''2 has a chi-squared distribution with 2''k'' degrees of freedom, where ''k'' is the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Information
In mathematical statistics, the Fisher information (sometimes simply called information) is a way of measuring the amount of information that an observable random variable ''X'' carries about an unknown parameter ''θ'' of a distribution that models ''X''. Formally, it is the variance of the score, or the expected value of the observed information. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior (according to the Bernstein–von Mises theorem, which was anticipated by Laplace for exponential families). The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized by the statistician Ronald Fisher (following some initial results by Francis Ysidro Edgeworth). The Fisher information is also used in the calculation of the Jeffreys prior, which is used in Bayesian statistics. The Fisher information matrix is used to calculate the covariance matrices associat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
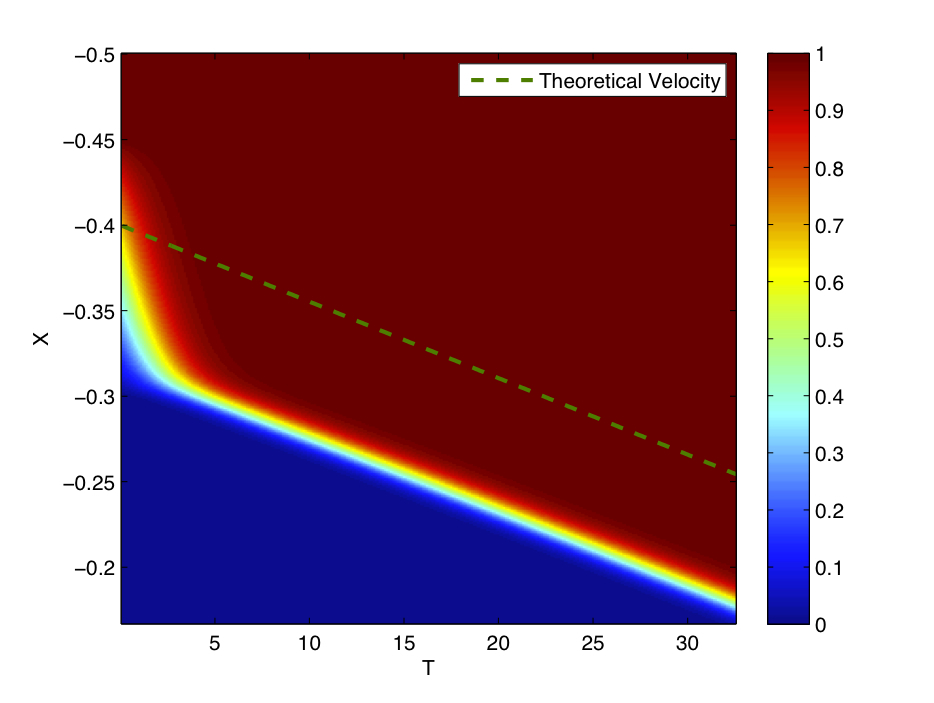
Fisher's Equation
In mathematics, Fisher's equation (named after statistician and biologist Ronald Fisher) also known as the Kolmogorov–Petrovsky–Piskunov equation (named after Andrey Kolmogorov, Ivan Petrovsky, and Nikolai Piskunov), KPP equation or Fisher–KPP equation is the partial differential equation: : \frac - D \frac = r u(1-u).\, It is a kind of reaction–diffusion system that can be used to model population growth and wave propagation. Details Fisher's equation belongs to the class of reaction–diffusion equation: in fact, it is one of the simplest semilinear reaction-diffusion equations, the one which has the inhomogeneous term : f(u,x,t) = r u (1-u),\, which can exhibit traveling wave solutions that switch between equilibrium states given by f(u) = 0. Such equations occur, e.g., in ecology, physiology, combustion, crystallization, plasma physics, and in general phase transition problems. Fisher proposed this equation in his 1937 paper ''The wave of advance of advanta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |