|
Ring Of Periods
In algebraic geometry, a period is a number that can be expressed as an integral of an algebraic function over an algebraic domain. Sums and products of periods Closure (mathematics), remain periods, so the periods form a ring (mathematics), ring. Maxim Kontsevich and Don Zagier gave a survey of periods and introduced some conjectures about them. Periods also arise in computing the integrals that arise from Feynman diagram, Feynman diagrams, and there has been intensive work trying to understand the connections. Definition A real number is a period if it is of the form \int_Q(x,y,z,\ldots) \mathrmx\mathrmy\mathrmz\ldots where P is a polynomial and Q a rational function on \mathbb^n with rational coefficients. A complex number is a period if its real and imaginary parts are periods. An alternative definition allows P and Q to be algebraic function, algebraic functions; this looks more general, but is equivalent. The coefficients of the rational functions and polynomials c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros. The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscates and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M \ (z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Change Of Variables
Change or Changing may refer to: Alteration * Impermanence, a difference in a state of affairs at different points in time * Menopause, also referred to as "the change", the permanent cessation of the menstrual period * Metamorphosis, or change, a biological process by which an animal physically develops after birth or hatching * Personal development, or personal change, activities that improve awareness and identity * Social change, an alteration in the social order of a society * Technological change, invention, innovation, and diffusion of technology Organizations and politics * Change 2011, a Finnish political party * Change We Need, a slogan for Barack Obama's 2008 presidential campaign * Change.gov, the transition website for the incoming Obama administration in 2008–2009 * Change.org, a petition website operated by Change.org, Inc. * Communities Helping All Neighbors Gain Empowerment (CHANGE), a civic organization based in Winston-Salem, North Carolina * Movement for C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation, in contrast to an algebraic function. In other words, a transcendental function "transcends" algebra in that it cannot be expressed algebraically. Examples of transcendental functions include the exponential function, the logarithm, and the trigonometric functions. Definition Formally, an analytic function ''f''(''z'') of one real or complex variable ''z'' is transcendental if it is algebraically independent of that variable. This can be extended to functions of several variables. History The transcendental functions sine and cosine were tabulated from physical measurements in antiquity, as evidenced in Greece (Hipparchus) and India ( jya and koti-jya). In describing Ptolemy's table of chords, an equivalent to a table of sines, Olaf Pedersen wrote: A revolutionary understanding of these circular functions occurred in the 17th century and was explicated by Leonhard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definable Number
Informally, a definable real number is a real number that can be uniquely specified by its description. The description may be expressed as a construction or as a formula of a formal language. For example, the positive square root of 2, \sqrt, can be defined as the unique positive solution to the equation x^2 = 2, and it can be constructed with a compass and straightedge. Different choices of a formal language or its interpretation give rise to different notions of definability. Specific varieties of definable numbers include the constructible numbers of geometry, the algebraic numbers, and the computable numbers. Because formal languages can have only countably many formulas, every notion of definable numbers has at most countably many definable real numbers. However, by Cantor's diagonal argument, there are uncountably many real numbers, so almost every real number is undefinable. Constructible numbers One way of specifying a real number uses geometric techniques. A real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computable Number
In mathematics, computable numbers are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm. They are also known as the recursive numbers, effective numbers or the computable reals or recursive reals. Equivalent definitions can be given using μ-recursive functions, Turing machines, or λ-calculus as the formal representation of algorithms. The computable numbers form a real closed field and can be used in the place of real numbers for many, but not all, mathematical purposes. Informal definition using a Turing machine as example In the following, Marvin Minsky defines the numbers to be computed in a manner similar to those defined by Alan Turing in 1936; i.e., as "sequences of digits interpreted as decimal fractions" between 0 and 1: The key notions in the definition are (1) that some ''n'' is specified at the start, (2) for any ''n'' the computation only takes a finite number of steps, after which the machine produces the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Constant
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory, statistics, and calculus. What it means for a constant to arise "naturally", and what makes a constant "interesting", is ultimately a matter of taste, with some mathematical constants being notable more for historical reasons than for their intrinsic mathematical interest. The more popular constants have been studied throughout the ages and computed to many decimal places. All named mathematical constants are definable numbers, and usually are also computable numbers (Chaitin's constant being a significant exception). Basic mathematical constants These are constants which one is likely to encounter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Numbers
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and . Though only a few classes of transcendental numbers are known—partly because it can be extremely difficult to show that a given number is transcendental—transcendental numbers are not rare. Indeed, almost all real and complex numbers are transcendental, since the algebraic numbers comprise a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic. The converse is not true: not all irrational numbers are transcendental. Hence, the set of real numbers consists of non-overlapping rational, algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of the polynomial . That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number 1 + i is algebraic because it is a root of . All integers and rational numbers are algebraic, as are all roots of integers. Real and complex numbers that are not algebraic, such as and , are called transcendental numbers. The set of algebraic numbers is countably infinite and has measure zero in the Lebesgue measure as a subset of the uncountable complex numbers. In that sense, almost all complex numbers are transcendental. Examples * All rational numbers are algebraic. Any rational number, expressed as the quotient of an integer and a (non-zero) natural number , satisfies the above definition, because is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
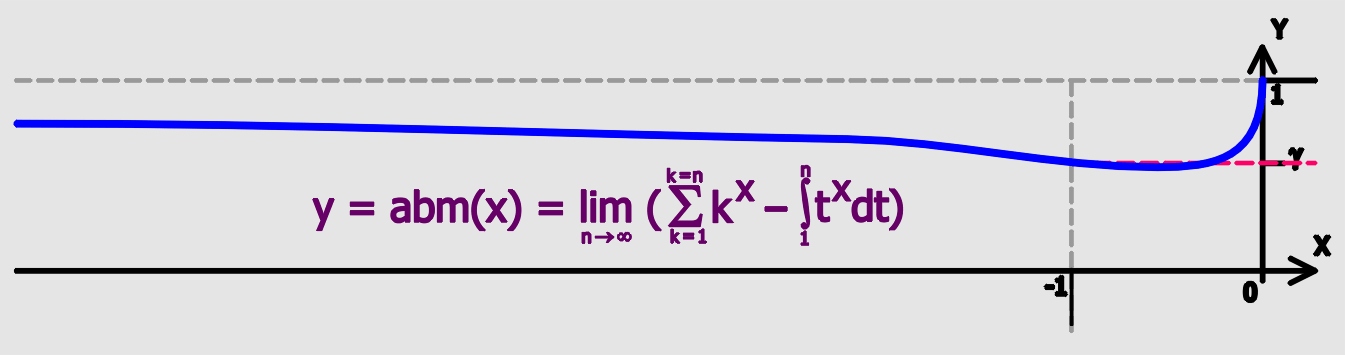Euler–Mascheroni Constant γ
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
