|
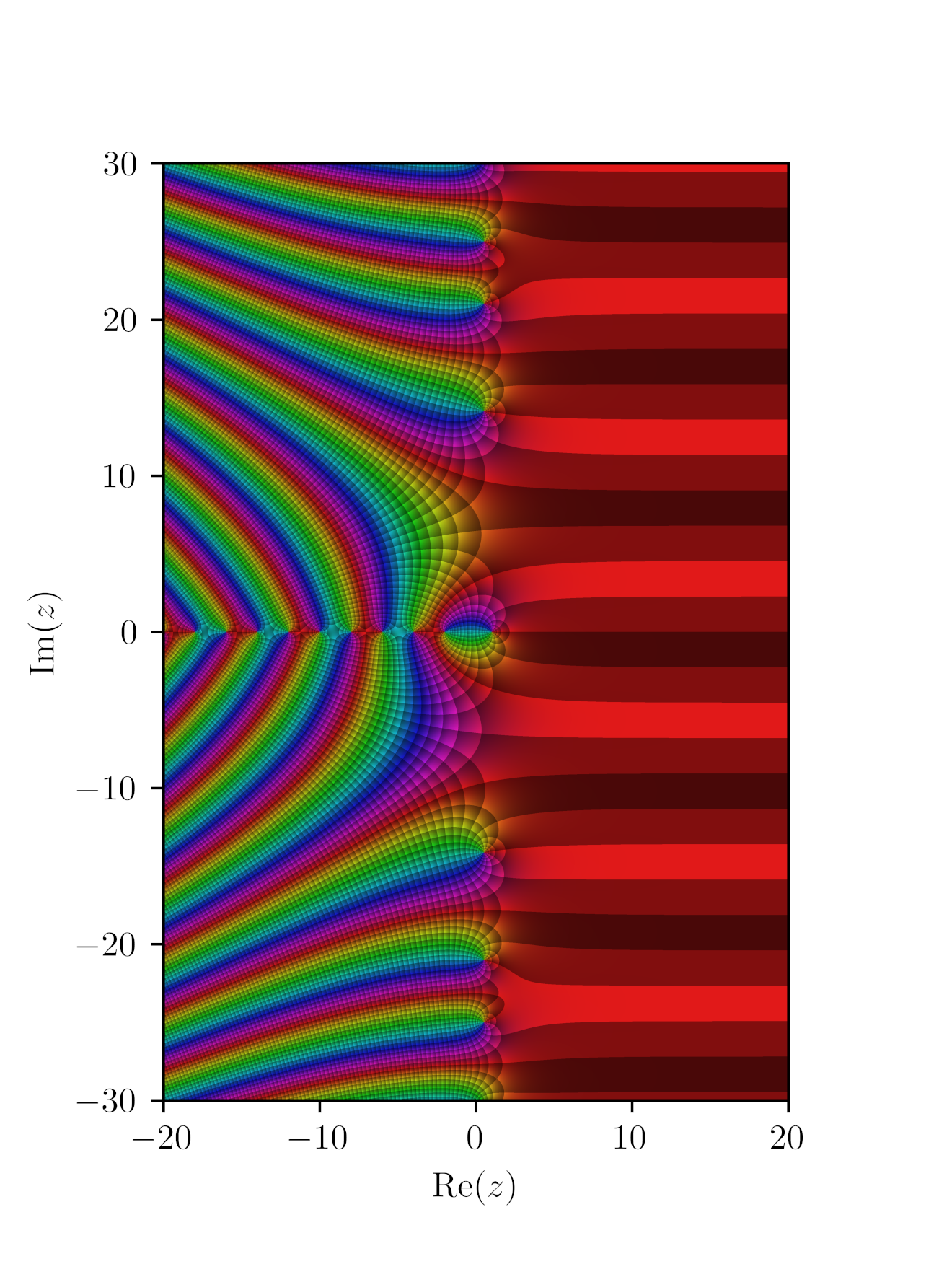
Riemann Zeta-function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is considere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Of A Function
In mathematics, a zero (also sometimes called a root) of a real-, complex-, or generally vector-valued function f, is a member x of the domain of f such that f(x) ''vanishes'' at x; that is, the function f attains the value of 0 at x, or equivalently, x is the solution to the equation f(x) = 0. A "zero" of a function is thus an input value that produces an output of 0. A root of a polynomial is a zero of the corresponding polynomial function. The fundamental theorem of algebra shows that any non-zero polynomial has a number of roots at most equal to its degree, and that the number of roots and the degree are equal when one considers the complex roots (or more generally, the roots in an algebraically closed extension) counted with their multiplicities. For example, the polynomial f of degree two, defined by f(x)=x^2-5x+6 has the two roots (or zeros) that are 2 and 3. f(2)=2^2-5\times 2+6= 0\textf(3)=3^2-5\times 3+6=0. If the function maps real numbers to real numbers, then it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-function
In mathematics, an ''L''-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An ''L''-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an ''L''-function via analytic continuation. The Riemann zeta function is an example of an ''L''-function, and one important conjecture involving ''L''-functions is the Riemann hypothesis and its generalization. The theory of ''L''-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the ''L''-series for a Dirichlet character are constructed, and their general properties, in most cases still out of reach of proof, are set out in a systematic way. Because of the Euler product formula there is a deep connection between ''L''-functions and the theory of prime numbers. The mathematical field that studies L-func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet L-function
In mathematics, a Dirichlet ''L''-series is a function of the form :L(s,\chi) = \sum_^\infty \frac. where \chi is a Dirichlet character and ''s'' a complex variable with real part greater than 1. It is a special case of a Dirichlet series. By analytic continuation, it can be extended to a meromorphic function on the whole complex plane, and is then called a Dirichlet ''L''-function and also denoted ''L''(''s'', ''χ''). These functions are named after Peter Gustav Lejeune Dirichlet who introduced them in to prove the theorem on primes in arithmetic progressions that also bears his name. In the course of the proof, Dirichlet shows that is non-zero at ''s'' = 1. Moreover, if ''χ'' is principal, then the corresponding Dirichlet ''L''-function has a simple pole at ''s'' = 1. Otherwise, the ''L''-function is entire. Euler product Since a Dirichlet character ''χ'' is completely multiplicative, its ''L''-function can also be written as an Euler product in the half-plane of absol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Series
In mathematics, a Dirichlet series is any series of the form \sum_^\infty \frac, where ''s'' is complex, and a_n is a complex sequence. It is a special case of general Dirichlet series. Dirichlet series play a variety of important roles in analytic number theory. The most usually seen definition of the Riemann zeta function is a Dirichlet series, as are the Dirichlet L-functions. It is conjectured that the Selberg class of series obeys the generalized Riemann hypothesis. The series is named in honor of Peter Gustav Lejeune Dirichlet. Combinatorial importance Dirichlet series can be used as generating series for counting weighted sets of objects with respect to a weight which is combined multiplicatively when taking Cartesian products. Suppose that ''A'' is a set with a function ''w'': ''A'' → N assigning a weight to each of the elements of ''A'', and suppose additionally that the Fiber (mathematics), fibre over any natural number under that weight is a finite set. (We call such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Form
In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the Group action (mathematics), group action of the modular group, and also satisfying a growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology, sphere packing, and string theory. A modular function is a function that is invariant with respect to the modular group, but without the condition that be Holomorphic function, holomorphic in the upper half-plane (among other requirements). Instead, modular functions are Meromorphic function, meromorphic (that is, they are holomorphic on the complement of a set of isolated points, which are poles of the function). Modular form theory is a special case of the more general theory of automorphic form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is uncountable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apéry's Constant
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number : \begin \zeta(3) &= \sum_^\infty \frac \\ &= \lim_ \left(\frac + \frac + \cdots + \frac\right), \end where is the Riemann zeta function. It has an approximate value of : . The constant is named after Roger Apéry. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics. It also arises in the analysis of random minimum spanning trees and in conjunction with the gamma function when solving certain integrals involving exponential functions in a quotient, which appear occasionally in physics, for instance, when evaluating the two-dimensional case of the Debye model and the Stefan–Boltzmann law. Irrational number was named ''Apéry's constant'' after the French mathematician Roger Apéry, who proved in 1978 that it is an ir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roger Apéry
Roger Apéry (; 14 November 1916, Rouen – 18 December 1994, Caen) was a French mathematician most remembered for Apéry's theorem, which states that is an irrational number. Here, denotes the Riemann zeta function. Biography Apéry was born in Rouen in 1916 to a French mother and Greek father. His childhood was spent in Lille until 1926, when the family moved to Paris, where he studied at the Lycée Ledru-Rollin and the Lycée Louis-le-Grand. He was admitted at the École normale supérieure in 1935. His studies were interrupted at the start of World War II; he was mobilized in September 1939, taken prisoner of war in June 1940, repatriated with pleurisy in June 1941, and hospitalized until August 1941. He wrote his doctoral thesis in algebraic geometry under the direction of Paul Dubreil and René Garnier in 1947. In 1947 Apéry was appointed Maître de conférences (lecturer) at the University of Rennes. In 1949 he was appointed Professor at the University of Caen, whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basel Problem
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in ''The Saint Petersburg Academy of Sciences''. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up years later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem. The Basel problem asks for the precise summation of the reciprocals of the squares of the natural numbers, i.e. the precise sum of the infinite series: \sum_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clay Mathematics Institute
The Clay Mathematics Institute (CMI) is a private, non-profit foundation (nonprofit), foundation dedicated to increasing and disseminating mathematics, mathematical knowledge. Formerly based in Peterborough, New Hampshire, the corporate address is now in Denver, Colorado. CMI's scientific activities are managed from the President's office in Oxford, United Kingdom. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998 through the sponsorship of Boston businessman Landon T. Clay. Harvard University, Harvard mathematician Arthur Jaffe was the first president of CMI. While the institute is best known for its Millennium Prize Problems, it carries out a wide range of activities, including a postdoctoral program (ten Clay Research Fellows are supported currently), conferences, workshops, and summer schools. Governance The institute is run according to a standard structure comprising a scientific advisory committee that decides on gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications, but pure mathematicians are not primarily motivated by such applications. Instead, the appeal is attributed to the intellectual challenge and aesthetic beauty of working out the logical consequences of basic principles. While pure mathematics has existed as an activity since at least Ancient Greece, the concept was elaborated upon around the year 1900, after the introduction of theories with counter-intuitive properties (such as non-Euclidean geometries and Cantor's theory of infinite sets), and the discovery of apparent paradoxes (such as continuous functions that are nowhere differentiable, and Russell's paradox). This introduced the need to renew the concept of mathematical rigor and rewrite all mathematics accordingly, with a system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |