|
Richard Von Mises
Richard Edler von Mises (; 19 April 1883 – 14 July 1953) was an Austrian scientist and mathematician who worked on solid mechanics, fluid mechanics, aerodynamics, aeronautics, statistics and probability theory. He held the position of Gordon McKay Professor of Aerodynamics and Applied Mathematics at Harvard University. He described his work in his own words shortly before his death as being on :"... practical analysis, integral and differential equations, mechanics, hydrodynamics and aerodynamics, constructive geometry, probability calculus, statistics and philosophy." Although best known for his mathematical work, von Mises also contributed to the philosophy of science as a neo-positivist and empiricist, following the line of Ernst Mach. Historians of the Vienna Circle of logical empiricism recognize a "first phase" from 1907 through 1914 with Philipp Frank, Hans Hahn, and Otto Neurath. His older brother, Ludwig von Mises, held an opposite point of view with respect to po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludwig Von Mises
Ludwig Heinrich Edler von Mises (; 29 September 1881 – 10 October 1973) was an Austrian School economist, historian, logician, and Sociology, sociologist. Mises wrote and lectured extensively on the societal contributions of classical liberalism. He is best known for his work on praxeology studies Bureaucracy (book), comparing communism and capitalism. He is considered one of the most influential economic and political thinkers of the 20th century. Mises emigrated from Austria to the United States in 1940. Since the mid-20th century, libertarian movements have been strongly influenced by Mises's writings. Mises' student Friedrich Hayek viewed Mises as one of the major figures in the revival of classical liberalism in the post-war era. Hayek's work "The Transmission of the Ideals of Freedom" (1951) pays high tribute to the influence of Mises in the 20th century libertarian movement. Mises's Private Seminar was a leading group of economists. Many of its alumni, including Friedri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Istanbul
, image = Istanbul_University_logo.svg , image_size = 200px , latin_name = Universitas Istanbulensis , motto = tr, Tarihten Geleceğe Bilim Köprüsü , mottoeng = Science Bridge from Past to the Future , established = 1453 1846 1933 , type = Public university Research university , rector = Prof. Dr. Mahmut Ak , students = 69,411 , undergrad = 51,714 , postgrad = 16,669 , academic_staff = 4,101 , city = Istanbul , country = Turkey , campus = Beyazıt CampusVezneciler CampusAvcılar CampusÇapa CampusKadıköy Campus , coor = , colors = Green Yellow , affiliations = Coimbra Group EUA UNIMED , website = , free_label = Founder , free = Mehmed II Istanbul University ( tr, İstanbul Üniversitesi) is a prominent public research university located in Istanbul, Turkey. Founded by Mehmed II on May 30, 1453, a day after the conquest of Constantinople by the Turks, it was reformed in 1846 as the first Ottoman higher education institution based on Europea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
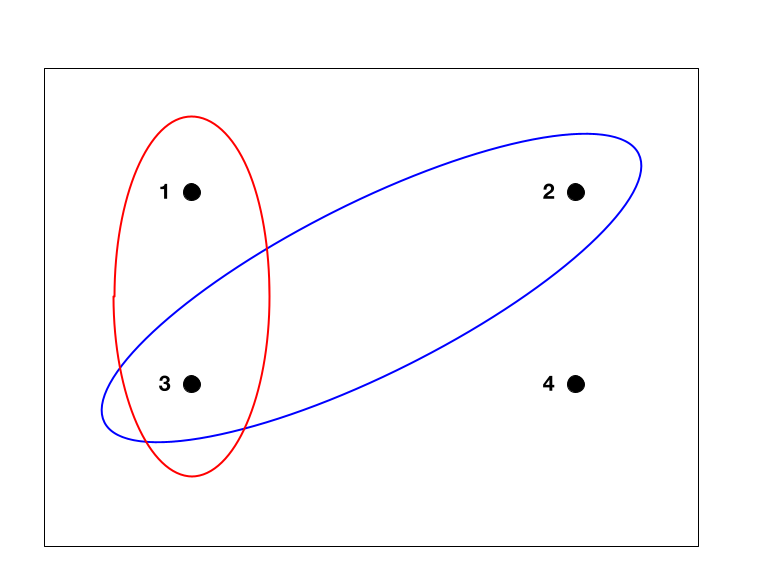
Sample Space
In probability theory, the sample space (also called sample description space, possibility space, or outcome space) of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes, or sample points, are listed as elements in the set. It is common to refer to a sample space by the labels ''S'', Ω, or ''U'' (for "universal set"). The elements of a sample space may be numbers, words, letters, or symbols. They can also be finite, countably infinite, or uncountably infinite. A subset of the sample space is an event, denoted by E. If the outcome of an experiment is included in E, then event E has occurred. For example, if the experiment is tossing a single coin, the sample space is the set \, where the outcome H means that the coin is heads and the outcome T means that the coin is tails. The possible events are E=\, E = \, and E = \. For tossing two coins, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let ''X''1,...,''Xn'' be independent random variables...". Yet as D. H. Lehmer stated in 1951: "A random sequence is a vague notion... in which each term is unpredictable to the uninitiated and whose digits pass a certain number of tests traditional with statisticians". Axiomatic probability theory ''deliberately'' avoids a definition of a random sequence. Traditional probability theory does not state if a specific sequence is random, but generally proceeds to discuss the properties of random variables and stochastic sequences assuming some definition of randomness. The Bourbaki school considered the statement "let us consider a random sequence" an abuse of language. Early history Émile Borel was one of the first mathematicians to formally address randomness in 190 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises–Fisher Distribution
In directional statistics, the von Mises–Fisher distribution (named after Richard von Mises and Ronald Fisher), is a probability distribution on the (p-1)-sphere in \mathbb^. If p=2 the distribution reduces to the von Mises distribution on the circle. Definition The probability density function of the von Mises–Fisher distribution for the random ''p''-dimensional unit vector \mathbf is given by: :f_(\mathbf; \boldsymbol, \kappa) = C_(\kappa) \exp \left( \right), where \kappa \ge 0, \left \Vert \boldsymbol \right \Vert = 1 and the normalization constant C_(\kappa) is equal to : C_(\kappa)=\frac , where I_ denotes the modified Bessel function of the first kind at order v. If p = 3, the normalization constant reduces to : C_(\kappa) = \frac = \frac . The parameters \boldsymbol and \kappa are called the ''mean direction'' and ''concentration parameter'', respectively. The greater the value of \kappa, the higher the concentration of the distribution around the mean di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Yield Criterion
The maximum distortion criterion (also von Mises yield criterion) states that yielding of a ductile material begins when the second invariant of deviatoric stress J_2 reaches a critical value. It is a part of plasticity theory that mostly applies to ductile materials, such as some metals. Prior to yield, material response can be assumed to be of a nonlinear elastic, viscoelastic, or linear elastic behavior. In materials science and engineering von Mises yield criterion is also formulated in terms of the von Mises stress or equivalent tensile stress, \sigma_\text. This is a scalar value of stress that can be computed from the Cauchy stress tensor. In this case, a material is said to start yielding when the von Mises stress reaches a value known as yield strength, \sigma_\text. The von Mises stress is used to predict yielding of materials under complex loading from the results of uniaxial tensile tests. The von Mises stress satisfies the property where two stress states with equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramér–von Mises Criterion
In statistics the Cramér–von Mises criterion is a criterion used for judging the goodness of fit of a cumulative distribution function F^* compared to a given empirical distribution function F_n, or for comparing two empirical distributions. It is also used as a part of other algorithms, such as minimum distance estimation. It is defined as :\omega^2 = \int_^ _n(x) - F^*(x)2\,\mathrmF^*(x) In one-sample applications F^* is the theoretical distribution and F_n is the empirically observed distribution. Alternatively the two distributions can both be empirically estimated ones; this is called the two-sample case. The criterion is named after Harald Cramér and Richard Edler von Mises who first proposed it in 1928–1930. The generalization to two samples is due to Anderson. The Cramér–von Mises test is an alternative to the Kolmogorov–Smirnov test (1933). Cramér–von Mises test (one sample) Let x_1,x_2,\cdots,x_n be the observed values, in increasing order. Then th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernstein–von Mises Theorem
In Bayesian inference, the Bernstein-von Mises theorem provides the basis for using Bayesian credible sets for confidence statements in parametric models. It states that under some conditions, a posterior distribution converges in the limit of infinite data to a multivariate normal distribution centered at the maximum likelihood estimator with covariance matrix given by n^ I(\theta_0)^ , where \theta_0 is the true population parameter and I(\theta_0) is the Fisher information matrix at the true population parameter value. The Bernstein-von Mises theorem links Bayesian inference with frequentist inference. It assumes there is some true probabilistic process that generates the observations, as in frequentism, and then studies the quality of Bayesian methods of recovering that process, and making uncertainty statements about that process. In particular, it states that Bayesian credible sets of a certain credibility level \alpha will asymptotically be confidence sets of confidence le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Statistic
V-statistics are a class of statistics named for Richard von Mises who developed their asymptotic distribution theory in a fundamental paper in 1947. V-statistics are closely related to U-statistics (U for "unbiased") introduced by Wassily Hoeffding in 1948. A V-statistic is a statistical function (of a sample) defined by a particular statistical functional of a probability distribution. Statistical functions Statistics that can be represented as functionals T(F_n) of the empirical distribution function (F_n) are called ''statistical functionals''. Differentiability of the functional ''T'' plays a key role in the von Mises approach; thus von Mises considers ''differentiable statistical functionals''. Examples of statistical functions The ''k''-th central moment is the ''functional'' T(F)=\int(x-\mu)^k \, dF(x), where \mu = E /math> is the expected value of ''X''. The associated ''statistical function'' is the sample ''k''-th central moment, : T_n=m_k=T(F_n) = \frac 1n \su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Layer
In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition (zero velocity at the wall). The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer. The air next to a human is heated resulting in gravity-induced convective airflow, airflow which results in both a velocity and thermal boundary layer. A breeze disrupts the boundary layer, and hair and clothing protect it, making the human feel cooler or warmer. On an aircraft wing, the velocity boundary layer is the part of the flow close to the wing, where viscous forces distort the surrounding non-viscous flow. In the Earth's atmosphere, the atmospheric boun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Distribution
In probability theory and directional statistics, the von Mises distribution (also known as the circular normal distribution or Tikhonov distribution) is a continuous probability distribution on the circle. It is a close approximation to the wrapped normal distribution, which is the circular analogue of the normal distribution. A freely diffusing angle \theta on a circle is a wrapped normally distributed random variable with an unwrapped variance that grows linearly in time. On the other hand, the von Mises distribution is the stationary distribution of a drift and diffusion process on the circle in a harmonic potential, i.e. with a preferred orientation. The von Mises distribution is the maximum entropy distribution for circular data when the real and imaginary parts of the first circular moment are specified. The von Mises distribution is a special case of the von Mises–Fisher distribution on the ''N''-dimensional sphere. Definition The von Mises probability density funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermine Agavni Kalustyan
Hermine Agavni Kalustyan ( hy, Հերմինէ Աղաւնի Գալուստեան, 1914 – September 3, 1989) was an Armenian–Turkish mathematician, educator, and politician. Kalustyan was born in 1914 in Istanbul. She graduated from Paris High School Teacher Training School and from Istanbul University Mathematics Department. In 1941, she wrote her dissertation titled "Conformal depiction and the movement of an object" in the Istanbul University under Richard von Mises and William Prager William Prager, (before 1940) Willy Prager, (May 23, 1903 in Karlsruhe – March 17, 1980 in Zurich) was a German-born US applied mathematician. In the field of mechanics he is well known for the Drucker–Prager yield criterion. Willy Prager st .... Between 1948 and 1973, Kalustyan was appointed principal at Esayan Armenian High School, and taught mathematics at the Galatasaray High School in Istanbul, Turkey. In 1961, she became the republic's first non-Muslim minority woman to serve in par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
