|
Restricted Isometry Property
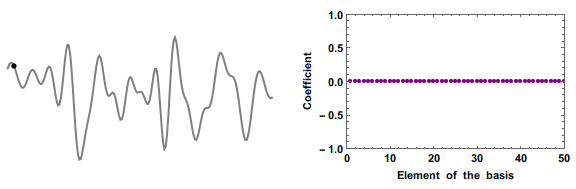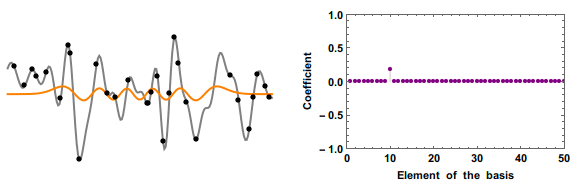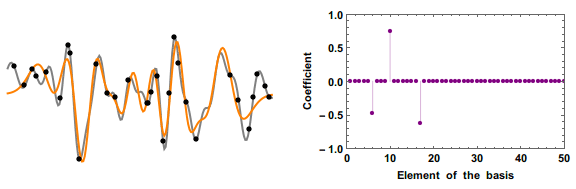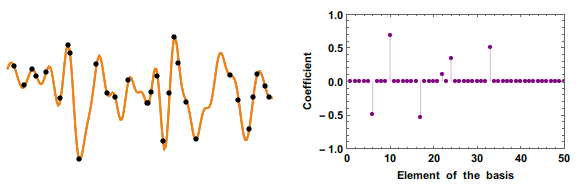
In linear algebra, the restricted isometry property (RIP) characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence TaoE. J. Candes and T. Tao, "Decoding by Linear Programming," IEEE Trans. Inf. Th., 51(12): 4203–4215 (2005). and is used to prove many theorems in the field of compressed sensing. There are no known large matrices with bounded restricted isometry constants (computing these constants is strongly NP-hard, and is hard to approximate as well), but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level. The current smallest upper bounds for any large rectangular matrices are for those of Gaussian matrices. Web forms to evaluate bounds for the Gaussian ensemble ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the linear ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Emmanuel Candès
Emmanuel Jean Candès (born 27 April 1970) is a French statistician. He is a professor of statistics and electrical engineering (by courtesy) at Stanford University, where he is also the Barnum-Simons Chair in Mathematics and Statistics. Candès is a 2017 MacArthur Fellow. Academic biography Candès earned a MSc from the École Polytechnique in 1993.Speaker bio from NIPS 2008. He did his postgraduate studies at , where he earned a PhD in statistics in 1998 under the supervision of |
Terence Tao
Terence Chi-Shen Tao (; born 17 July 1975) is an Australian-American mathematician. He is a professor of mathematics at the University of California, Los Angeles (UCLA), where he holds the James and Carol Collins chair. His research includes topics in harmonic analysis, partial differential equations, algebraic combinatorics, arithmetic combinatorics, geometric combinatorics, probability theory, compressed sensing and analytic number theory. Tao was born to ethnic Chinese immigrant parents and raised in Adelaide. Tao won the Fields Medal in 2006 and won the Royal Medal and Breakthrough Prize in Mathematics in 2014. He is also a 2006 MacArthur Fellow. Tao has been the author or co-author of over three hundred research papers. He is widely regarded as one of the greatest living mathematicians and has been referred to as the "Mozart of mathematics". Life and career Family Tao's parents are first-generation immigrants from Hong Kong to Australia.''Wen Wei Po'', Page A4, 24 Au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series of sampling measurements. In general, this task is impossible because there is no way to reconstruct a signal during the times that the signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strongly NP-hard
In computational complexity, strong NP-completeness is a property of computational problems that is a special case of NP-completeness. A general computational problem may have numerical parameters. For example, the input to the bin packing problem is a list of objects of specific sizes and a size for the bins that must contain the objects—these object sizes and bin size are numerical parameters. A problem is said to be strongly NP-complete (NP-complete in the strong sense), if it remains NP-complete even when all of its numerical parameters are bounded by a polynomial in the length of the input. A problem is said to be strongly NP-hard if a strongly NP-complete problem has a polynomial reduction to it; in combinatorial optimization, particularly, the phrase "strongly NP-hard" is reserved for problems that are not known to have a polynomial reduction to another strongly NP-complete problem. Normally numerical parameters to a problem are given in positional notation, so a prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator Norm
In mathematics, the operator norm measures the "size" of certain linear operators by assigning each a real number called its . Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces. Introduction and definition Given two normed vector spaces V and W (over the same base field, either the real numbers \R or the complex numbers \Complex), a linear map A : V \to W is continuous if and only if there exists a real number c such that \, Av\, \leq c \, v\, \quad \mbox v\in V. The norm on the left is the one in W and the norm on the right is the one in V. Intuitively, the continuous operator A never increases the length of any vector by more than a factor of c. Thus the image of a bounded set under a continuous operator is also bounded. Because of this property, the continuous linear operators are also known as bounded operators. In order to "measure the size" of A, one can take the infimum of the numbers c such that the above i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infimum And Supremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lower bound'' (abbreviated as ) is also commonly used. The supremum (abbreviated sup; plural suprema) of a subset S of a partially ordered set P is the least element in P that is greater than or equal to each element of S, if such an element exists. Consequently, the supremum is also referred to as the ''least upper bound'' (or ). The infimum is in a precise sense dual to the concept of a supremum. Infima and suprema of real numbers are common special cases that are important in analysis, and especially in Lebesgue integration. However, the general definitions remain valid in the more abstract setting of order theory where arbitrary partially ordered sets are considered. The concepts of infimum and supremum are close to minimum and maxim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series of sampling measurements. In general, this task is impossible because there is no way to reconstruct a signal during the times that the signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Coherence (linear Algebra)
In linear algebra, the coherence or mutual coherence of a matrix ''A'' is defined as the maximum absolute value of the cross-correlations between the columns of ''A''. Formally, let a_1, \ldots, a_m\in ^d be the columns of the matrix ''A'', which are assumed to be normalized such that a_i^H a_i = 1. The mutual coherence of ''A'' is then defined as :M = \max_ \left, a_i^H a_j \. A lower bound is : M\ge \sqrt A deterministic matrix with the mutual coherence almost meeting the lower bound can be constructed by Weil's theorem. This concept was reintroduced by David Donoho and Michael Elad in the context of sparse representations. A special case of this definition for the two-ortho case appeared earlier in the paper by Donoho and Huo. The mutual coherence has since been used extensively in the field of sparse representations of signals. In particular, it is used as a measure of the ability of suboptimal algorithms such as matching pursuit and basis pursuit to correctly identif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nullspace Property
In compressed sensing, the Kernel (linear algebra), nullspace property gives necessary and sufficient conditions on the reconstruction of sparse signals using the techniques of Relaxation (approximation), \ell_1-relaxation. The term "nullspace property" originates from Cohen, Dahmen, and DeVore. The nullspace property is often difficult to check in practice, and the restricted isometry property is a more modern condition in the field of compressed sensing. The technique of Relaxation (approximation), \ell_1-relaxation The Convex optimization, non-convex \ell_0-minimization problem, \min\limits_ \, x\, _0 subject to Ax = b, is a standard problem in compressed sensing. However, \ell_0-minimization is known to be NP-hardness, NP-hard in general. As such, the technique of Relaxation (approximation), \ell_1-relaxation is sometimes employed to circumvent the difficulties of signal reconstruction using the \ell_0-norm. In Relaxation (approximation), \ell_1-relaxation, the Relaxation (a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
