|
Resistivity Probes
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter (rho). The SI unit of electrical resistivity is the ohm-meter (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is , then the resistivity of the material is . Electrical conductivity or specific conductance is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter (sigma), but (kappa) (especially in electrical engineering) and (gamma) are sometimes used. The SI unit of electrical conductivity is siemens per metre (S/m). Resistivity and conductivity are intensiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Current
An electric current is a stream of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is measured as the net rate of flow of electric charge through a surface or into a control volume. The moving particles are called charge carriers, which may be one of several types of particles, depending on the conductor. In electric circuits the charge carriers are often electrons moving through a wire. In semiconductors they can be electrons or holes. In an electrolyte the charge carriers are ions, while in plasma, an ionized gas, they are ions and electrons. The SI unit of electric current is the ampere, or ''amp'', which is the flow of electric charge across a surface at the rate of one coulomb per second. The ampere (symbol: A) is an SI base unit. Electric current is measured using a device called an ammeter. Electric currents create magnetic fields, which are used in motors, generators, inductors, and transformers. In ordinary con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Section (geometry)
In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation. In technical drawing a cross-section, being a projection of an object onto a plane that intersects it, is a common tool used to depict the internal arrangement of a 3-dimensional object in two dimensions. It is traditionally crosshatched with the style of crosshatching often indicating the types of materials being used. With computed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Notation
In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916. Introduction Statement of convention According to this convention, when an index variable appears twice in a single term and is not otherwise defined (see Free and bound variables), it implies summation of that term over all the values of the index. So where the indices can range over the set , : y = \sum_^3 c_i x^i = c_1 x^1 + c_2 x^2 + c_3 x^3 is simplified by the convention to: : y = c_i x^i The upper indices are not exponents but are indices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Multiplication
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices and is denoted as . Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. Notation This article will use the following notati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity ( stress–energy tensor, cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
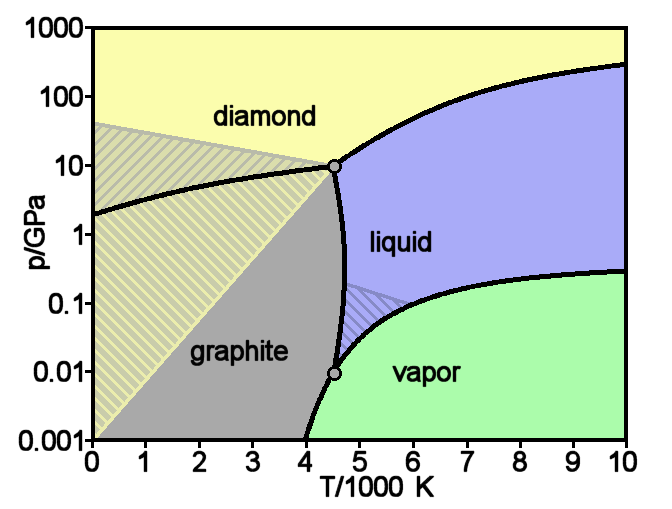
Graphite
Graphite () is a crystalline form of the element carbon. It consists of stacked layers of graphene. Graphite occurs naturally and is the most stable form of carbon under standard conditions. Synthetic and natural graphite are consumed on large scale (300 kton/year, in 1989) for uses in pencils, lubricants, and electrodes. Under high pressures and temperatures it converts to diamond. It is a weak conductor of heat and electricity. Types and varieties Natural graphite The principal types of natural graphite, each occurring in different types of ore deposits, are * Crystalline small flakes of graphite (or flake graphite) occurs as isolated, flat, plate-like particles with hexagonal edges if unbroken. When broken the edges can be irregular or angular; * Amorphous graphite: very fine flake graphite is sometimes called amorphous; * Lump graphite (or vein graphite) occurs in fissure veins or fractures and appears as massive platy intergrowths of fibrous or acicular crystalline ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anisotropy
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties (absorbance, refractive index, conductivity, tensile strength, etc.). An example of anisotropy is light coming through a polarizer. Another is wood, which is easier to split along its grain than across it. Fields of interest Computer graphics In the field of computer graphics, an anisotropic surface changes in appearance as it rotates about its geometric normal, as is the case with velvet. Anisotropic filtering (AF) is a method of enhancing the image quality of textures on surfaces that are far away and steeply angled with respect to the point of view. Older techniques, such as bilinear and trilinear filtering, do not take into account the angle a surface is viewed from, which can result in aliasing or bl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anisotropy
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties (absorbance, refractive index, conductivity, tensile strength, etc.). An example of anisotropy is light coming through a polarizer. Another is wood, which is easier to split along its grain than across it. Fields of interest Computer graphics In the field of computer graphics, an anisotropic surface changes in appearance as it rotates about its geometric normal, as is the case with velvet. Anisotropic filtering (AF) is a method of enhancing the image quality of textures on surfaces that are far away and steeply angled with respect to the point of view. Older techniques, such as bilinear and trilinear filtering, do not take into account the angle a surface is viewed from, which can result in aliasing or bl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ohm's Law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this relationship: :I = \frac, where is the current through the conductor, ''V'' is the voltage measured ''across'' the conductor and ''R'' is the resistance of the conductor. More specifically, Ohm's law states that the ''R'' in this relation is constant, independent of the current. If the resistance is not constant, the previous equation cannot be called ''Ohm's law'', but it can still be used as a definition of static/DC resistance. Ohm's law is an empirical relation which accurately describes the conductivity of the vast majority of electrically conductive materials over many orders of magnitude of current. However some materials do not obey Ohm's law; these are called non-ohmic. The law was named after t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an order theory, ordering (or ranking)—of the class (mathematics), class of objects to which it belongs. In physics, magnitude can be defined as quantity or distance. History The Greeks distinguished between several types of magnitude, including: *Positive fractions *Line segments (ordered by length) *Geometric shape, Plane figures (ordered by area) *Solid geometry, Solids (ordered by volume) *Angle, Angles (ordered by angular magnitude) They proved that the first two could not be the same, or even isomorphic systems of magnitude. They did not consider negative number, negative magnitudes to be meaningful, and ''magnitude'' is still primarily used in contexts in which zero is either the smallest size or less than all possible sizes. Numbers Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Current Density
In electromagnetism, current density is the amount of charge per unit time that flows through a unit area of a chosen cross section. The current density vector is defined as a vector whose magnitude is the electric current per cross-sectional area at a given point in space, its direction being that of the motion of the positive charges at this point. In SI base units, the electric current density is measured in amperes per square metre. Definition Assume that ''A'' (SI unit: m2) is a small surface centred at a given point ''M'' and orthogonal to the motion of the charges at ''M''. If ''I'' (SI unit: A) is the electric current flowing through ''A'', then electric current density ''j'' at ''M'' is given by the limit: :j = \lim_ \frac = \left.\frac \_, with surface ''A'' remaining centered at ''M'' and orthogonal to the motion of the charges during the limit process. The current density vector j is the vector whose magnitude is the electric current density, and whose dire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes E-field) is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions (also called forces) of nature. Electric fields are important in many areas of physics, and are exploited in electrical technology. In atomic physics and chemistry, for instance, the electric field is the attractive force holding the atomic nucleus and electrons together in atoms. It is also the force responsible for chemical bonding between atoms that result in molecules. The electric field is defined as a vector field that associates to each point in space the electrostatic ( Coulomb) for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
