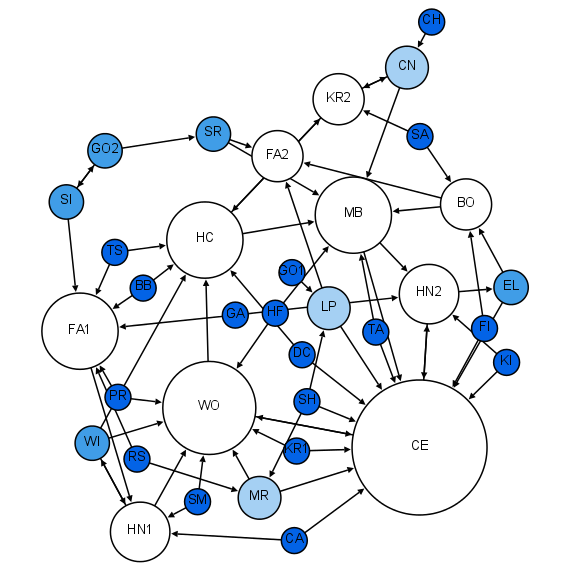
|
Resilience (mathematics)
In mathematical modeling, resilience refers to the ability of a dynamical system to recover from perturbations and return to its original stable steady state. It is a measure of the stability and robustness of a system in the face of changes or disturbances. If a system is not resilient enough, it is more susceptible to perturbations and can more easily undergo a critical transition. A common analogy used to explain the concept of resilience of an equilibrium is one of a ball in a valley. A resilient steady state corresponds to a ball in a deep valley, so any push or perturbation will very quickly lead the ball to return to the resting point where it started. On the other hand, a less resilient steady state corresponds to a ball in a shallow valley, so the ball will take a much longer time to return to the equilibrium after a perturbation. The concept of resilience is particularly useful in systems that exhibit tipping points, whose study has a long history that can be traced bac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resilience Diagram
Resilience, resilient, or resiliency may refer to: Science Ecology * Ecological resilience, the capacity of an ecosystem to recover from perturbations ** Climate resilience, the ability of systems to recover from climate change ** Soil resilience, the ability of a soil to maintain a healthy state in response to destabilising influences Social sciences * Resilience in art, the property of artwork to remain relevant over changing times * Resilience (organizational), the ability of a system to withstand changes in its environment and still function * Psychological resilience, an individual's ability to adapt in the face of adverse conditions * Supply chain resilience, the capacity of a supply chain to persist, adapt, or transform in the face of change * Urban resilience, the adaptive capacities of complex urban systems to manage change, order and disorder over time * Community resilience, the adaptive capacities of communities and societies to manage change and adversities over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Transition
Critical transitions are abrupt shifts in the state of ecosystems, the climate, financial and economic systems or other complex system, complex dynamical systems that may occur when changing conditions pass a critical or bifurcation theory, bifurcation point. As such, they are a particular type of regime shift. Recovery from such shifts may require more than a simple return to the conditions at which a transition occurred, a phenomenon called hysteresis. In addition to natural systems, critical transitions are also studied in psychology, medicine, economics, sociology, military, and several other disciplines. Early-warning signals Critical slow down Significant efforts have been made to identify early-warning signals of critical transitions.Scheffer, M., et al. (2009) Early-warning signals for critical transitions. ''Nature'' 461, 53–59Dakos, V., et al. (2008) Slowing down as an early warning signal for abrupt climate change. ''P Natl Acad Sci Usa'' 105, 14308–14312van Nes, E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Terminology
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Modeling
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Theory
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematics, mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by Ordinary differential equation, ordinary, Delay differential equation, delay or Partial differential equation, partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecological Resilience
In ecology, resilience is the capacity of an ecosystem to respond to a perturbation or Disturbance (ecology), disturbance by resisting damage and subsequently recovering. Such perturbations and disturbances can include stochastic events such as fires, flooding, windstorms, insect population explosions, and human activities such as deforestation, fracking of the ground for oil extraction, pesticide sprayed in soil, and the Introduced species, introduction of exotic plant or animal species. Disturbances of sufficient Magnitude (mathematics), magnitude or duration can profoundly affect an ecosystem and may force an ecosystem to reach a Ecological threshold, threshold beyond which a different regime of processes and structures predominates. When such thresholds are associated with a critical or bifurcation theory, bifurcation point, these regime shifts may also be referred to as critical transitions. Human activities that adversely affect ecological resilience such as loss of biodiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resilience (engineering And Construction)
In the fields of engineering and construction, resilience is the ability to absorb or avoid damage without suffering complete failure and is an objective of design, maintenance and restoration for buildings and infrastructure, as well as communities. A more comprehensive definition is that it is the ability to respond, absorb, and adapt to, as well as recover in a disruptive event. A resilient structure/system/community is expected to be able to resist to an extreme event with minimal damages and functionality disruptions during the event; after the event, it should be able to rapidly recovery its functionality similar to or even better than the pre-event level. The concept of resilience originated from engineering and then gradually applied to other fields. It is related to that of vulnerability. Both terms are specific to the event perturbation, meaning that a system/infrastructure/community may be more vulnerable or less resilient to one event than another one. However, they a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale-free Network
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction ''P''(''k'') of nodes in the network having ''k'' connections to other nodes goes for large values of ''k'' as : P(k) \ \sim \ k^\boldsymbol where \gamma is a parameter whose value is typically in the range 2<\gamma<3 (wherein the second moment ( scale parameter) of is infinite but the first moment is finite), although occasionally it may lie outside these bounds. The name "scale-free" could be explained by the fact that some moments of the degree distribution are not defined, so that the network does not have a characteristic scale or "size". and the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, Cognitive network, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential statistics, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex System
A complex system is a system composed of many components that may interact with one another. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, complex software and electronic systems, social and economic organizations (like cities), an ecosystem, a living Cell (biology), cell, and, ultimately, for some authors, the entire universe. The behavior of a complex system is intrinsically difficult to model due to the dependencies, competitions, relationships, and other types of interactions between their parts or between a given system and its environment. Systems that are "Complexity, complex" have distinct properties that arise from these relationships, such as Nonlinear system, nonlinearity, emergence, spontaneous order, Complex adaptive system, adaptation, and Feedback, feedback loops, among others. Because such systems appear in a wide variety of fields, the commonalities am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |