|
Relativistic Breit–Wigner Distribution
The relativistic Breit–Wigner distribution (after the 1936 nuclear resonance formula of Gregory Breit and Eugene Wigner) is a continuous probability distribution with the following probability density function, SePythia 6.4 Physics and Manual(page 98 onwards) for a discussion of the widths of particles in the PYTHIA manual. Note that this distribution is usually represented as a function of the squared energy. : f(E) = \frac~, where is a constant of proportionality, equal to : k = \frac ~~~~ with ~~~~ \gamma=\sqrt ~. (This equation is written using natural units, .) It is most often used to model resonances (unstable particles) in high-energy physics. In this case, is the center-of-mass energy that produces the resonance, is the mass of the resonance, and Γ is the resonance width (or '' decay width''), related to its mean lifetime according to . (With units included, the formula is .) Usage The probability of producing the resonance at a given energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gregory Breit
Gregory Breit (russian: Григорий Альфредович Брейт-Шнайдер, ''Grigory Alfredovich Breit-Shneider''; July 14, 1899, Mykolaiv, Kherson Governorate – September 13, 1981, Salem, Oregon) was a Russian-born Jewish American physicist and professor at New York University (1929–1934), University of Wisconsin–Madison (1934–1947), Yale University (1947–1968), and University at Buffalo (1968–1973). In 1921, he was Paul Ehrenfest's assistant in Leiden University. Biography After completing his Ph.D. at age 22, he was from 1923 to 1924 an assistant professor at the University of Minnesota. In 1925, while at the Carnegie Institution of Washington, Breit joined with Merle Tuve in using a pulsed radio transmitter to determine the height of the ionosphere, a technique important later in radar development. Together with Eugene Wigner, Breit gave a description of particle resonant states with the relativistic Breit–Wigner distribution in 1929, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Rho Meson
Rho (uppercase Ρ, lowercase ρ or ; el, ρο or el, ρω, label=none) is the 17th letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the same glyph, Ρ, as the distinct Latin letter P; the two letters have different Unicode encodings. Uses Greek Rho is classed as a liquid consonant (together with Lambda and sometimes the nasals Mu and Nu), which has important implications for morphology. In both Ancient and Modern Greek, it represents a alveolar trill , alveolar tap , or alveolar approximant . In polytonic orthography, a rho at the beginning of a word is written with a rough breathing, equivalent to ''h'' ( ''rh''), and a double rho within a word is written with a smooth breathing over the first rho and a rough breathing over the second ( ''rrh''). That apparently reflected an aspirated or voiceless pronunciation in Ancient Greek, which led to the various Greek- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Voigt Profile
The Voigt profile (named after Woldemar Voigt) is a probability distribution given by a convolution of a Cauchy-Lorentz distribution and a Gaussian distribution. It is often used in analyzing data from spectroscopy or diffraction. Definition Without loss of generality, we can consider only centered profiles, which peak at zero. The Voigt profile is then : V(x;\sigma,\gamma) \equiv \int_^\infty G(x';\sigma)L(x-x';\gamma)\, dx', where ''x'' is the shift from the line center, G(x;\sigma) is the centered Gaussian profile: : G(x;\sigma) \equiv \frac, and L(x;\gamma) is the centered Lorentzian profile: : L(x;\gamma) \equiv \frac. The defining integral can be evaluated as: : V(x;\sigma,\gamma)=\frac, where Re 'w''(''z'')is the real part of the Faddeeva function evaluated for : z=\frac. In the limiting cases of \sigma=0 and \gamma =0 then V(x;\sigma,\gamma) simplifies to L(x;\gamma) and G(x;\sigma), respectively. History and applications In spectroscopy, a Vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Cauchy Distribution
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f(x; x_0,\gamma) is the distribution of the -intercept of a ray issuing from (x_0,\gamma) with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero. The Cauchy distribution is often used in statistics as the canonical example of a " pathological" distribution since both its expected value and its variance are undefined (but see below). The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist., Chapter 16. The Cauchy distribution has no moment generating function. In mathematics, it is closely related to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
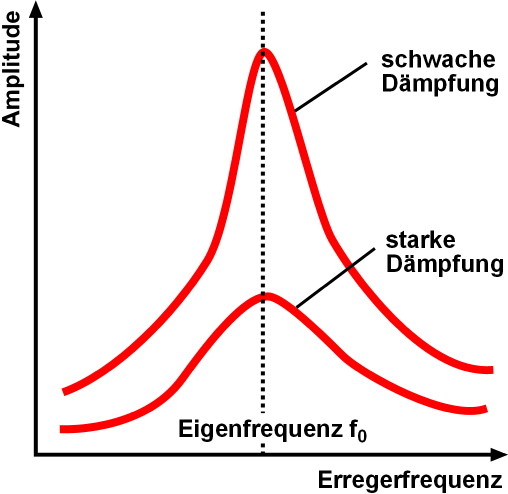 |
Resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Sinusoidal
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', '' ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', '' angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive coefficient, constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (Damping ratio, damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the Damping ratio, undamped case, and an amplitude decreasing with time (Damping ratio, underdamped oscillator). * Decay to the equilibrium p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Probability Amplitude
In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The modulus squared of this quantity represents a probability density. Probability amplitudes provide a relationship between the quantum state vector of a system and the results of observations of that system, a link was first proposed by Max Born, in 1926. Interpretation of values of a wave function as the probability amplitude is a pillar of the Copenhagen interpretation of quantum mechanics. In fact, the properties of the space of wave functions were being used to make physical predictions (such as emissions from atoms being at certain discrete energies) before any physical interpretation of a particular function was offered. Born was awarded half of the 1954 Nobel Prize in Physics for this understanding, and the probability thus calculated is sometimes called the "Born probability". These probabilistic concepts, namely the probability density and quantum measurem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Four-momentum
In special relativity, four-momentum (also called momentum-energy or momenergy ) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy and three-momentum , where is the particle's three-velocity and the Lorentz factor, is p = \left(p^0 , p^1 , p^2 , p^3\right) = \left(\frac E c , p_x , p_y , p_z\right). The quantity of above is ordinary non-relativistic momentum of the particle and its rest mass. The four-momentum is useful in relativistic calculations because it is a Lorentz covariant vector. This means that it is easy to keep track of how it transforms under Lorentz transformations. The above definition applies under the coordinate convention that . Some authors use the convention , which yields a modified definition with . It is also possible to define covar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Propagator
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called ''(causal) Green's functions'' (called "''causal''" to distinguish it from the elliptic Laplacian Green's function). Non-relativistic propagators In non-relativistic quantum mechanics, the propagator gives the probability amplitude for a particle to travel from one spatial point (x') at one time (t') to another spatial point (x) at a later time (t). Consider a system with Hamiltonian . The Green's func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |