|
Reduced Dimensions Form
In biophysics and related fields, reduced dimension forms (RDFs) are unique on-off mechanisms for random walks that generate Two-state trajectory, two-state trajectories (see Fig. 1 for an example of a RDF and Fig. 2 for an example of a two-state trajectory). It has been shown that RDFs solve two-state trajectories, since only one RDF can be constructed from the data, where this property does not hold for on-off kinetic schemes, where many kinetic schemes can be constructed from a particular two-state trajectory (even from an ideal on-off trajectory). Two-state time trajectories are very common in measurements in chemistry, physics, and the biophysics of Single-molecule experiment, individual molecules (e.g. measurements of protein dynamics and Force spectroscopy, DNA and RNA dynamics, activity of ion channels, Enzyme, enzyme activity, quantum dots ), thus making RDFs an important tool in the analysis of data in these fields. Since RDFs are uniquely obtained from the data,O Flomenbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Biophysics
Biophysics is an interdisciplinary science that applies approaches and methods traditionally used in physics to study biological phenomena. Biophysics covers all scales of biological organization, from molecular to organismic and populations. Biophysical research shares significant overlap with biochemistry, molecular biology, physical chemistry, physiology, nanotechnology, bioengineering, computational biology, biomechanics, developmental biology and systems biology. The term ''biophysics'' was originally introduced by Karl Pearson in 1892. Roland Glaser. Biophysics: An Introduction'. Springer; 23 April 2012. . The term ''biophysics'' is also regularly used in academia to indicate the study of the physical quantities (e.g. electric current, temperature, stress, entropy) in biological systems. Other biological sciences also perform research on the biophysical properties of living organisms including molecular biology, cell biology, chemical biology, and bioche ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
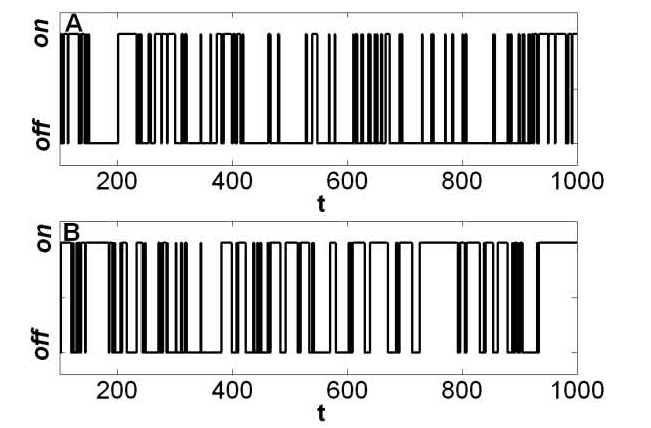
Two State Trajectory
A two-state trajectory (also termed two-state time trajectory or a trajectory with two states) is a dynamical signal that fluctuates between two distinct values: ON and OFF, open and closed, +/-, etc. Mathematically, the signal X(t) has, for every t, either the value X(t)=c_\mathrm or X(t)=c_\mathrm. In most applications, the signal is stochastic; nevertheless, it can have deterministic ON-OFF components. A completely deterministic two-state trajectory is a square wave. There are many ways one can create a two-state signal, e.g. flipping a coin repeatedly. A stochastic two-state trajectory is among the simplest stochastic processes. Extensions include: three-state trajectories, higher discrete state trajectories, and continuous trajectories in any dimension. Two state trajectories in biophysics, and related fields Two state trajectories are very common. Here, we focus on relevant trajectories in scientific experiments: these are seen in measurements in chemistry, physics, and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
WHAT RDF DOES
What or WHAT may refer to: * What, an English interrogative word * "What?", one of the Five Ws used in journalism Film and television * ''What!'' (film), also known as ''The Whip and the Body'', a 1963 Italian film directed by Mario Bava * ''What?'' (film), a 1972 film directed by Roman Polanski * "What?!", a 2019 episode of the TV series ''Barry'' * "What", the name of the second baseman in Abbott and Costello's comedy routine " Who's on First?" * "What?", the catchphrase of professional wrestler Stone Cold Steve Austin Music * ''what.'', a comedy/music album by Bo Burnham, 2013 * What Records, a UK record label specializing in punk and indie music * What? Records, a US record label Songs * "What" (song), by Melinda Marx, 1965 * "What?" (Rob Zombie song), 2009 * "What?" (SB19 song), 2021 * "What?", by 666 from ''The Soft Boys'' * "What", by Bassnectar from ''Vava Voom'' * "What?", by Corrosion of Conformity from ''Eye for an Eye'' * "What?", by the Move from ''Looking O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kinetic Scheme
In physics, chemistry and related fields, a kinetic scheme is a network of states and connections between them representing a dynamical process. Usually a kinetic scheme represents a Markovian process, while for non-Markovian processes generalized kinetic schemes are used. Figure 1 illustrates a kinetic scheme. A Markovian kinetic scheme Mathematical description A kinetic scheme is a network (a directed graph) of distinct states (although repetition of states may occur and this depends on the system), where each pair of states ''i'' and ''j'' are associated with directional rates, A_ (and A_). It is described with a master equation: a first-order differential equation for the probability \vec of a system to occupy each one its states at time ''t'' (element ''i'' represents state ''i''). Written in a matrix form, this states: \frac=\mathbf\vec, where \mathbf is the matrix of connections (rates) A_. In a Markovian kinetic scheme the connections are constant with respect to time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Microscopic Reversibility
The principle of microscopic reversibility in physics and chemistry is twofold: * First, it states that the microscopic detailed dynamics of particles and fields is time-reversible because the microscopic equations of motion are symmetric with respect to inversion in time (T-symmetry); * Second, it relates to the statistical description of the kinetics of macroscopic or mesoscopic systems as an ensemble of elementary processes: collisions, elementary transitions or reactions. For these processes, the consequence of the microscopic T-symmetry is: ''Corresponding to every individual process there is a reverse process, and in a state of equilibrium the average rate of every process is equal to the average rate of its reverse process.'' History of microscopic reversibility The idea of microscopic reversibility was born together with physical kinetics. In 1872, Ludwig Boltzmann represented kinetics of gases as statistical ensemble of elementary collisions.Boltzmann, L. (1964), Lectures on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rejection Sampling
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of exact simulation method. The method works for any distribution in \mathbb^m with a density. Rejection sampling is based on the observation that to sample a random variable in one dimension, one can perform a uniformly random sampling of the two-dimensional Cartesian graph, and keep the samples in the region under the graph of its density function. Note that this property can be extended to ''N''-dimension functions. Description To visualize the motivation behind rejection sampling, imagine graphing the probability density function (PDF) of a random variable onto a large rectangular board and throwing darts at it. Assume that the darts are uniformly distributed around the board. Now remove all of the darts that are outside the area und ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gillespie Algorithm
In probability theory, the Gillespie algorithm (or the Doob–Gillespie algorithm or stochastic simulation algorithm, the SSA) generates a statistically correct trajectory (possible solution) of a stochastic equation system for which the reaction rates are known. It was created by Joseph L. Doob and others (circa 1945), presented by Dan Gillespie in 1976, and popularized in 1977 in a paper where he uses it to simulate chemical or biochemical systems of reactions efficiently and accurately using limited computational power (see stochastic simulation). As computers have become faster, the algorithm has been used to simulate increasingly complex systems. The algorithm is particularly useful for simulating reactions within cells, where the number of reagents is low and keeping track of every single reaction is computationally feasible. Mathematically, it is a variant of a dynamic Monte Carlo method and similar to the kinetic Monte Carlo methods. It is used heavily in computational system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
PIC RDF
PIC or pic may refer to: Places * Penbay International Circuit, or PIC, a motor track circuit in Pingtung County, Taiwan * Pic River, in Ontario, Canada * Picayune (Amtrak station) (Amtrak station code PIC), Mississippi, United States * Pic, abbreviation for Pictor, a southern constellation * Pacific island countries People * Anna Pic (born 1978), French politician * Anne-Sophie Pic (born 1969), French cook * Charles Pic (born 1990), French Formula One driver * Maurice Pic (1866–1957), French entomologist * Tina Pic (born 1966), American racing cyclist Enterprises and organizations * PIC, a mark used by the former Phoenix Iron Company * Pickleball International Committee, a governing body for the sport of pickleball * Poison information center, a medical facility * Public Investment Corporation, a South African state-owned asset management firm Government and politics * Palestinian Information Center, a news website * Partido Independiente de Color, a former Cuban politi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Random Walk
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some Space (mathematics), mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating random walk hypothesis, stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Realizations of random walks can be obtained by Monte Carlo Simulation, Monte Carlo simulation. Lattice random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Dot
Quantum dots (QDs) or semiconductor nanocrystals are semiconductor particles a few nanometres in size with optical and electronic properties that differ from those of larger particles via quantum mechanical effects. They are a central topic in nanotechnology and materials science. When a quantum dot is illuminated by UV light, an electron in the quantum dot can be excited to a state of higher energy. In the case of a semiconducting quantum dot, this process corresponds to the transition of an electron from the valence band to the conduction band. The excited electron can drop back into the valence band releasing its energy as light. This light emission ( photoluminescence) is illustrated in the figure on the right. The color of that light depends on the energy difference between the discrete energy levels of the quantum dot in the conduction band and the valence band. In other words, a quantum dot can be defined as a structure on a semiconductor which is capable of confi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Enzyme
An enzyme () is a protein that acts as a biological catalyst by accelerating chemical reactions. The molecules upon which enzymes may act are called substrate (chemistry), substrates, and the enzyme converts the substrates into different molecules known as product (chemistry), products. Almost all metabolism, metabolic processes in the cell (biology), cell need enzyme catalysis in order to occur at rates fast enough to sustain life. Metabolic pathways depend upon enzymes to catalyze individual steps. The study of enzymes is called ''enzymology'' and the field of pseudoenzyme, pseudoenzyme analysis recognizes that during evolution, some enzymes have lost the ability to carry out biological catalysis, which is often reflected in their amino acid sequences and unusual 'pseudocatalytic' properties. Enzymes are known to catalyze more than 5,000 biochemical reaction types. Other biocatalysts include Ribozyme, catalytic RNA molecules, also called ribozymes. They are sometimes descr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |