|
Radial Parabolic Trajectory
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy). Under standard assumptions a body traveling along an escape orbit will coast along a parabolic trajectory to infinity, with velocity relative to the central body tending to zero, and therefore will never return. Parabolic trajectories are minimum-energy escape trajectories, separating positive-energy hyperbolic trajectories from negative-energy elliptic orbits. Velocity The orbital velocity (v) of a body travelling along parabolic trajectory can be computed as: :v = \sqrt where: *r is the radial distance of orbiting body from central body, *\mu is the standard gravitational parameter. At any positi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Escape Velocity
In celestial mechanics, escape velocity or escape speed is the minimum speed needed for a free, non- propelled object to escape from the gravitational influence of a primary body, thus reaching an infinite distance from it. It is typically stated as an ideal speed, ignoring atmospheric friction. Although the term "escape velocity" is common, it is more accurately described as a speed than a velocity because it is independent of direction; the escape speed increases with the mass of the primary body and decreases with the distance from the primary body. The escape speed thus depends on how far the object has already traveled, and its calculation at a given distance takes into account that without new acceleration it will slow down as it travels—due to the massive body's gravity—but it will never quite slow to a stop. A rocket, continuously accelerated by its exhaust, can escape without ever reaching escape speed, since it continues to add kinetic energy from its engine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Equation
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force. It was first derived by Johannes Kepler in 1609 in Chapter 60 of his ''Astronomia nova'', and in book V of his '' Epitome of Copernican Astronomy'' (1621) Kepler proposed an iterative solution to the equation. The equation has played an important role in the history of both physics and mathematics, particularly classical celestial mechanics. Equation Kepler's equation is where M is the mean anomaly, E is the eccentric anomaly, and e is the eccentricity. The 'eccentric anomaly' E is useful to compute the position of a point moving in a Keplerian orbit. As for instance, if the body passes the periastron at coordinates x = a(1 - e), y = 0, at time t = t_0, then to find out the position of the body at any time, you first calculate the mean anomaly M from the time and the mean motion n by the formula M = n(t - t_0), then solve the Kepler equation above t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
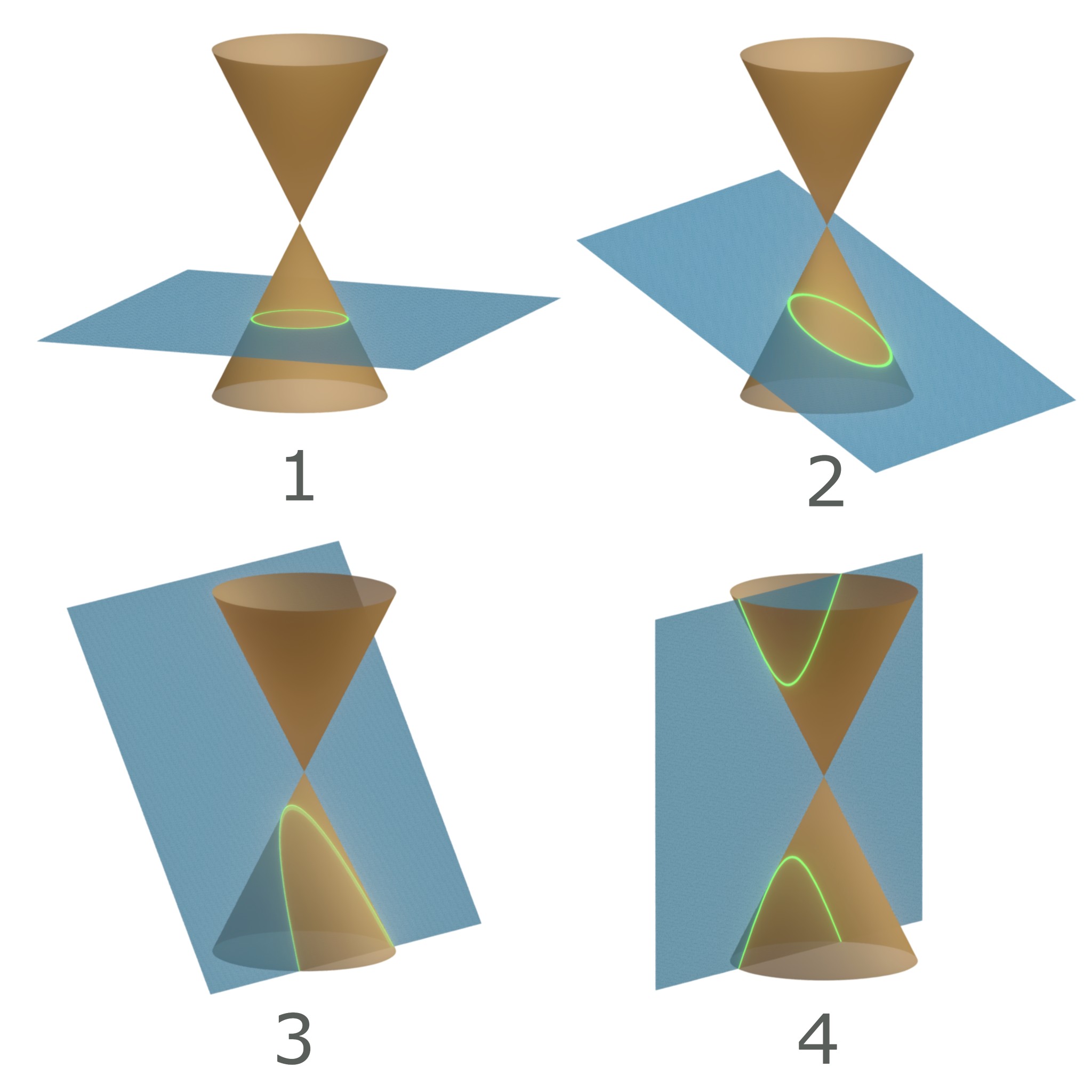
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Energy Conservation Equation
In astrodynamics, the ''vis-viva'' equation, also referred to as orbital-energy-invariance law, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy which applies when the only force acting on an object is its own weight. ''Vis viva'' (Latin for "living force") is a term from the history of mechanics, and it survives in this sole context. It represents the principle that the difference between the total work of the accelerating forces of a system and that of the retarding forces is equal to one half the ''vis viva'' accumulated or lost in the system while the work is being done. Equation For any Keplerian orbit (elliptic, parabolic, hyperbolic, or radial), the ''vis-viva'' equation is as follows: :v^2 = GM \left( - \right) where: * ''v'' is the relative speed of the two bodies * ''r'' is the distance between the two bodies centers of mass * ''a'' is the length of the semi-major axis ('' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Orbital Energy
In the gravitational two-body problem, the specific orbital energy \varepsilon (or vis-viva energy) of two orbiting bodies is the constant sum of their mutual potential energy (\varepsilon_p) and their total kinetic energy (\varepsilon_k), divided by the reduced mass. According to the orbital energy conservation equation (also referred to as vis-viva equation), it does not vary with time: \begin \varepsilon &= \varepsilon_k + \varepsilon_p \\ &= \frac - \frac = -\frac \frac \left(1 - e^2\right) = -\frac \end where *v is the relative orbital speed; *r is the orbital distance between the bodies; *\mu = (m_1 + m_2) is the sum of the standard gravitational parameters of the bodies; *h is the specific relative angular momentum in the sense of relative angular momentum divided by the reduced mass; *e is the orbital eccentricity; *a is the semi-major axis. It is expressed in MJ/kg or \frac. For an elliptic orbit the specific orbital energy is the neg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits). The true anomaly is usually denoted by the Greek letters or , or the Latin letter , and is usually restricted to the range 0–360° (0–2π). As shown in the image, the true anomaly is one of three angular parameters (''anomalies'') that defines a position along an orbit, the other two being the eccentric anomaly and the mean anomaly. Formulas From state vectors For elliptic orbits, the true anomaly can be calculated from orbital state vectors as: : \nu = \arccos ::(if then replace by ) where: * v is the orbital velocity vector of the orbiting body, * e is the eccentricity vector, * r is the orbital position vector (segment ''FP'' in the figure) of the orbiting bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbiting Body
In astrodynamics, an orbiting body is any physical body that orbits a more massive one, called the primary body. The orbiting body is properly referred to as the secondary body (m_2), which is less massive than the primary body (m_1). Thus, m_2 m_2. Under standard assumptions in astrodynamics, the barycenter of the two bodies is a focus of both orbits. An orbiting body may be a spacecraft (i.e. an artificial satellite) or a natural satellite, such as a planet, dwarf planet, moon, moonlet, asteroid, or comet. A system of two orbiting bodies is modeled by the Two-Body Problem and a system of three orbiting bodies is modeled by the Three-Body Problem. These problems can be generalized to an N-body problem. While there are a few analytical solutions to the n-body problem, it can be reduced to a 2-body system if the secondary body stays out of other bodies' Sphere of Influence and remains in the primary body's sphere of influence. See also *Barycenter *Double planet *Primary (a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Angular Momentum
In celestial mechanics, the specific relative angular momentum (often denoted \vec or \mathbf) of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative position and relative linear momentum, divided by the mass of the body in question. Specific relative angular momentum plays a pivotal role in the analysis of the two-body problem, as it remains constant for a given orbit under ideal conditions. "Specific" in this context indicates angular momentum per unit mass. The SI unit for specific relative angular momentum is square meter per second. Definition The specific relative angular momentum is defined as the cross product of the relative position vector \mathbf and the relative velocity vector \mathbf . \mathbf = \mathbf\times \mathbf = \frac where \mathbf is the angular momentum vector, defined as \mathbf \times m \mathbf. The \mathbf vector is always perpendicular to the instantaneo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Equation
In astrodynamics, an orbit equation defines the path of orbiting body m_2\,\! around central body m_1\,\! relative to m_1\,\!, without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic section (i.e. circular orbit, elliptic orbit, parabolic trajectory, hyperbolic trajectory, or radial trajectory) with the central body located at one of the two foci, or ''the'' focus ( Kepler's first law). If the conic section intersects the central body, then the actual trajectory can only be the part above the surface, but for that part the orbit equation and many related formulas still apply, as long as it is a freefall (situation of weightlessness). Central, inverse-square law force Consider a two-body system consisting of a central body of mass ''M'' and a much smaller, orbiting bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics of orbi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the center of the central mass perpendicular to the plane of motion. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version. Circular acceleration Transverse acceleration (perpendicular to velocity) causes change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates with respect to time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is orbital velocity of orbiting body, *r\, is radius of the circle * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |