|
Quadrature Of The Parabola
''Quadrature of the Parabola'' ( el, Τετραγωνισμὸς παραβολῆς) is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing that the area of a parabolic segment (the region enclosed by a parabola and a line) is \tfrac43 that of a certain inscribed triangle. It is one of the best-known works of Archimedes, in particular for its ingenious use of the method of exhaustion and in the second part of a geometric series. Archimedes dissects the area into infinitely many triangles whose areas form a geometric progression. He then computes the sum of the resulting geometric series, and proves that this is the area of the parabolic segment. This represents the most sophisticated use of a '' reductio ad absurdum'' argument in ancient Greek mathematics, and Archimedes' solution remained unsurpassed until the developm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Parabolic Segment
Parabolic usually refers to something in a shape of a parabola, but may also refer to a parable. Parabolic may refer to: *In mathematics: **In elementary mathematics, especially elementary geometry: **Parabolic coordinates ** Parabolic cylindrical coordinates ** parabolic Möbius transformation ** Parabolic geometry (other) ** Parabolic spiral ** Parabolic line **In advanced mathematics: ***Parabolic cylinder function ***Parabolic induction ***Parabolic Lie algebra ***Parabolic partial differential equation *In physics: **Parabolic trajectory *In technology: **Parabolic antenna **Parabolic microphone **Parabolic reflector **Parabolic trough - a type of solar thermal energy collector **Parabolic flight - a way of achieving weightlessness ** Parabolic action, or parabolic bending curve - a term often used to refer to a progressive bending curve in fishing rods. *In commodities and stock markets: **Parabolic SAR In stock and securities market technical analysis, parabolic SAR ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Menaechmus
:''There is also a Menaechmus in Plautus' play, ''The Menaechmi''.'' Menaechmus ( el, Μέναιχμος, 380–320 BC) was an ancient Greek mathematician, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube using the parabola and hyperbola. Life and work Menaechmus is remembered by mathematicians for his discovery of the conic sections and his solution to the problem of doubling the cube. Menaechmus likely discovered the conic sections, that is, the ellipse, the parabola, and the hyperbola, as a by-product of his search for the solution to the Delian problem. Menaechmus knew that in a parabola y2 = ''L''x, where ''L'' is a constant called the ''latus rectum'', although he was not aware of the fact that any equation in two unknowns determines a curve. He ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Archimedean Property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some algebraic structures, such as ordered or normed groups, and fields. The property, typically construed, states that given two positive numbers ''x'' and ''y'', there is an integer ''n'' such that ''nx'' > ''y''. It also means that the set of natural numbers is not bounded above. Roughly speaking, it is the property of having no ''infinitely large'' or ''infinitely small'' elements. It was Otto Stolz who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes’ '' On the Sphere and Cylinder''. The notion arose from the theory of magnitudes of Ancient Greece; it still plays an important role in modern mathematics such as David Hilbert's axioms for geometry, and the theories of ordered groups, ordered fields, and local fields. An algebraic structure in which any two non-zero elements are ''compa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Partial Sum
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Quadrature Parabola Relative Sizes
Quadrature may refer to: In signal processing: *Quadrature amplitude modulation (QAM), a modulation method of using both an (in-phase) carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier *Quadrature phase, oscillations that are said to be ''in quadrature'' if they are separated in phase by 90° (/2, or /4) *Quadrature filter, the analytic signal of a real-valued filter * Quadrature phase-shift keying (QPSK), a phase-shift keying of using four quadrate points on the constellation diagram, equispaced around a circle In mathematics: * Quadrature (mathematics), drawing a square with the same area as a given plane figure (''squaring'') or computing that area ** Quadrature of the circle * Numerical integration is often called 'numerical quadrature' or simply 'quadrature' ** Gaussian quadrature, a special case of numerical integration * Formerly, a synonym for "integral" ** Integral ** Antiderivative * Addition in quadrature, combini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Analytic Geometry
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry. Analytic geometry is used in physics and engineering, and also in aviation, Aerospace engineering, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including Algebraic geometry, algebraic, Differential geometry, differential, Discrete geometry, discrete and computational geometry. Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space. As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometric shapes in a numerical way and extracting numerical information from shapes' numerical defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Parabolic Segment Dissection
Parabolic usually refers to something in a shape of a parabola, but may also refer to a parable. Parabolic may refer to: *In mathematics: **In elementary mathematics, especially elementary geometry: **Parabolic coordinates **Parabolic cylindrical coordinates ** parabolic Möbius transformation ** Parabolic geometry (other) ** Parabolic spiral ** Parabolic line **In advanced mathematics: ***Parabolic cylinder function ***Parabolic induction ***Parabolic Lie algebra ***Parabolic partial differential equation *In physics: **Parabolic trajectory *In technology: **Parabolic antenna **Parabolic microphone **Parabolic reflector **Parabolic trough - a type of solar thermal energy collector **Parabolic flight - a way of achieving weightlessness ** Parabolic action, or parabolic bending curve - a term often used to refer to a progressive bending curve in fishing rods. *In commodities and stock markets: **Parabolic SAR In stock and securities market technical analysis, parabolic SAR ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Conic Sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Euclid
Euclid (; grc-gre, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved new innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the philosophers Proclus and Pappus of Alexandria many centuries later. Until the early Renaissance he was often mistaken for the earlier philosopher Euclid of Megara, causing his biograph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
On The Equilibrium Of Planes
''On the Equilibrium of Planes'' ( grc, Περὶ ἐπιπέδων ἱσορροπιῶν, translit=perí epipédōn isorropiôn) is a treatise by Archimedes in two volumes. The first book contains a proof of the law of the lever and culminates with propositions on the centre of gravity of the triangle and the trapezium. The second book, which contains ten propositions, examines the centres of gravity of parabolic segments. According to Pappus of Alexandria, Archimedes' work on levers caused him to say: "Give me a place to stand on, and I will move the Earth" ( grc, δός μοί ποῦ στῶ καὶ κινῶ τὴν γῆν, translit=dṓs moi poû stṓ kaí kinô tḗn gên, links=no), though other ancient testimonia are ambiguous regarding the context of the saying. Overview The lever and its properties were already well known before the time of Archimedes, and he was not the first to provide an analysis of the principle involved. The earlier '' Mechanical Problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
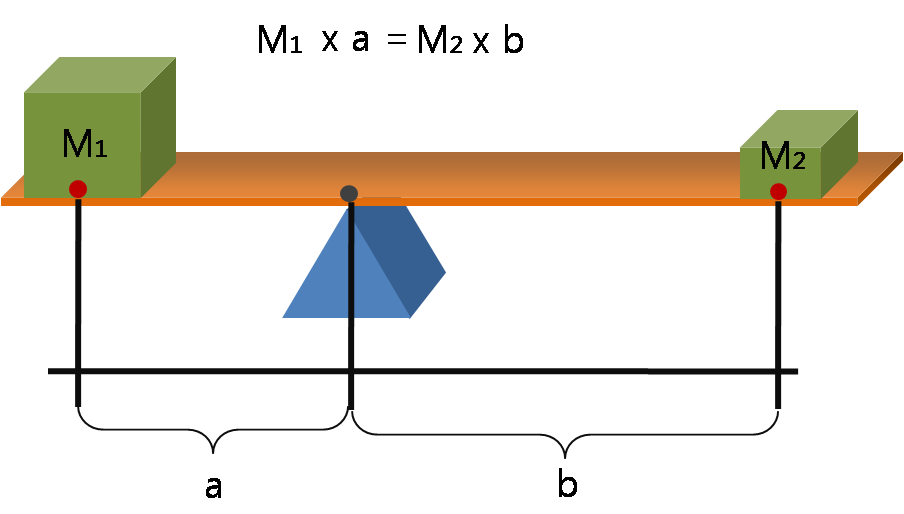 |
Lever
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or '' fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load and effort, the lever is divided into three types. Also, leverage is mechanical advantage gained in a system. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage. The ratio of the output force to the input force is the mechanical advantage of the lever. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English around 1300 from Old French, in which the word was ''levier''. This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to the Latin ''levare'', itself from the adjective ''levis'', meaning "light" (as in "not heavy") ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |