Quaternions And Spatial Rotation
unit vector, Unit quaternions, known as versor, ''versors'', provide a convenient mathematics, mathematical notation for representing spatial Orientation (geometry), orientations and rotations of elements in three dimensional space. Specifically, they encode information about an Axis–angle representation, axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, Presented at SIGGRAPH '85. computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and Texture (crystalline), crystallographic texture analysis. When used to represent rotation, unit quaternions are also called rotation quaternions as they represent the 3D rotation group. When used to represent an Orientation (geometry), orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. A spatial rotation around a fixed point of \theta radians ab ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

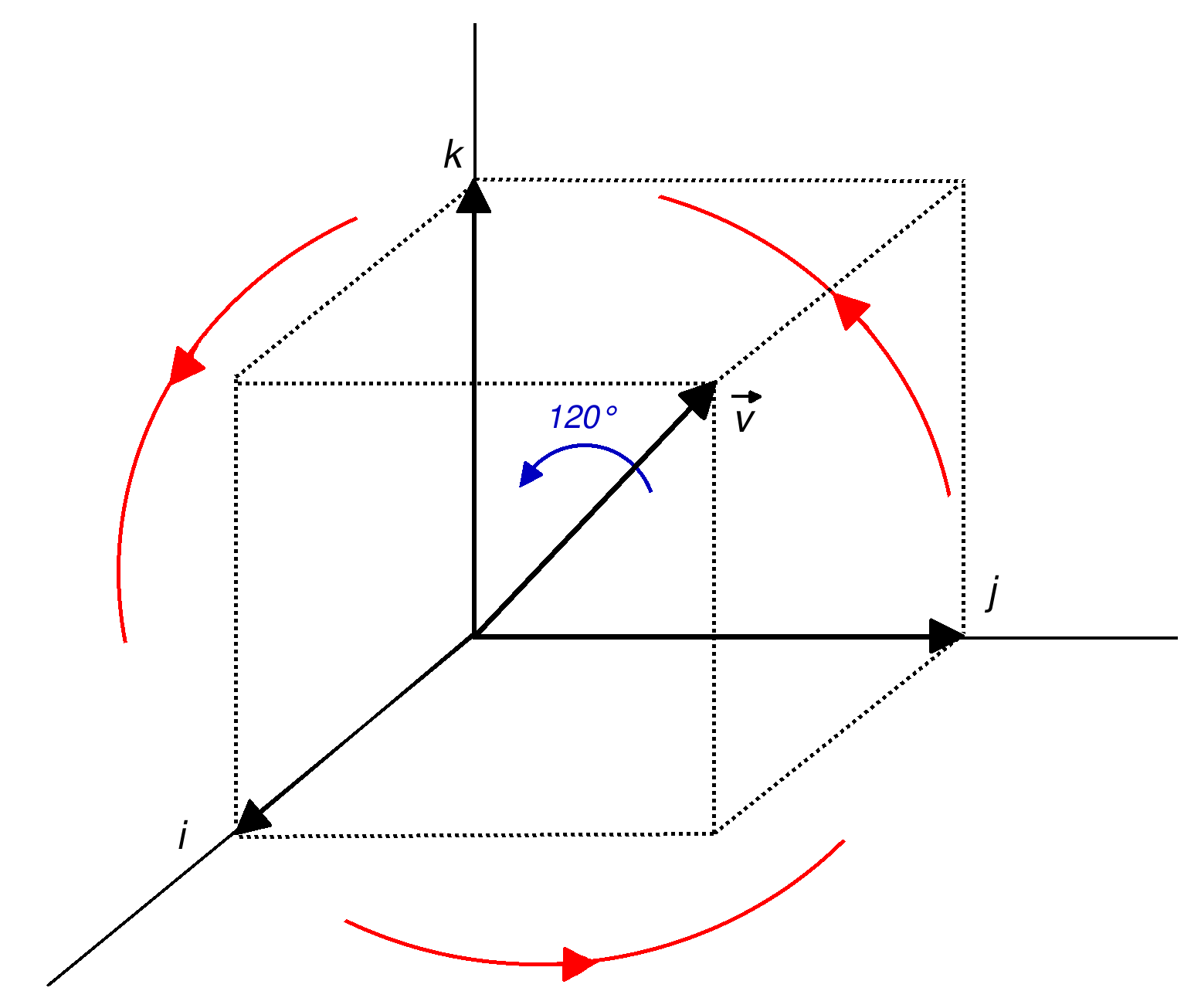
Unit Vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''direction vector'', commonly denoted as d, is used to describe a unit vector being used to represent spatial direction and relative direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac where , u, is the norm (or length) of u. The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. Unit vectors are often chosen to form the basis of a vector space, and every vector in the space may be written as a linear combination of unit vectors. Orthogonal coordinates Cartesian coordinates Unit vectors may b ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]