|
Quasiperiodic Function
In mathematics, a quasiperiodic function is a function (mathematics), function that has a certain similarity to a periodic function. A function f is quasiperiodic with quasiperiod \omega if f(z + \omega) = g(z,f(z)), where g is a "''simpler''" function than f. What it means to be "''simpler''" is vague. A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation: : f(z + \omega) = f(z) + C Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation: : f(z + \omega) = C f(z) An example of this is the theta function, Jacobi theta function, where :\vartheta(z+\tau;\tau) = e^{-2\pi iz - \pi i\tau}\vartheta(z;\tau), shows that for fixed \tau it has quasiperiod \tau; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass elliptic functions, Weierstrass ''℘'' funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
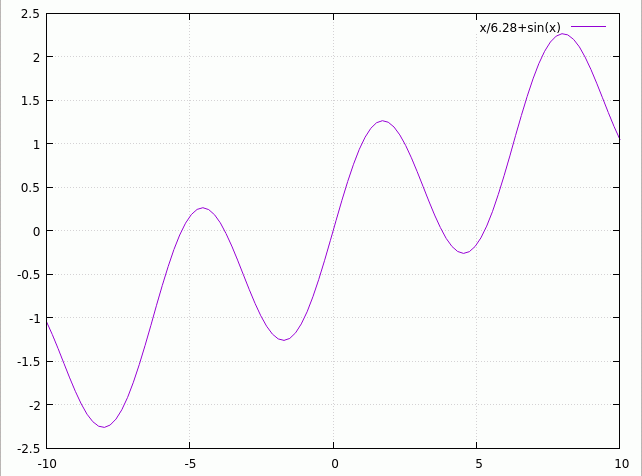
Arithmetic Quasiperiodic Function
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theta Function
In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory. The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables (conventionally called ), a theta function has a property expressing its behavior with respect to the addition of a period of the associated elliptic functions, making it a quasiperiodic function. In the abstract theory this quasiperiodicity comes from the cohomology class of a line bundle on a complex torus, a condition of descent. One interpretation of theta functions when dealing with the heat equation is that "a theta function is a special function that describes the evolution of temperature on a segment domain subject to certain boundary conditions". Throughout this article, (e^)^ should b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Sigma Function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass. The relation between the sigma, zeta, and \wp functions is analogous to that between the sine, cotangent, and squared cosecant functions: the logarithmic derivative of the sine is the cotangent, whose derivative is negative the squared cosecant. Weierstrass sigma function The Weierstrass sigma function associated to a two-dimensional lattice \Lambda\subset\Complex is defined to be the product : \begin \operatorname&=z\prod_ \left(1-\frac\right) e^ \\ &=z\prod_^\infty \left(1-\frac\right) e^ \end where \Lambda^ denotes \Lambda-\ or \ are a ''fundamental pair of periods''. Through careful manipulation of the Weierstrass factorization theorem as it relates also to the sine function, another potentially more manageable infinite product definition is : \operatorname=\frace^\sin\prod_^\infty\left(1-\frac\rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Definition Let \omega_1,\omega_2\in\mathbb be two complex numbers that are linearly independent over \mathbb and let \Lambda:=\mathbb\omega_1+\mathbb\omega_2:=\ be the lattice generated by those numbers. Then the \wp-function is defined as follows: \weierp(z,\omega_1,\omega_2):=\weierp(z,\Lambda) := \frac + \sum_\left(\frac 1 - \frac 1 \right). This series converges locally uniformly absolutely in \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Zeta Function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass. The relation between the sigma, zeta, and \wp functions is analogous to that between the sine, cotangent, and squared cosecant functions: the logarithmic derivative of the sine is the cotangent, whose derivative is negative the squared cosecant. Weierstrass sigma function The Weierstrass sigma function associated to a two-dimensional lattice \Lambda\subset\Complex is defined to be the product : \begin \operatorname&=z\prod_ \left(1-\frac\right) e^ \\ &=z\prod_^\infty \left(1-\frac\right) e^ \end where \Lambda^ denotes \Lambda-\ or \ are a ''fundamental pair of periods''. Through careful manipulation of the Weierstrass factorization theorem as it relates also to the sine function, another potentially more manageable infinite product definition is : \operatorname=\frace^\sin\prod_^\infty\left(1-\frac\rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A function with period will repeat on intervals of length , and these intervals are sometimes also referred to as periods of the function. Geometrically, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Periodic Function
In mathematics, an almost periodic function is, loosely speaking, a function of a real number that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov, Hermann Weyl and Abram Samoilovitch Besicovitch, amongst others. There is also a notion of almost periodic functions on locally compact abelian groups, first studied by John von Neumann. Almost periodicity is a property of dynamical systems that appear to retrace their paths through phase space, but not exactly. An example would be a planetary system, with planets in orbits moving with periods that are not commensurable (i.e., with a period vector that is not proportional to a vector of integers). A theorem of Kronecker from diophantine approximation can be used to show that any particular configuration that occurs once, will recur to within any specified accuracy: if we wait long eno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodicity
Quasiperiodicity is the property of a system that displays irregular periodicity. Periodic behavior is defined as recurring at regular intervals, such as "every 24 hours". Quasiperiodic behavior is a pattern of recurrence with a component of unpredictability that does not lend itself to precise measurement. It is different from the mathematical concept of an almost periodic function, which has increasing regularity over multiple periods. The mathematical definition of quasiperiodic function is a completely different concept; the two should not be confused. Climatology Climate oscillations that appear to follow a regular pattern but which do not have a fixed period are called ''quasiperiodic''. Within a dynamical system such as the ocean-atmosphere oscillations may occur regularly, when they are forced by a regular external forcing: for example, the familiar winter-summer cycle is forced by variations in sunlight from the (very close to perfectly) periodic motion of the earth around ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is in rough terms the type of motion executed by a dynamical system containing a finite number (two or more) of incommensurable frequencies. That is, if we imagine that the phase space is modelled by a torus ''T'' (that is, the variables are periodic like angles), the trajectory of the system is modelled by a curve on ''T'' that wraps around the torus without ever exactly coming back on itself. A quasiperiodic function on the real line is the type of function (continuous, say) obtained from a function on ''T'', by means of a curve :''R'' → ''T'' which is linear (when lifted from ''T'' to its covering Euclidean space), by composition. It is therefore oscillating, with a finite number of underlying frequencies. (NB the sense in which theta functions and the Weierstrass zeta function in complex analysis are said to have quasi-periods with respect to a period lattice is something distinct from this.) The theory of alm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PlanetMath
PlanetMath is a free, collaborative, mathematics online encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org, Ltd". PlanetMath was started when the popular free online mathematics encyclopedia MathWorld was temporarily taken offline for 12 months by a court injunction as a result of the CRC Press lawsuit against the Wolfram Research company and its employee (and MathWorld's author) Eric Weisstein. Materials The main PlanetMath focus is on encyclopedic entries. It formerly operated a self-hosted forum, but now encourages discussion via Gitter. , the encyclopedia hosted about 9,289 entries and over 16,258 ''concepts'' (a concept may be for example a specific notion defined within a more general entry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
