|
Quartic Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros. The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscates and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bullet-nose Curve
In mathematics, a bullet-nose curve is a unicursal quartic curve with three inflection points, given by the equation :a^2y^2-b^2x^2=x^2y^2 \, The bullet curve has three double points in the real projective plane, at and , and , and and , and is therefore a unicursal (rational) curve of genus Genus ( plural genera ) is a taxonomic rank used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In the hierarchy of biological classification, genus com ... zero. If :f(z) = \sum_^ z^ = z+2z^3+6z^5+20z^7+\cdots then :y = f\left(\frac\right)\pm 2b\ are the two branches of the bullet curve at the origin. References * Plane curves Algebraic curves {{algebraic-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamé's Special Quartic
Lamé's special quartic, named after Gabriel Lamé, is the graph of the equation :x^4 + y^4 = r^4 where r > 0. It looks like a rounded square with "sides" of length 2r and centered on the origin. This curve is a squircle centered on the origin, and it is a special case of a superellipse.. Because of Pierre de Fermat's only surviving proof, that of the ''n'' = 4 case of Fermat's Last Theorem, if ''r'' is rational Rationality is the quality of being guided by or based on reasons. In this regard, a person acts rationally if they have a good reason for what they do or a belief is rational if it is based on strong evidence. This quality can apply to an abili ... there is no non-trivial rational point (''x'', ''y'') on this curve (that is, no point for which both ''x'' and ''y'' are non-zero rational numbers). References Equations {{algebraic-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squircle
A squircle is a shape intermediate between a square and a circle. There are at least two definitions of "squircle" in use, the most common of which is based on the superellipse. The word "squircle" is a portmanteau of the words "square" and "circle". Squircles have been applied in design and optics. Superellipse-based squircle In a Cartesian coordinate system, the superellipse is defined by the equation \left, \frac\^n + \left, \frac\^n = 1, where and are the semi-major and semi-minor axes, and are the and coordinates of the centre of the ellipse, and is a positive number. The squircle is then defined as the superellipse with and . Its equation is: \left(x - a\right)^4 + \left(y - b\right)^4 = r^4 where is the minor radius of the squircle. Compare this to the equation of a circle. When the squircle is centred at the origin, then , and it is called Lamé's special quartic. The area inside the squircle can be expressed in terms of the gamma function as \mathrm = 4 r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spiric Section
In geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form :(x^2+y^2)^2=dx^2+ey^2+f. \, Equivalently, spiric sections can be defined as bicircular quartic curves that are symmetric with respect to the ''x'' and ''y''-axes. Spiric sections are included in the family of toric sections and include the family of hippopedes and the family of Cassini ovals. The name is from σπειρα meaning torus in ancient Greek. A spiric section is sometimes defined as the curve of intersection of a torus and a plane parallel to its rotational symmetry axis. However, this definition does not include all of the curves given by the previous definition unless imaginary planes are allowed. Spiric sections were first described by the ancient Greek geometer Perseus in roughly 150 BC, and are assumed to be the first toric sections to be described. The name ''spiric'' is due to the ancient notation ''spira'' of a torus., Wilbur R. Kn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lüroth Quartic
In mathematics, a Lüroth quartic is a nonsingular quartic plane curve containing the 10 vertices of a complete pentalateral. They were introduced by . showed that the Lüroth quartics form an open subset of a degree 54 hypersurface In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidea ..., called the Lüroth hypersurface, in the space P14 of all quartics. proved that the moduli space of Lüroth quartics is rational. References * * * {{DEFAULTSORT:Luroth Quartic Algebraic curves ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval. A limaçon is a bicircular rational plane algebraic curve of degree 4. History The earliest formal research on limaçons is generally attributed to Étienne Pascal, father ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
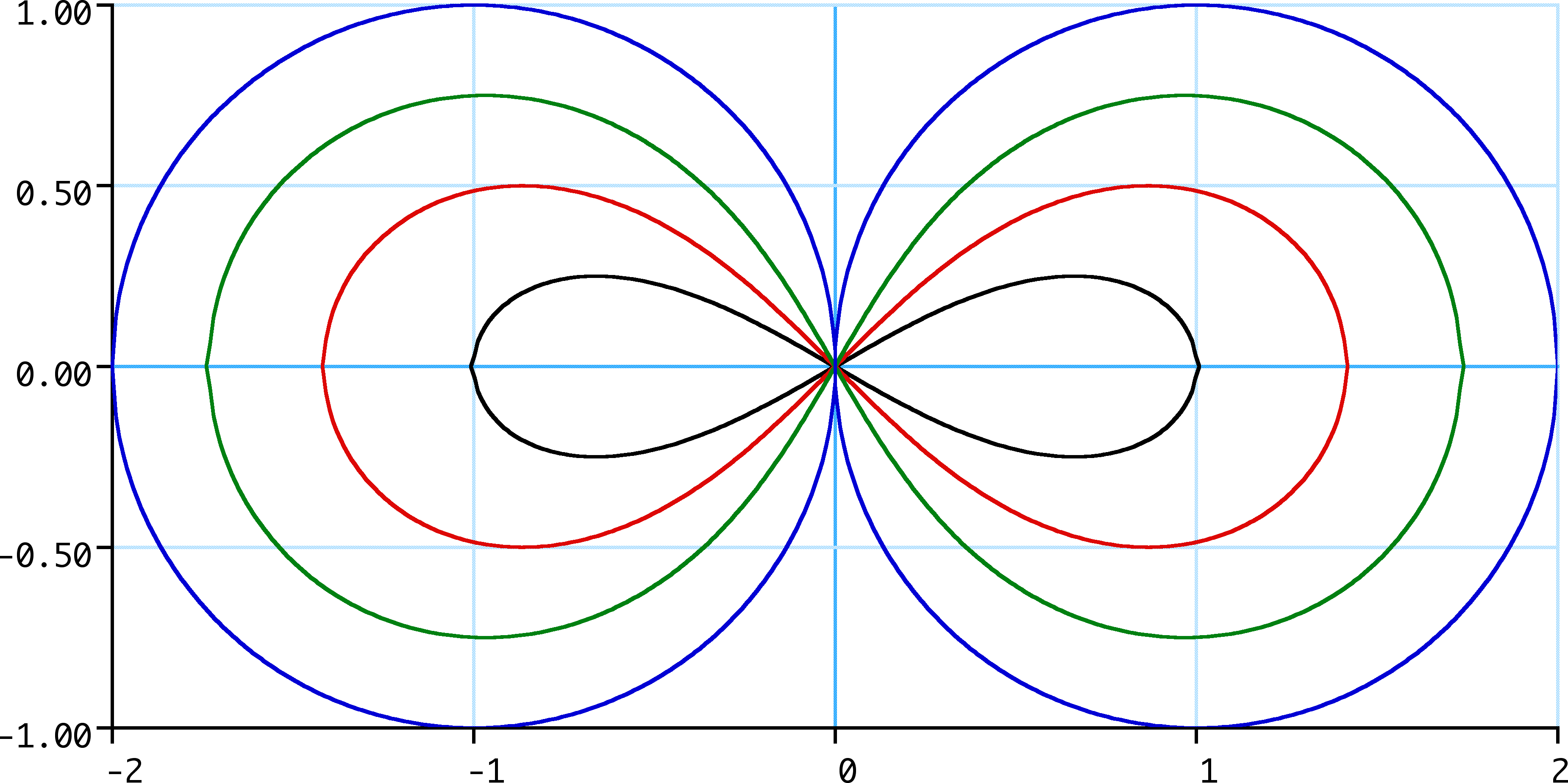
Lemniscate Of Gerono
In algebraic geometry, the lemniscate of Gerono, or lemniscate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero and is a lemniscate curve shaped like an \infty symbol, or figure eight. It has equation :x^4-x^2+y^2 = 0. It was studied by Camille-Christophe Gerono. Parameterization Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is :x = \frac,\ y = \frac. Another representation is :x = \cos \varphi,\ y = \sin\varphi\,\cos\varphi = \sin(2\varphi)/2 which reveals that this lemniscate is a special case of a Lissajous figure. Dual curve The dual curve (see Plücker formula In mathematics, a Plücker formula, named after Julius Plücker, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curves to corresponding invariants of their du ...), pictured below, has therefore a somewhat different character ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from , which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4. This lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse, which is the locus of points for which the sum of the distances to each of two fixed ''focal points'' is a constant. A Cassini oval, by contrast, is the locus of points for which the ''product'' of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli. This curve can be obtained as the inverse transform of a hyperbola, with the inversion circle centered at the center of the hyperbola (bisector o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate
In algebraic geometry, a lemniscate is any of several figure-eight or -shaped curves. The word comes from the Latin "''lēmniscātus''" meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbons",. or which alternatively may refer to the wool from which the ribbons were made. Curves that have been called a lemniscate include three quartic plane curves: the hippopede or lemniscate of Booth, the lemniscate of Bernoulli, and the lemniscate of Gerono. The study of lemniscates (and in particular the hippopede) dates to ancient Greek mathematics, but the term "lemniscate" for curves of this type comes from the work of Jacob Bernoulli in the late 17th century. History and examples Lemniscate of Booth The consideration of curves with a figure-eight shape can be traced back to Proclus, a Greek Neoplatonist philosopher and mathematician who lived in the 5th century AD. Proclus considered the cross-sections of a torus by a plane parallel to the axis of the tor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kampyle Of Eudoxus
The Kampyle of Eudoxus (Greek: καμπύλη ραμμή meaning simply "curved ine curve") is a curve with a Cartesian equation of :x^4 = a^2(x^2+y^2), from which the solution ''x'' = ''y'' = 0 is excluded. Alternative parameterizations In polar coordinates, the Kampyle has the equation :r = a\sec^2\theta. Equivalently, it has a parametric representation as :x=a\sec(t), \quad y=a\tan(t)\sec(t). History This quartic curve was studied by the Greek astronomer and mathematician Eudoxus of Cnidus (c. 408 BC – c.347 BC) in relation to the classical problem of doubling the cube. Properties The Kampyle is symmetric about both the ''x''- and ''y''-axes. It crosses the ''x''-axis at (±''a'',0). It has inflection points at :\left(\pm a\frac,\pm a\frac\right) (four inflections, one in each quadrant). The top half of the curve is asymptotic to x^2/a-a/2 as x \to \infty, and in fact can be written as :y = \frac\sqrt = \frac - \frac \sum_^\infty C_n\left(\frac\right)^, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hippopede
In geometry, a hippopede () is a plane curve determined by an equation of the form :(x^2+y^2)^2=cx^2+dy^2, where it is assumed that and since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular, rational, algebraic curves of degree 4 and symmetric with respect to both the and axes. Special cases When ''d'' > 0 the curve has an oval form and is often known as an oval of Booth, and when the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after 19th-century mathematician James Booth who studied them. Hippopedes were also investigated by Proclus (for whom they are sometimes called Hippopedes of Proclus) and Eudoxus. For , the hippopede corresponds to the lemniscate of Bernoulli. Definition as spiric sections Hippopedes can be defined as the curve formed by the intersection of a torus and a plane, where the plane is parallel to the axis of the to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
