|
Quantum Magnetism
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory and computability theory in theoretical computer science. The theory of spin models is a far reaching and unifying topic that cuts across many fields. Introduction In ordinary materials, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction. Ferromagnetic materials below their Curie temperature, however, exhibit magnetic domains in which the atomic dipole moments are locally aligned, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary "magnets" with which we are all familiar. The study of the behavior of such "spin models" is a thriving area of research in con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a mathematical model Mathematical models can take many forms, including dynamical systems, statisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kuramoto Model
The Kuramoto model (or Kuramoto–Daido model), first proposed by , is a mathematical model used to describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological oscillators, and it has found widespread applications in areas such as neuroscience and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions, followed his model. The model makes several assumptions, including that there is weak coupling, that the oscillators are identical or nearly identical, and that interactions depend sinusoidally on the phase difference between each pair of objects. Definition In the most popular version of the Kuramoto model, each of the oscillators is considered to have its own intrinsic natural frequency \omega_i, and each is coupled equally to all other oscillators ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
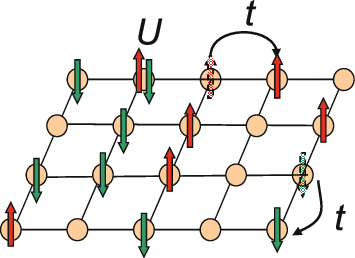
J1 J2 Model
The J1–J2 model is a quantum spin model like the Heisenberg model but also includes a term for the interaction between next-nearest neighbor spins. Hamiltonian In this model, the term J_1 represents the usual nearest-neighbor interaction as seen in the Heisenberg model, and J_2 represents the exchange interaction to the ''next'' nearest-neighbor. : \hat H = J_1 \sum_\vec S_i \cdot \vec S_j + J_2 \sum_ \vec S_i \cdot \vec S_j See also *Spin model *Heisenberg model (quantum) *Hubbard model *t-J model *Majumdar–Ghosh model The Majumdar–Ghosh model is a one-dimensional quantum Heisenberg spin model in which the nearest-neighbour antiferromagnetic exchange interaction is twice as strong as the next-nearest-neighbour interaction. It is a special case of the more gen ... References * * * * *{{cite journal, last1=Majumdar, first1=Chanchal K., last2=Ghosh, first2=Dipan K., title=On Next‐Nearest‐Neighbor Interaction in Linear Chain. II, journal=Journal of Mathematical Physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hubbard Model
The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed to be in the lowest Bloch band, and long-range interactions between the particles can be ignored. If interactions between particles at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Model (classical)
The Classical Heisenberg model, developed by Werner Heisenberg, is the n = 3 case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena. Definition It can be formulated as follows: take a d-dimensional lattice, and a set of spins of the unit length :\vec_i \in \mathbb^3, , \vec_i, =1\quad (1), each one placed on a lattice node. The model is defined through the following Hamiltonian: : \mathcal = -\sum_ \mathcal_ \vec_i \cdot \vec_j\quad (2) with : \mathcal_ = \begin J & \mboxi, j\mbox \\ 0 & \mbox\end a coupling between spins. Properties * The general mathematical formalism used to describe and solve the Heisenberg model and certain generalizations is developed in the article on the Potts model. * In the continuum limit the Heisenberg model (2) gives the following equation of motion :: \vec_=\vec\wedge \vec_. :This equation is called the continuous classical Heisenberg ferromagnet equation or shortly Heisenberg model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ANNNI Model
In statistical physics, the axial (or anisotropic) next-nearest neighbor Ising model, usually known as the ANNNI model, is a variant of the Ising model in which competing ferromagnetic and antiferromagnetic exchange interactions couple spins at nearest and next-nearest neighbor sites along one of the crystallographic axes of the lattice. The model is a prototype for complicated spatially modulated magnetic superstructures in crystals. To describe experimental results on magnetic orderings in erbium, the model was introduced in 1961 by Roger Elliott from the University of Oxford, . The model has given its name in 1980 by Michael E. Fisher and Walter Selke., who analysed it first by Monte Carlo methods, and then by low temperature series expansions, showing the fascinating complexity of its phase diagram, including devil's staircases and a Lifshitz point. Indeed, it provides, for two- and three-dimensional systems, a theoretical basis for understanding numerous experimental obser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says something like or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as ''noncommutative operations''. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept that under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Observables
In physics, an observable is a physical quantity that can be measured. Examples include position and momentum. In systems governed by classical mechanics, it is a real-valued "function" on the set of all possible system states. In quantum physics, it is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum physics, observables manifest as linear operators on a Hilbert space representing the state space of quantum states. The ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Chuang
Isaac L. Chuang is an American electrical engineer and physicist. He leads the quanta research group at the Center for Ultracold Atoms at Massachusetts Institute of Technology (MIT). He received his undergraduate degrees in physics (1990) and electrical engineering (1991) and master's in electrical engineering (1991) at MIT.Copsey, D.; Oskin, M.; Impens, F.; Metodiev, T.; Cross, A.; Chong, F.T.; Chuang, I.L.; Kubiatowicz, J., "Toward a scalable, silicon-based quantum computing architecture," IEEE Journal of Selected Topics in Quantum Electronics, vol.9, no.6, pp. 1552–1569, Nov.-Dec. 2003, In 1997 he received his PhD in electrical engineering from Stanford University. Chuang is one of the pioneers of Nuclear magnetic resonance quantum computer, NMR quantum computing. Since 2003, Chuang has focused his attention on trapped ion approaches to quantum computing, as the field of liquid state NMR quantum computing fell out of favor due to limitations on its scalability beyond tens of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |