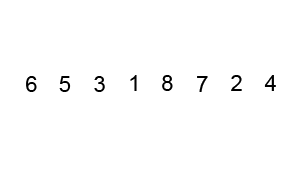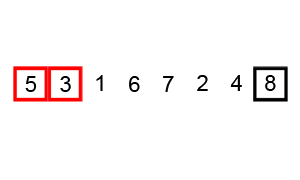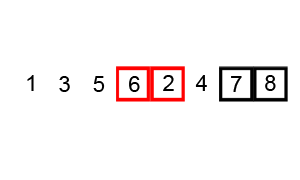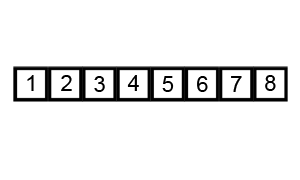|
Quadratic Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Computational Complexity
Comparison or comparing is the act of evaluating two or more things by determining the relevant, comparable characteristics of each thing, and then determining which characteristics of each are Similarity (psychology), similar to the other, which are Difference (philosophy), different, and to what degree. Where characteristics are different, the differences may then be evaluated to determine which thing is best suited for a particular purpose. The description of similarities and differences found between the two things is also called a comparison. Comparison can take many distinct forms, varying by field: To compare things, they must have characteristics that are similar enough in relevant ways to merit comparison. If two things are too different to compare in a useful way, an attempt to compare them is colloquially referred to in English as "comparing apples and oranges." Comparison is widely used in society, in science and the arts. General usage Comparison is a natural act ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Priority Queue
In computer science, a priority queue is an abstract data type similar to a regular queue (abstract data type), queue or stack (abstract data type), stack abstract data type. In a priority queue, each element has an associated ''priority'', which determines its order of service. Priority queue serves highest priority items first. Priority values have to be instances of an ordered data type, and higher priority can be given either to the lesser or to the greater values with respect to the given order relation. For example, in Java (programming language), Java standard library, ''PriorityQueues the least elements with respect to the order have the highest priority. This implementation detail is without much practical significance, since passing to the converse relation, opposite order relation turns the least values into the greatest, and vice versa. While priority queues are often implemented using Heap (data structure) , heaps, they are conceptually distinct. A priority queue can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bubble Sort
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the input list element by element, comparing the current element with the one after it, Swap (computer science), swapping their values if needed. These passes through the list are repeated until no swaps have to be performed during a pass, meaning that the list has become fully sorted. The algorithm, which is a comparison sort, is named for the way the larger elements "bubble" up to the top of the list. It performs poorly in real-world use and is used primarily as an educational tool. More efficient algorithms such as quicksort, timsort, or merge sort are used by the sorting libraries built into popular programming languages such as Python and Java. History The earliest description of the bubble sort algorithm was in a 1956 paper by mathematician and actuary Edward Harry Friend, ''Sorting on electronic computer systems'', published in the third issue of the third volume ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Evaluation
In mathematics and computer science, polynomial evaluation refers to computation of the value of a polynomial when its indeterminates are substituted for some values. In other words, evaluating the polynomial P(x_1, x_2) = 2x_1x_2 + x_1^3 + 4 at x_1=2, x_2=3 consists of computing P(2,3)= 2\cdot 2\cdot 3 + 2^3+4=24. See also For evaluating the univariate polynomial a_nx^n+a_x^+\cdots +a_0, the most naive method would use n multiplications to compute a_n x^n, use n-1 multiplications to compute a_ x^ and so on for a total of \tfrac multiplications and n additions. Using better methods, such as Horner's rule, this can be reduced to n multiplications and n additions. If some preprocessing is allowed, even more savings are possible. Background This problem arises frequently in practice. In computational geometry, polynomials are used to compute function approximations using Taylor polynomials. In cryptography and hash tables, polynomials are used to compute ''k''-independent has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by Matrix decomposition, factorizing the DFT matrix into a product of Sparse matrix, sparse (mostly zero) factors. As a result, it manages to reduce the Computational complexity theory, complexity of computing the DFT from O(n^2), which arises if one simply applies the definition of DFT, to O(n \log n), where is the data size. The difference in speed can be enormous, especially for long data sets where may be in the thousands or millions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation (often a "less than or equal to" operator or a three-way comparison) that determines which of two elements should occur first in the final sorted list. The only requirement is that the operator forms a total preorder over the data, with: # if ''a'' ≤ ''b'' and ''b'' ≤ ''c'' then ''a'' ≤ ''c'' (transitivity) # for all ''a'' and ''b'', ''a'' ≤ ''b'' or ''b'' ≤ ''a'' ( connexity). It is possible that both ''a'' ≤ ''b'' and ''b'' ≤ ''a''; in this case either may come first in the sorted list. In a stable sort, the input order determines the sorted order in this case. Comparison sorts studied in the literature are "comparison-based". Elements ''a'' and ''b'' can be swapped or otherwise re-arranged by the algorithm only when the order between these elements has been established based on the outcomes of prior comparisons. This is the case when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon Triangulation
In computational geometry, polygon triangulation is the partition of a polygonal area (simple polygon) into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is . Triangulations may be viewed as special cases of planar straight-line graphs. When there are no holes or added points, triangulations form maximal outerplanar graphs. Polygon triangulation without extra vertices Over time, a number of algorithms have been proposed to triangulate a polygon. Special cases It is trivial to triangulate any convex polygon in linear time into a fan triangulation, by adding diagonals from one vertex to all other non-nearest neighbor vertices. The total number of ways to triangulate a convex ''n''-gon by non-intersecting diagonals is the (''n''−2)nd Catalan number, which equals :\frac, a formula found by Leonhard Euler. A monotone polygon can be triangulated in linear time with either the algorithm of A. Fournier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raimund Seidel
Raimund G. Seidel is a German and Austrian theoretical computer scientist and an expert in computational geometry. Seidel was born in Graz, Austria, and studied with Hermann Maurer at the Graz University of Technology. He earned his M.Sc. in 1981 from University of British Columbia under David G. Kirkpatrick. He received his Ph.D. in 1987 from Cornell University under the supervision of John Gilbert. After teaching at the University of California, Berkeley, he moved in 1994 to Saarland University. In 1997, he and Christoph M. Hoffmann were program chairs for the Symposium on Computational Geometry. In 2014, he took over as Scientific Director of the Leibniz Center for Informatics (LZI) from Reinhard Wilhelm. Seidel invented backwards analysis of randomized algorithms and used it to analyze a simple linear programming algorithm that runs in linear time for problems of bounded dimension. With his student Cecilia R. Aragon in 1989 he devised the treap data structure, . an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Search
In computer science, linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched. A linear search runs in linear time in the worst case, and makes at most comparisons, where is the length of the list. If each element is equally likely to be searched, then linear search has an average case of comparisons, but the average case can be affected if the search probabilities for each element vary. Linear search is rarely practical because other search algorithms and schemes, such as the binary search algorithm and hash tables, allow significantly faster searching for all but short lists. Algorithm A linear search sequentially checks each element of the list until it finds an element that matches the target value. If the algorithm reaches the end of the list, the search terminates unsuccessfully. Basic algorithm Given a list of elements with values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kadane's Algorithm
In computer science, the maximum sum subarray problem, also known as the maximum segment sum problem, is the task of finding a contiguous subarray with the largest sum, within a given one-dimensional array data structure, array A[1...n] of numbers. It can be solved in O(n) time and O(1) space. Formally, the task is to find indices i and j with 1 \leq i \leq j \leq n , such that the sum : \sum_^j A[x] is as large as possible. (Some formulations of the problem also allow the empty subarray to be considered; by convention, empty sum, the sum of all values of the empty subarray is zero.) Each number in the input array A could be positive, negative, or zero. For example, for the array of values [−2, 1, −3, 4, −1, 2, 1, −5, 4], the contiguous subarray with the largest sum is [4, −1, 2, 1], with sum 6. Some properties of this problem are: # If the array contains all non-negative numbers, then the problem is trivial; a maximum subarray is the entire arra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-d Tree
In computer science, a ''k''-d tree (short for ''k-dimensional tree'') is a space-partitioning data structure for organizing points in a ''k''-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. ''k''-d trees are a useful data structure for several applications, such as: * Searches involving a multidimensional search key (e.g. range searches and nearest neighbor searches) & * Creating point clouds. ''k''-d trees are a special case of binary space partitioning trees. Description The ''k''-d tree is a binary tree in which ''every'' node is a ''k''-dimensional point. Every non-leaf node can be thought of as implicitly generating a splitting hyperplane that divides the space into two parts, known as half-spaces. Points to the left of this hyperplane are represented by the left subtree of that node and points to the right of the hyperplane are represented by the right subtree. The hyperplane direction is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Range Searching
In computer science, the range searching problem consists of processing a set ''S'' of objects, in order to determine which objects from ''S'' intersect with a query object, called the ''range''. For example, if ''S'' is a set of points corresponding to the coordinates of several cities, find the subset of cities within a given range of latitudes and longitudes. The range searching problem and the data structures that solve it are a fundamental topic of computational geometry. Applications of the problem arise in areas such as Geographic information system, geographical information systems (GIS), computer-aided design (CAD) and databases. Variations There are several variations of the problem, and different data structures may be necessary for different variations. In order to obtain an efficient solution, several aspects of the problem need to be specified: * Object types: Algorithms depend on whether ''S'' consists of Point (geometry), points, line (geometry), lines, line seg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |