|
Quadratic Set
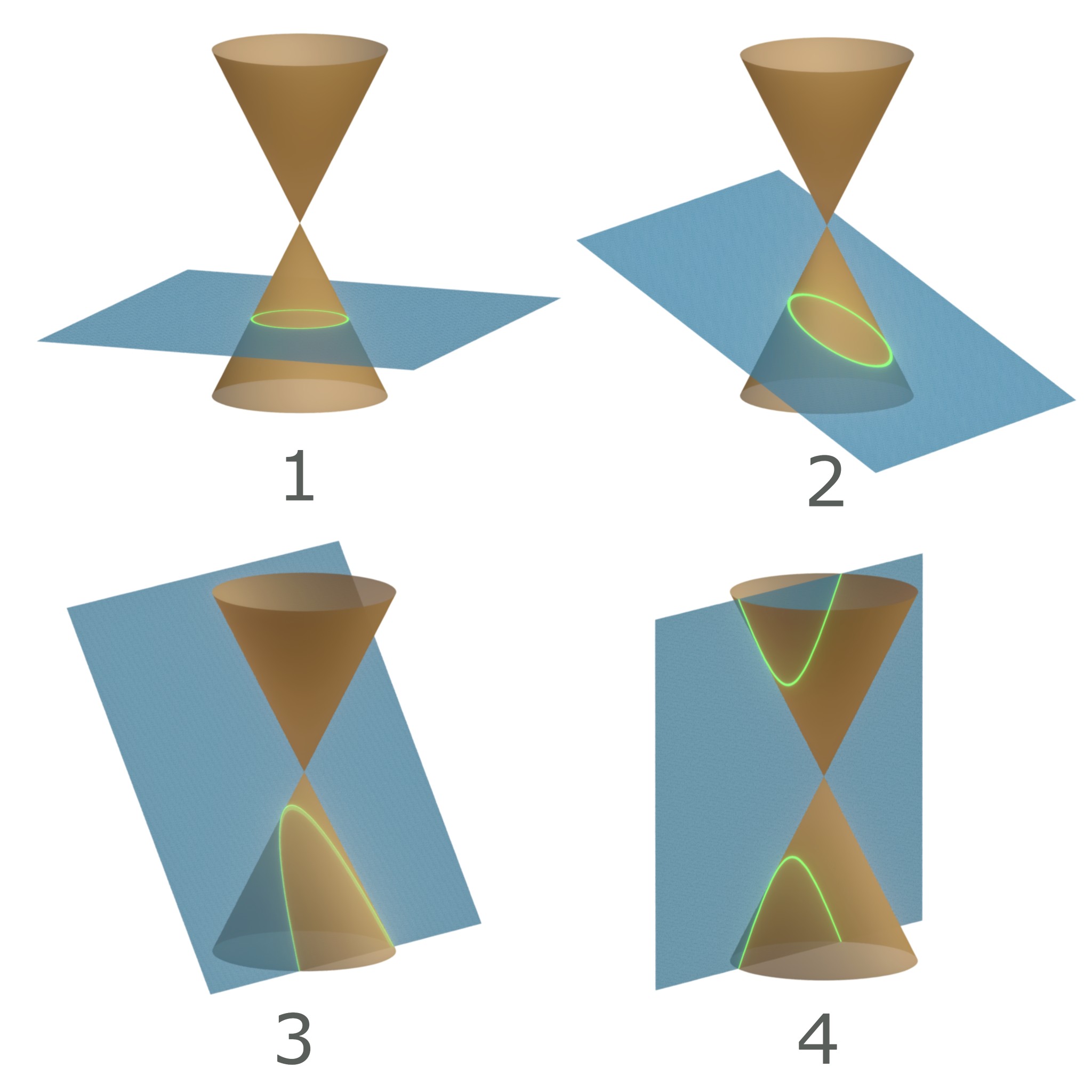
In mathematics, a quadratic set is a set of points in a projective space that bears the same essential incidence properties as a quadric (conic section in a projective plane, sphere or cone or hyperboloid in a projective space). Definition of a quadratic set Let \mathfrak P=(,,\in) be a projective space. A quadratic set is a non-empty subset of for which the following two conditions hold: :(QS1) Every line g of intersects in at most two points or is contained in . ::(g is called exterior to if , g\cap , =0, tangent to if either , g\cap , =1 or g\cap =g, and secant to if , g\cap , =2.) :(QS2) For any point P\in the union _P of all tangent lines through P is a hyperplane or the entire space . A quadratic set is called non-degenerate if for every point P\in , the set _P is a hyperplane. A Pappian projective space is a projective space in which Pappus's hexagon theorem holds. The following result, due to Francis Buekenhout, is an astonishing statement for finite projective ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the fol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone
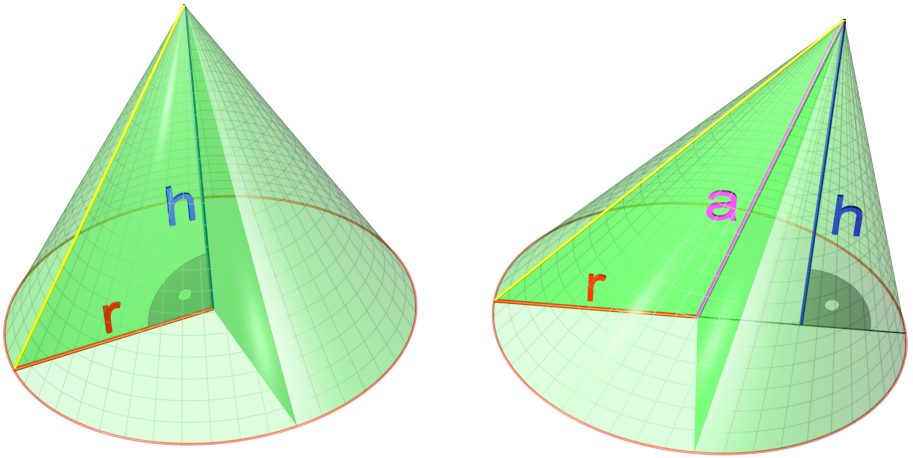
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperboloid
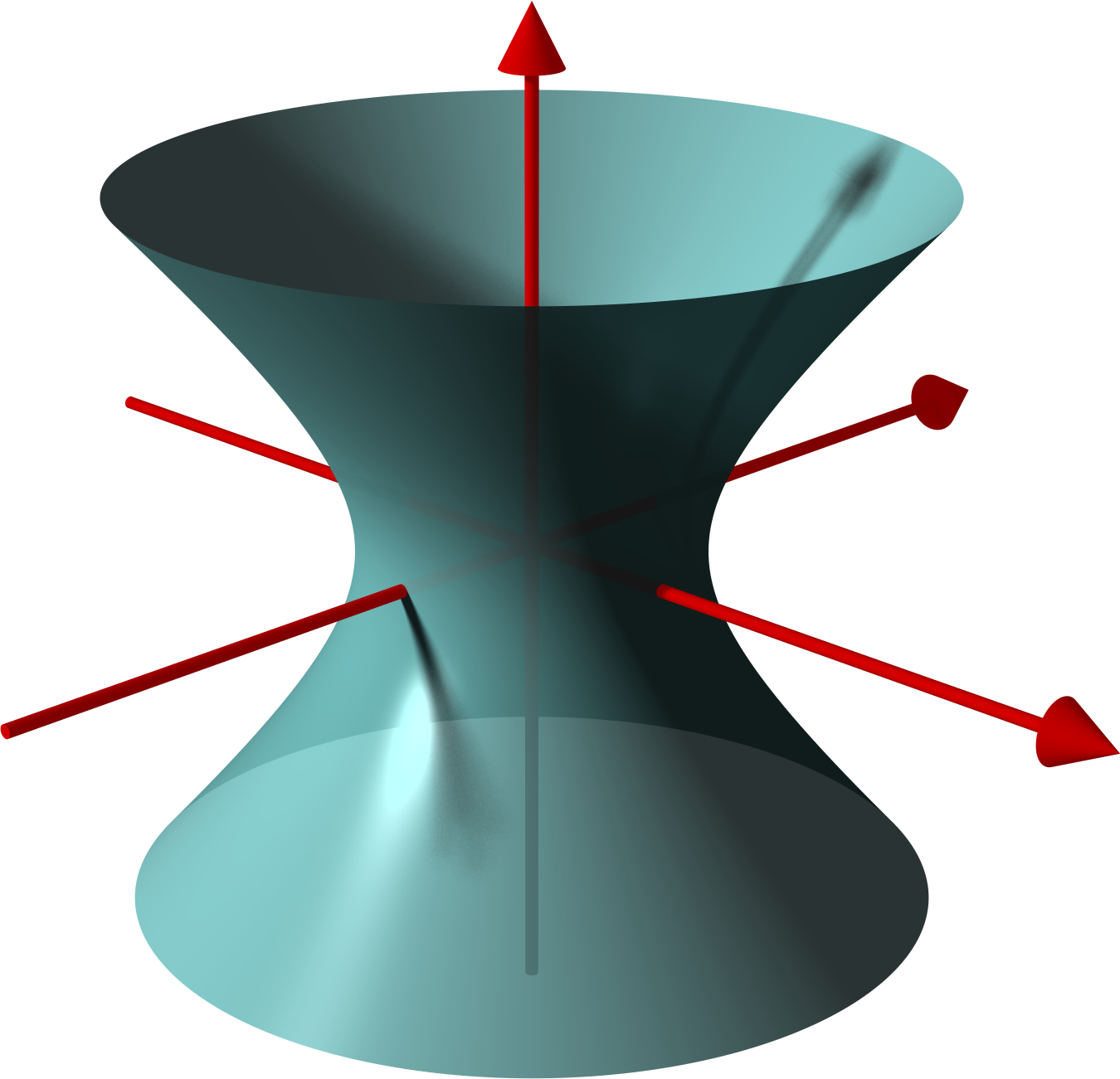
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and the ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined. In different settings, hyperplanes may have different properties. For instance, a hyperplane of an -dimensional affine space is a flat subset with dimension and it separates the space into two half spaces. While a hyperplane of an -dimensional projective space does not have this property. The difference in dimension between a subspace and its ambient space is known as the codimension of with respect to . Therefore, a necessary and sufficient condition for to be a hyperplane in is for to have codimension one in . Technical description In geometry, a hyperplane of an ''n''-dimensi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pappus's Hexagon Theorem
In mathematics, Pappus's hexagon theorem (attributed to Pappus of Alexandria) states that *given one set of collinear points A, B, C, and another set of collinear points a,b,c, then the intersection points X,Y,Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear, lying on the ''Pappus line''. These three points are the points of intersection of the "opposite" sides of the hexagon AbCaBc. It holds in a projective plane over any field, but fails for projective planes over any noncommutative division ring. Projective planes in which the "theorem" is valid are called pappian planes. If one restricts the projective plane such that the Pappus line u is the line at infinity, one gets the ''affine version'' of Pappus's theorem shown in the second diagram. If the Pappus line u and the lines g,h have a point in common, one gets the so-called little version of Pappus's theorem. The dual of this incidence theorem states that given one set of concurrent lines A, B, C, and an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Francis Buekenhout
Francis Buekenhout (born 23 April 1937 in Ixelles near Brussels) is a Belgian mathematician who introduced Buekenhout geometries and the concept of quadratic sets. Career Buekenhout studied at the University of Brussels under Jacques Tits and Paul Libois. Together with his teacher Jacques Tits, he developed concepts with the diagram geometries, also called Buekenhout geometries or Buekenhout–Tits geometries. These largely disregard the concrete axiom systems of a projective or affine geometry and put these and many other incidence geometries into a common framework. He worked at the ULB from 1960 to 1969 as an assistant to Libois. He was then appointed as extraordinary professor 1969 to 1998, and as ordinary professor from 1977 until his retirement in 2002. He has been a member of the Académie Royale des Sciences The French Academy of Sciences (French: ''Académie des sciences'') is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadric
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections (ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension ''D'') in a -dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in ''D'' + 1 variables; for example, in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a ''degenerate quadric'' or a ''reducible quadric''. In coordinates , the general quadric is thus defined by the algebraic equationSilvio LevQuadricsin "Geometry Formulas and Facts", excerpted from 30th Edition of ''CRC Standard Mathematical Tables and Formulas'', CRC Press, from The Geometry Center at University of Minnesota : \sum_^ x_i Q_ x_j + \sum_^ P_i x_i + R = 0 which may be compactly written in vector and matrix notation as: : x Q x^\mathrm + P x^\mathrm + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beniamino Segre
Beniamino Segre (16 February 1903 – 2 October 1977) was an Italian mathematician who is remembered today as a major contributor to algebraic geometry and one of the founders of finite geometry. Life and career He was born and studied in Turin. Corrado Segre, his uncle, also served as his doctoral advisor. Among his main contributions to algebraic geometry are studies of birational invariants of algebraic varieties, singularities and algebraic surfaces. His work was in the style of the old Italian School, although he also appreciated the greater rigour of modern algebraic geometry. Segre was a pioneer in finite geometry, in particular projective geometry based on vector spaces over a finite field. In a well-known paper he proved the following theorem: In a Desarguesian plane of odd order, the ovals are exactly the irreducible conics. In 1959 he authored a survey "Le geometrie di Galois" on Galois geometry. According to J. W. P. Hirschfeld, it "gave a comprehensive list of r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field (algebra)
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics. The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and ''p''-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many elements. The relation of two fields is expressed by the notion of a field extension. Galois theory, initiated by Évariste Galois in the 1830s, is devoted to understanding the symmetries of field extensions. Among other results, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Albrecht Beutelspacher
Albrecht Beutelspacher (born 5 June 1950) is a German mathematician and founder of the Mathematikum. He is a professor emeritus of the University of Giessen, where he held the chair for geometry and discrete mathematics from 1988 to 2018. Biography Beutelspacher studied 1969-1973 math, physics and philosophy at the University of Tübingen and received his PhD 1976 from the University of Mainz. His PhD advisor was Judita Cofman. From 1982-1985 he was an associate professor at the University of Mainz and from 1985-1988 he worked for a research department of the Siemens. From 1988 to 2018 he was a tenured professor for geometry and discrete mathematics at the University of Giessen. He became a well-known popularizer of mathematics in Germany by authoring several books in the field of popular science and recreational math and by founding Germany's first math museum, the Mathematikum. He received several awards for his contributions to popularizing mathematics. He has a math column ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |