|
Quadratic Cone
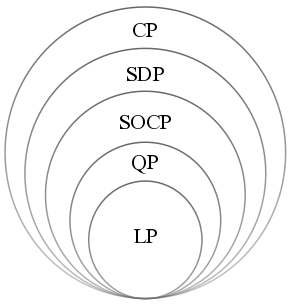
A second-order cone program (SOCP) is a convex optimization problem of the form :minimize \ f^T x \ :subject to ::\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i,\quad i = 1,\dots,m ::Fx = g \ where the problem parameters are f \in \mathbb^n, \ A_i \in \mathbb^, \ b_i \in \mathbb^, \ c_i \in \mathbb^n, \ d_i \in \mathbb, \ F \in \mathbb^, and g \in \mathbb^p. x\in\mathbb^n is the optimization variable. \lVert x \rVert_2 is the Euclidean norm and ^T indicates transpose. The "second-order cone" in SOCP arises from the constraints, which are equivalent to requiring the affine function (A x + b, c^T x + d) to lie in the second-order cone in \mathbb^. SOCPs can be solved by interior point methods and in general, can be solved more efficiently than semidefinite programming (SDP) problems. Some engineering applications of SOCP include filter design, antenna array weight design, truss design, and grasping force optimization in robotics. Applications in quantitative finance include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Definition Abstract form A convex optimization problem is defined by two ingredients: * The ''objective function'', which is a real-valued convex function of ''n'' variables, f :\mathcal D \subseteq \mathbb^n \to \mathbb; * The ''feasible set'', which is a convex subset C\subseteq \mathbb^n. The goal of the problem is to find some \mathbf \in C attaining :\inf \. In general, there are three options regarding the existence of a solution: * If such a point ''x''* exists, it is referred to as an ''optimal point'' or ''solution''; the set of all optimal points is called the ''optimal set''; and the problem is called ''solvable''. * If f is unbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semialgebraic Set
In mathematics, a basic semialgebraic set is a set defined by polynomial equalities and polynomial inequalities, and a semialgebraic set is a finite union of basic semialgebraic sets. A semialgebraic function is a function with a semialgebraic graph. Such sets and functions are mainly studied in real algebraic geometry which is the appropriate framework for algebraic geometry over the real numbers. Definition Let \mathbb be a real closed field (For example \mathbb could be the field of real numbers \mathbb). A subset S of \mathbb^n is a ''semialgebraic set'' if it is a finite union of sets defined by polynomial equalities of the form \ and of sets defined by polynomial inequalities of the form \. Properties Similarly to algebraic subvarieties, finite unions and intersections of semialgebraic sets are still semialgebraic sets. Furthermore, unlike subvarieties, the complement of a semialgebraic set is again semialgebraic. Finally, and most importantly, the Tarski–Seide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Cone
In linear algebra, a power cone is a kind of a convex cone that is particularly important in modeling convex optimization problems. It is a generalization of the quadratic cone: the quadratic cone is defined using a quadratic equation (with the power 2), whereas a power cone can be defined using any power, not necessarily 2. Definition The ''n''-dimensional power cone is parameterized by a real number 0 Applications The main application of the power cone is in constraints ofconvex optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex ...
[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NAG Numerical Library
The NAG Numerical Library is a commercial software product developed and sold by The Numerical Algorithms Group Ltd. It is a software library of numerical-analysis routines, containing more than 1,900 mathematical and statistical algorithms. Areas covered by the library include linear algebra, optimization, quadrature, the solution of ordinary and partial differential equations, regression analysis, and time series analysis. Users of the NAG Library call its routines from within their applications to incorporate its mathematical or statistical functionality and to solve numerical problems - for example, finding the minimum or maximum of a function, fitting a curve or surface to data, or solving a differential equation. The NAG Library can be accessed from a variety of programming languages and environments such as C/ C++, Fortran,Python, Active Directory (AD), MATLAB, Java, and .NET. The main supported systems are currently Windows, Linux and macOS running on x86-64 arch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MOSEK
MOSEK is a software package for the solution of linear, mixed-integer linear, quadratic, mixed-integer quadratic, quadratically constrained, conic and convex nonlinear mathematical optimization problems. The applicability of the solver varies widely and is commonly used for solving problems in areas such as engineering, finance and computer science. The emphasis in MOSEK is on solving large-scale sparse problems linear and conic optimization problems. In particular, MOSEK solves conic quadratic (a.k.a. Second-order cone programming) and semi-definite (aka. semidefinite programming) problems. A special feature of the solver, is its interior-point optimizer, based on the so-called homogeneous model. This implies that MOSEK can reliably detect a primal and/or dual infeasible status as documented in several published papers. In addition to the interior-point optimizer MOSEK includes: * Primal and dual simplex optimizer for linear problems. * Mixed-integer optimizer for linear, quad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. , MATLAB has more than four million users worldwide. They come from various backgrounds of engineering, science, and economics. , more than 5000 global colleges and universities use MATLAB to support instruction and research. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gurobi Optimizer
Gurobi Optimizer is a prescriptive analytics platform and a decision-making technology developed by Gurobi Optimization, LLC. The Gurobi Optimizer (often referred to as simply, “Gurobi”) is a solver, since it uses mathematical optimization to calculate the answer to a problem. Gurobi is included in the Q1 2022 inside BIGDATA “Impact 50 List” as an honorable mention. History Dr. Zonghao Gu, Dr. Edward Rothberg, and Dr. Robert Bixby founded Gurobi in 2008, coming up with the name by combining the first two letters of their last names. Gurobi is used for linear programming (LP), quadratic programming (QP), quadratically constrained programming (QCP), mixed integer linear programming (MILP), mixed-integer quadratic programming (MIQP), and mixed-integer quadratically constrained programming (MIQCP). In 2016, Dr. Bistra Dilkina from Georgia Tech discussed how she uses Gurobi in the field of computational sustainability, to optimize movement corridors for wildlife, inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FICO Xpress
The FICO Xpress optimizer is a commercial optimization solver for linear programming (LP), mixed integer linear programming (MILP), convex quadratic programming (QP), convex quadratically constrained quadratic programming (QCQP), second-order cone programming (SOCP) and their mixed integer counterparts. Xpress includes a general purpose nonlinear global solver, Xpress Global, and a nonlinear local solver, Xpress NonLinear, including a successive linear programming algorithm (SLP, first-order method), and Artelys Knitro (second-order methods). Xpress was originally developed by Dash Optimization, and was acquired by FICO in 2008. Its initial authors were Bob Daniel and Robert Ashford. The first version of Xpress could only solve LPs; support for MIPs was added in 1986. Being released in 1983, Xpress was the first commercial LP and MIP solver running on PCs. In 1992, an Xpress version for parallel computing was published, which was extended to distributed computing five years late ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CPLEX
IBM ILOG CPLEX Optimization Studio (often informally referred to simply as CPLEX) is an optimization software package. History The CPLEX Optimizer was named after the simplex method implemented in the C programming language. However, today it also supports other types of mathematical optimization and offers interfaces other than C. It was originally developed by Robert E. Bixby and sold commercially in 1988 by CPLEX Optimization Inc. This was acquired by ILOG in 1997 and ILOG was subsequently acquired by IBM in January 2009. CPLEX continues to be actively developed by IBM. Features The IBM ILOG CPLEX Optimizer solves integer programming problems, very large linear programming problems using either primal or dual variants of the simplex method or the barrier interior point method, convex and non-convex quadratic programming problems, and convex quadratically constrained problems (solved via second-order cone programming, or SOCP). The CPLEX Optimizer has a modelin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artelys Knitro
Artelys Knitro is a commercial software package for solving large scale nonlinear mathematical optimization problems. KNITRO – (the original solver name) short for "Nonlinear Interior point Trust Region Optimization" (the "K" is silent) – was co-created by Richard Waltz, Jorge Nocedal, Todd Plantenga and Rich Byrd. It was first introduced in 2001, as a derivative of academic research at Northwestern University. Subsequently, it was developed by Ziena Optimization LLC, which has been bought by Frech Artelys. Optimization problems must be presented to Knitro in mathematical form, and should provide a way of computing function derivatives using sparse matrices (Knitro can compute derivatives approximation but in most cases providing the exact derivatives is beneficial). An often easier approach is to develop the optimization problem in an algebraic modeling language. The modeling environment computes function derivatives, and Knitro is called as a "solver" from within the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
AMPL
AMPL (A Mathematical Programming Language) is an algebraic modeling language to describe and solve high-complexity problems for large-scale mathematical computing (e.g. large-scale optimization and scheduling-type problems). It was developed by Robert Fourer, David Gay, and Brian Kernighan at Bell Laboratories. AMPL supports dozens of solvers, both open source and commercial software, including CBC, CPLEX, FortMP, MOSEK, MINOS, IPOPT, SNOPT, KNITRO, and LGO. Problems are passed to solvers as nl files. AMPL is used by more than 100 corporate clients, and by government agencies and academic institutions. One advantage of AMPL is the similarity of its syntax to the mathematical notation of optimization problems. This allows for a very concise and readable definition of problems in the domain of optimization. Many modern solvers available on the NEOS Server (formerly hosted at the Argonne National Laboratory, currently hosted at the University of Wisconsin, Madison) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ALGLIB
ALGLIB is a cross-platform open source numerical analysis and data processing library. It can be used from several programming languages ( C++, C#, VB.NET, Python, Delphi, Java). ALGLIB started in 1999 and has a long history of steady development with roughly 1-3 releases per year. It is used by several open-source projects, commercial libraries, and applications (e.g. TOL project, Math.NET Numerics, SpaceClaim). Features Distinctive features of the library are: * Support for several programming languages with identical APIs (as of 2023, it supports C++, C#, FreePascal/Delphi, VB.NET, Python, and Java) * Self-contained code with no mandatory external dependencies and easy installation * Portability (it was tested under x86/x86-64/ARM, Windows and Linux) * Two independent backends (pure C# implementation, native C implementation) with automatically generated APIs (C++, C#, ...) * Same functionality of commercial and GPL versions, with enhancements for speed and parallelism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |