|
Petr Vaníček
Petr Vaníček (born 18 July 1935) is a Czech Canadian geodesist and theoretical geophysicist who has made important breakthroughs in theory of spectral analysis and geoid computation. Main contributions Research One of Vaníček's main contributions of general relevance is least-squares spectral analysis, also called the Vaníček method, a frequency spectrum computation method published in 1969 and 1971. The method is based on a least-squares fit of sinusoids to the data samples, and mitigates the drawbacks of applying Fourier analysis for analyzing long incomplete data records such as most natural datasets. Unlike with Fourier analysis, data need not be equally spaced to use Vaníček analysis. His discoveries in theoretical geophysics, the "precise geoid solution" in particular, enable millimetre-to-centimetre accuracy in geoid computation, an-order-of-magnitude improvement from previous solutions. Service Vaníček initiated the establishing of the Canadian Geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sušice
Sušice (; german: Schüttenhofen) is a town in Klatovy District in the Plzeň Region of the Czech Republic. It has about 11,000 inhabitants. The historic town centre is well preserved and is protected by law as an urban monument zone. Administrative parts Sušice is made up of 17 town parts and villages: Sušice I–III, Albrechtice, Červené Dvorce, Chmelná, Divišov, Dolní Staňkov, Humpolec, Milčice, Nuzerov, Páteček, Rok, Stráž, Volšovy, Vrabcov and Záluží. Etymology The name Sušice is derived from the Czech verb ''sušit'', i.e. "dry". At the time of its establishment, it was a place where gold panners dried the gold sand after washing. Geography Sušice is located about southeast of Klatovy and south of Plzeň. It lies in the Bohemian Forest Foothills. The highest point is the hill Sedlo at above sea level. The Otava River flows through the town. Climate Average daily temperature in July is about , while January mean temperatures are typically . The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
USACE
, colors = , anniversaries = 16 June (Organization Day) , battles = , battles_label = Wars , website = , commander1 = LTG Scott A. Spellmon , commander1_label = Chief of Engineers and Commanding General of the U.S. Army Corps of Engineers , commander2 = MGbr>Richard J. Heitkamp, commander2_label = Deputy Chief of Engineers and Deputy Commanding General , commander3 = MGKimberly M. Colloton, commander3_label = Deputy Commanding General for Military and International Operations , commander4 = MGbr>William H. Graham, commander4_label = Deputy Commanding General for Civil and Emergency Operations , commander5 = COLbr>James J. Handura, commander5_label = Chief of Staff for the U.S. Army Corps of Engin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', '' ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', '' angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least-squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. The most important application is in data fitting. When the problem has substantial uncertainties in the independent variable (the ''x'' variable), then simple regression and least-squares methods have problems; in such cases, the methodology required for fitting errors-in-variables models may be considered instead of that for least squares. Least squares problems fall into two categories: linear or ordinary least squares and nonlinear least squares, depending on whether or not the residuals are linear in all unknowns. The linear least-squares problem occurs in statistical regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least-squares Spectral Analysis
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems. Unlike with Fourier analysis, data need not be equally spaced to use LSSA. LSSA is also known as the Vaníček method or the Gauss-Vaniček method after Petr Vaníček, and as the Lomb method or the Lomb–Scargle periodogram, based on the contributions of Nicholas R. Lomb and, independently, Jeffrey D. Scargle. Historical background The close connections between Fourier analysis, the periodogram, and least-squares fitting of sinusoids have long been known. Most developments, however, are restricted to complete data sets of equally spaced samples. In 1963, Freek J. M. Barning of Mathematisch Centrum, Amsterdam, handled unequally spaced data by similar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
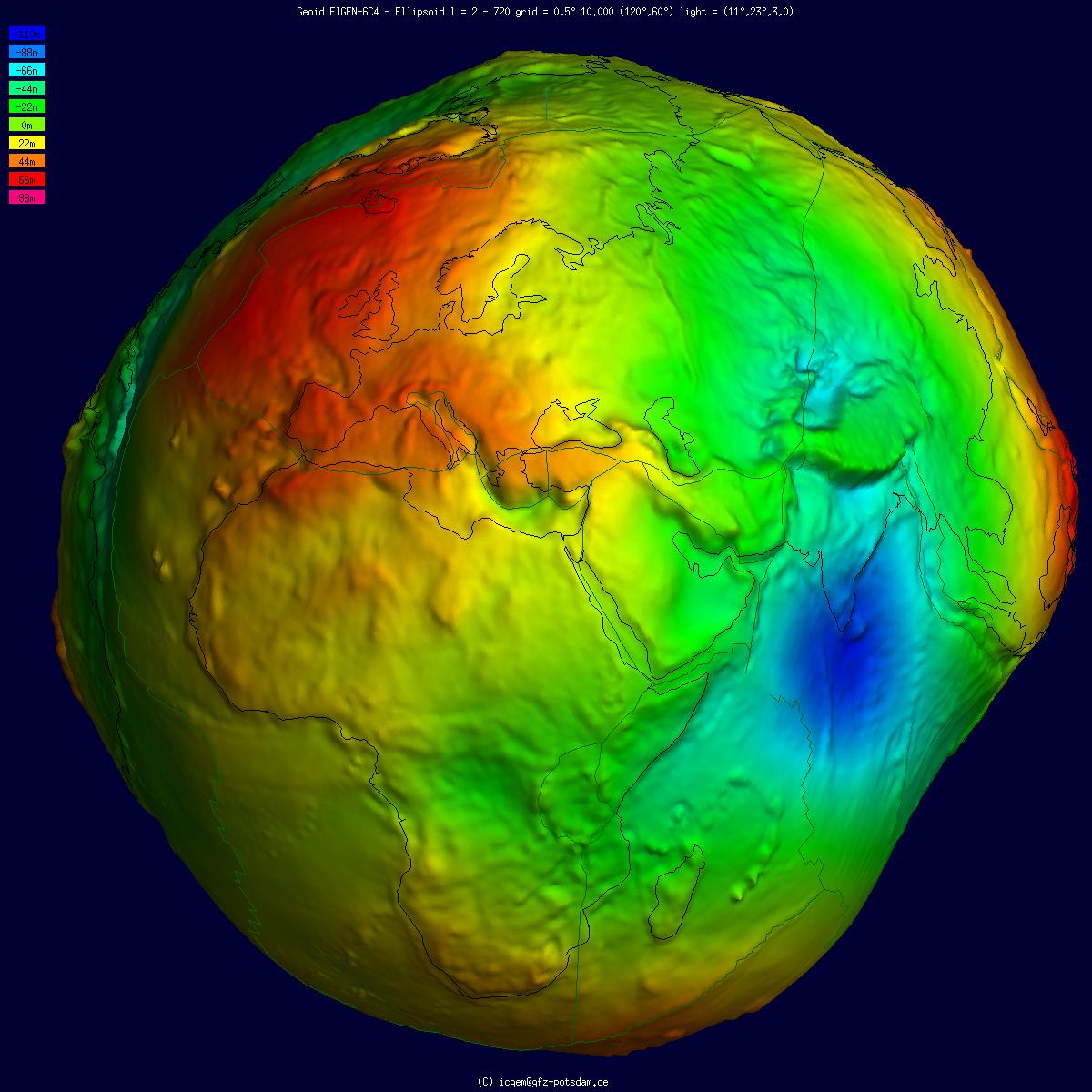
Geoid
The geoid () is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as with very narrow hypothetical canals). According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century. All points on a geoid surface have the same geopotential (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Spectrum
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Geophysicists
This is a list of geophysicists, people who made notable contributions to geophysics, whether or not geophysics was their primary field. These include historical figures who laid the foundations for the field of geophysics. More recently, some of the top awards for geophysicists are the Vetlesen Prize (intended to be the equivalent of a Nobel Prize for geology or geophysics); the William Bowie Medal (the top award of the American Geophysical Union); the Maurice Ewing Medal (the top award of the Society of Exploration Geophysicists); and the Crafoord Prize for geosciences. Some geophysicists have also won more general prizes such as the Nobel Prize and the Kyoto Prize. A * Leason Adams (American, 1887–1969) – high pressure mineral physics * Thomas J Ahrens (American, 1936–2010) – experimental methods for modeling hypervelocity impacts and materials in the Earth's core and mantle * Hannes Alfvén (Swedish, 1908–1995) – Alfvén waves, magnetohydrodynamics of magnetosp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesist
Geodesy ( ) is the Earth science of accurately measuring and understanding Earth's figure (geometric shape and size), orientation in space, and gravity. The field also incorporates studies of how these properties change over time and equivalent measurements for other planets (known as ''planetary geodesy''). Geodynamical phenomena, including crustal motion, tides and polar motion, can be studied by designing global and national control networks, applying space geodesy and terrestrial geodetic techniques and relying on datums and coordinate systems. The job title is geodesist or geodetic surveyor. History Definition The word geodesy comes from the Ancient Greek word ''geodaisia'' (literally, "division of Earth"). It is primarily concerned with positioning within the temporally varying gravitational field. Geodesy in the German-speaking world is divided into "higher geodesy" ( or ), which is concerned with measuring Earth on the global scale, and "practical geodesy" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Czech Canadian
Czech Canadians are Canadian citizens of Czech ancestry or Czech-born people who reside in Canada. They were frequently called Bohemian Canadians until the late 19th century. According to the 2006 Canadian census, there were 98,090 Canadians of full or partial Czech descent. Number of Czech and Czechoslovak Canadians Data from this section from Statistics Canada, 2016. Notable people * Karla Homolka - serial killer * Vasek Pospisil - tennis player * Jenna Talackova - model, TV personality * Otto Jelinek - businessman, former figure skater, politician * Thomas J. Bata - businessman, "Shoemaker to the World" * Josef Škvorecký - writer, publisher * Ivan Reitman - director * David Nykl - actor * Vaclav Smil - scientist and policy analyst * Karina Gould - politician See also * Demographics of the Czech Republic * Canada–Czech Republic relations * Czech people * European Canadians Further reading *Encyclopedia of Canada's Peoples"Czechs:Origins." Multicultural Canada. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canadian Geophysical Union
The Canadian Geophysical Union (French: Union géophysique canadienne) (CGU) began as a society dedicated to the scientific study of the solid earth and has evolved into one that is concerned with all aspects of the physical study of Earth and its space environment, including the Sun and solar system. To express this broader vision of the geophysical sciences, the Union has adopted a sectional structure that allows individual sections to function as semi-autonomous entities. Goals * Advance and promote the scientific study of Earth and its environment in space and to serve as a national focus for the geophysical sciences in Canada. * Foster cooperation between the Canadian geophysical community and other national and international scientific organizations. * Encourage communication through the organization and sponsorship of conferences and the publication of scientific results. * Promote integration of geophysical knowledge with that of other sciences concerned with the improvement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)