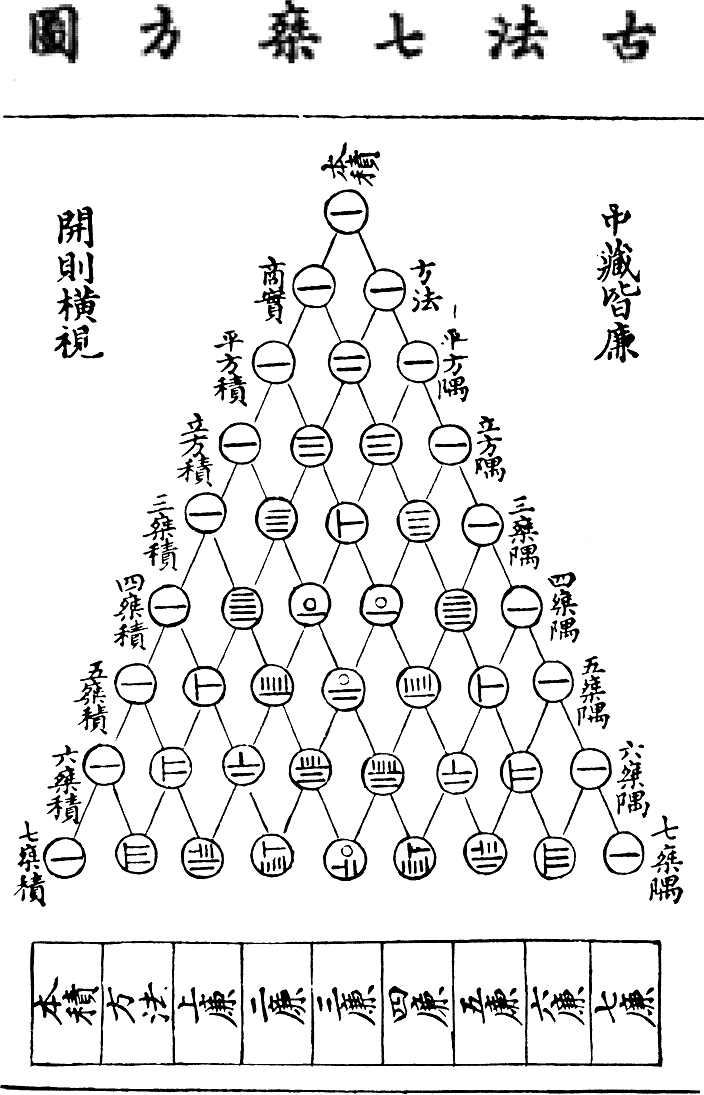
|
Pascal's Triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy. The rows of Pascal's triangle are conventionally enumerated starting with row n = 0 at the top (the 0th row). The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mount Meru
Mount Meru (Sanskrit/Pali: मेरु), also known as Sumeru, Sineru or Mahāmeru, is the sacred five-peaked mountain of Hindu, Jain, and Buddhist cosmology and is considered to be the centre of all the physical, metaphysical and spiritual universes. There is no clear identification of Mount Meru with a particular geophysical location. Many famous Buddhist, Jain, and Hindu temples have been built as symbolic representations of this mountain. The "Sumeru Throne" 須彌座 xūmízuò style base is a common feature of Chinese pagodas. The highest point (the finial bud) on the pyatthat, a Burmese-style multi-tiered roof, represents Mount Meru. Etymology Etymologically, the proper name of the mountain is Meru (Sanskrit: Meru), to which is added the approbatory prefix su-, resulting in the meaning "excellent Meru" or "wonderful Meru". ''Meru'' is also the name of the central bead in a mālā. In other languages In other languages, Mount Meru is pronounced: * Assamese: � ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gersonides
Levi ben Gershon (1288 – 20 April 1344), better known by his Graecized name as Gersonides, or by his Latinized name Magister Leo Hebraeus, or in Hebrew by the abbreviation of first letters as ''RaLBaG'', was a medieval French Jewish philosopher, Talmudist, mathematician, physician and astronomer/astrologer. He was born at Bagnols in Languedoc, France. According to Abraham Zacuto and others, he was the son of Gerson ben Solomon Catalan. Biography As in the case of the other medieval Jewish philosophers little is known of his life. His family had been distinguished for piety and exegetical skill in Talmud, but though he was known in the Jewish community by commentaries on certain books of the Bible, he never seems to have accepted any rabbinical post. It has been suggested that the uniqueness of his opinions may have put obstacles in the way of his advancement to a higher position or office. He is known to have been at Avignon and Orange during his life, and is believed to have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordanus De Nemore
Jordanus de Nemore (fl. 13th century), also known as Jordanus Nemorarius and Giordano of Nemi, was a thirteenth-century European mathematician and scientist. The literal translation of Jordanus de Nemore (Giordano of Nemi) would indicate that he was an Italian. Bertrand Gille, ''Les ingénieurs de la Renaissance''. He wrote treatises on at least 6 different important mathematical subjects: the science of weights; “algorismi” treatises on practical arithmetic; pure arithmetic; algebra; geometry; and stereographic projection. Most of these treatises exist in several versions or reworkings from the Middle Ages. We know nothing about him personally, other than the approximate date of his work. Life No biographical details are known about Jordanus de Nemore. Cited in the early manuscripts simply as “Jordanus”, he was later given the sobriquet of “de Nemore” (“of the Forest,” “Forester”) which does not add any firm biographical information. In the Renaissance his na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yang Hui
Yang Hui (, ca. 1238–1298), courtesy name Qianguang (), was a Chinese mathematician and writer during the Song dynasty. Originally, from Qiantang (modern Hangzhou, Zhejiang), Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting Yang Hui's Triangle. This triangle was the same as Pascal's Triangle, discovered by Yang's predecessor Jia Xian. Yang was also a contemporary to the other famous mathematician Qin Jiushao. Written work The earliest extant Chinese illustration of 'Pascal's triangle' is from Yang's book ''Xiangjie Jiuzhang Suanfa'' ()Fragments of this book was retained in the Yongle Encyclopedia vol 16344, in British Museum Library of 1261 AD, in which Yang acknowledged that his method of finding square roots and cubic roots using "Yang Hui's Triangle" was invented by mathematician Jia XianNeedham, Volume 3, 134-137. who expounded it around 1100 AD, about 500 years before Pascal. In his book (now los ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jia Xian
Jia Xian (; ca. 1010–1070) was a Chinese mathematician from Kaifeng of the Song dynasty. Biography According to the history of the Song dynasty, Jia was a palace eunuch of the Left Duty Group. He studied under the mathematician Chu Yan, and was well versed in mathematics, writing many books on the subject. Jia Xian described the Pascal's triangle (Jia Xian triangle) around the middle of the 11th century, about six centuries before Pascal. Jia used it as a tool for extracting square and cubic roots. The original book by Jia entitled ''Shi Suo Suan Shu'' was lost; however, Jia's method was expounded in detail by Yang Hui, who explicitly acknowledged his source: "My method of finding square and cubic roots was based on the Jia Xian method in ''Shi Suo Suan Shu''." A page from the ''Yongle Encyclopedia The ''Yongle Encyclopedia'' () or ''Yongle Dadian'' () is a largely-lost Chinese ''leishu'' encyclopedia commissioned by the Yongle Emperor of the Ming dynasty in 1403 and compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The American Mathematical Monthly
''The American Mathematical Monthly'' is a mathematical journal founded by Benjamin Finkel in 1894. It is published ten times each year by Taylor & Francis for the Mathematical Association of America. The ''American Mathematical Monthly'' is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. In this the ''American Mathematical Monthly'' fulfills a different role from that of typical mathematical research journals. The ''American Mathematical Monthly'' is the most widely read mathematics journal in the world according to records on JSTOR. Tables of contents with article abstracts from 1997–2010 are availablonline The MAA gives the Lester R. Ford Awards annually to "authors of articles of expository excellence" published in the ''American Mathematical Monthly''. Editors *2022– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nth Root
In mathematics, a radicand, also known as an nth root, of a number ''x'' is a number ''r'' which, when raised to the power ''n'', yields ''x'': :r^n = x, where ''n'' is a positive integer, sometimes called the ''degree'' of the root. A root of degree 2 is called a ''square root'' and a root of degree 3, a ''cube root''. Roots of higher degree are referred by using ordinal numbers, as in ''fourth root'', ''twentieth root'', etc. The computation of an th root is a root extraction. For example, 3 is a square root of 9, since 3 = 9, and −3 is also a square root of 9, since (−3) = 9. Any non-zero number considered as a complex number has different complex th roots, including the real ones (at most two). The th root of 0 is zero for all positive integers , since . In particular, if is even and is a positive real number, one of its th roots is real and positive, one is negative, and the others (when ) are non-real complex numbers; if is even and is a negative real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the exponents and are nonnegative integers with , and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in the term of is known as the binomial coefficient \tbinom or \tbinom (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where \tbinom gives the number of different combinations of elements that can be chosen from an -element set. Therefore \tbinom is often pronounced as " choose ". History Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid ment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Omar Khayyám
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a polymath, known for his contributions to mathematics, astronomy, philosophy, and Persian poetry. He was born in Nishapur, the initial capital of the Seljuk Empire. As a scholar, he was contemporary with the rule of the Seljuk dynasty around the time of the First Crusade. As a mathematician, he is most notable for his work on the classification and solution of cubic equations, where he provided geometric solutions by the intersection of conics. Khayyam also contributed to the understanding of the parallel axiom.Struik, D. (1958). "Omar Khayyam, mathematician". ''The Mathematics Teacher'', 51(4), 280–285. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar, a solar calendar with a very precise 33-year intercalation cycle''The Cambr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Al-Karaji
( fa, ابو بکر محمد بن الحسن الکرجی; c. 953 – c. 1029) was a 10th-century Persian people, Persian mathematician and engineer who flourished at Baghdad. He was born in Karaj, a city near Tehran. His three principal surviving works are mathematical: ''Al-Badi' fi'l-hisab'' (''Wonderful on calculation''), ''Al-Fakhri fi'l-jabr wa'l-muqabala'' (''Glorious on algebra''), and ''Al-Kafi fi'l-hisab'' (''Sufficient on calculation''). Work Al-Karaji wrote on mathematics and engineering. Some consider him to be merely reworking the ideas of others (he was influenced by Diophantus) but most regard him as more original, in particular for the beginnings of freeing algebra from geometry. Among historians, his most widely studied work is his algebra book ''al-fakhri fi al-jabr wa al-muqabala'', which survives from the medieval era in at least four copies. In his book "Extraction of hidden waters" he has mentioned that earth is spherical in shape but considers it t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics In Medieval Islam
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius of Perga, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full development of the decimal place-value system to include decimal fractions, the first systematised study of algebra, and advances in geometry and trigonometry. Arabic works played an important role in the transmission of mathematics to Europe during the 10th—12th centuries. Concepts Algebra The study of algebra, the name of which is derived from the Arabic language, Arabic word meaning completion or "reunion of broken parts", flourished during the Islamic golden age. Muhammad ibn Musa al-Khwarizmi, a Persian scholar in the House of Wisdom in Baghdad was the founder of algebra, is along with the Greek people, Greek mathematician Diophantus, known as the father of algebra. In his book ''The Compendious Book on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |