|
Pulsatile
In fluid dynamics, a flow with periodic variations is known as pulsatile flow, or as Womersley flow. The flow profiles was first derived by John R. Womersley (1907–1958) in his work with blood flow in arteries. The cardiovascular system of chordate animals is a very good example where pulsatile flow is found, but pulsatile flow is also observed in engines and hydraulic systems, as a result of rotating mechanisms pumping the fluid. Equation The pulsatile flow profile is given in a straight pipe by : u(r, t) = \mathrm\left\ \, , where: : Properties Womersley number The pulsatile flow profile changes its shape depending on the Womersley number :\alpha = R \left( \frac \right)^ \,. For \alpha \lesssim 2, viscous forces dominate the flow, and the pulse is considered quasi-static with a parabolic profile. For \alpha \gtrsim 2, the inertial forces are dominant in the central core, whereas viscous forces dominate near the boundary layer. Thus, the velocity profile gets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
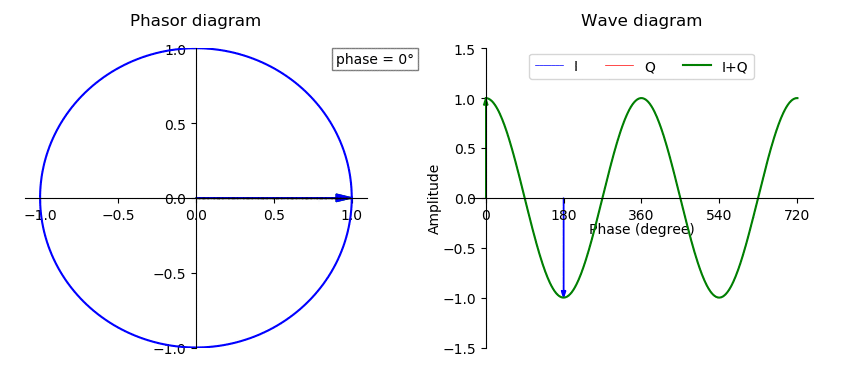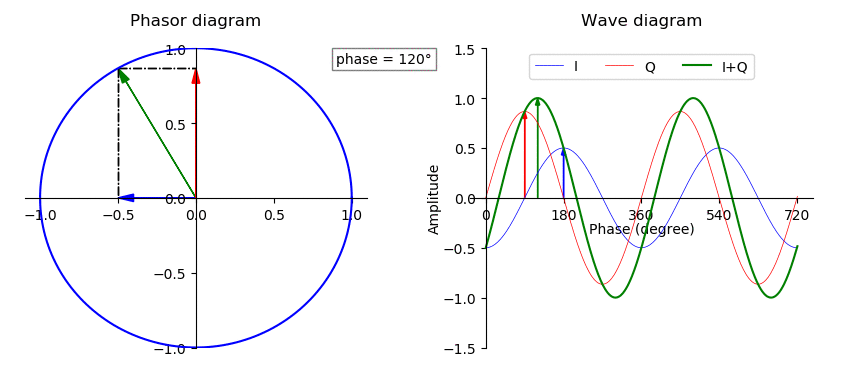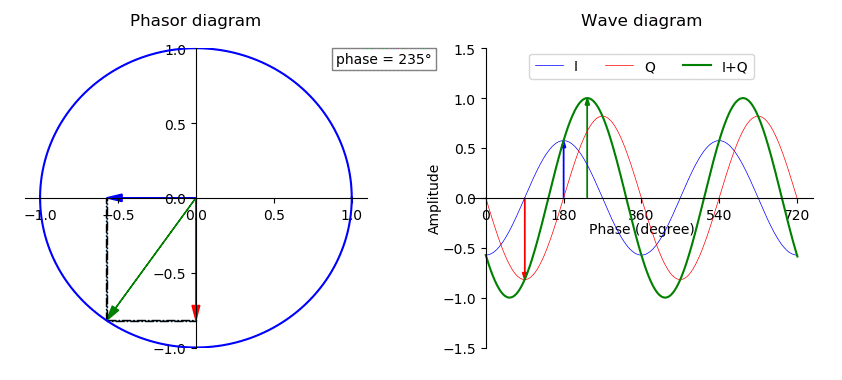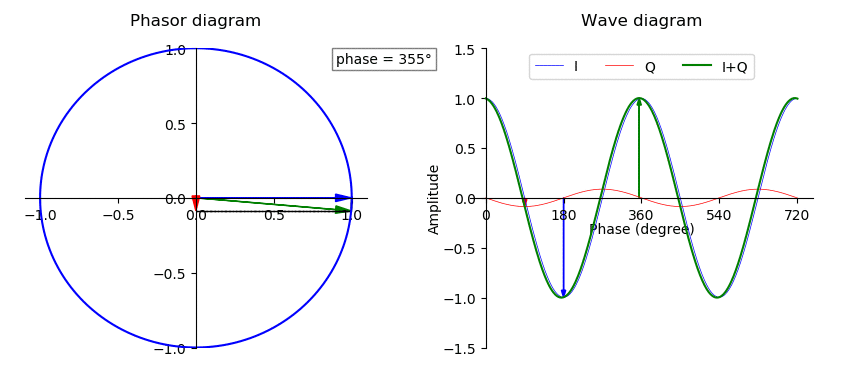
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasistatic Equilibrium
In thermodynamics, a quasi-static process, also known as a quasi-equilibrium process (from Latin ''quasi'', meaning ‘as if’), is a thermodynamic process that happens slowly enough for the system to remain in internal physical (but not necessarily chemical) thermodynamic equilibrium. An example of this is quasi-static expansion of a mixture of hydrogen and oxygen gas, where the volume of the system changes so slowly that the pressure remains uniform throughout the system at each instant of time during the process. Such an idealized process is a succession of physical equilibrium states, characterized by infinite slowness.Rajput, R.K. (2010). ''A Textbook of Engineering Thermodynamics'', 4th edition, Laxmi Publications (P) Ltd, New Delhi, pages 21, 45, 58. Only in a quasi-static thermodynamic process can we exactly define intensive quantities (such as pressure, temperature, specific volume, specific entropy) of the system at any instant during the whole process; otherwise, sin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Number
An imaginary number is the product of a real number and the imaginary unit , is usually used in engineering contexts where has other meanings (such as electrical current) which is defined by its property . The square (algebra), square of an imaginary number is . For example, is an imaginary number, and its square is . The number 0, zero is considered to be both real and imaginary. Originally coined in the 17th century by René Descartes as a derogatory term and regarded as fictitious or useless, the concept gained wide acceptance following the work of Leonhard Euler (in the 18th century) and Augustin-Louis Cauchy and Carl Friedrich Gauss (in the early 19th century). An imaginary number can be added to a real number to form a complex number of the form , where the real numbers and are called, respectively, the ''real part'' and the ''imaginary part'' of the complex number. History Although the Greek mathematician and engineer Heron of Alexandria is noted as the first t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, which represents the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when solving the Helmholtz equation in spherical coordinates. Applications Bessel's equation arises when finding separa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Viscosity
Viscosity is a measure of a fluid's rate-dependent resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for example, syrup has a higher viscosity than water. Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus its SI units are newton-seconds per metre squared, or pascal-seconds. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's center line than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strengt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative density" or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Numbers
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive integers Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the ''whole numbers'' refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are ''six'' coins on the table", in which case they are called ''cardinal numbers''. They are also used to put things in order, like "this is the ''third'' largest city in the country", which are called ''ordinal numbers''. Natural numbers are also used as labels, like jersey numbers on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |