|
Pseudo-random Number Sampling
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution. Methods are typically based on the availability of a uniformly distributed PRN generator. Computational algorithms are then used to manipulate a single random variate, ''X'', or often several such variates, into a new random variate ''Y'' such that these values have the required distribution. The first methods were developed for Monte-Carlo simulations in the Manhattan project, published by John von Neumann in the early 1950s. Finite discrete distributions For a discrete probability distribution with a finite number ''n'' of indices at which the probability mass function ''f'' takes non-zero values, the basic sampling algorithm is straightforward. The interval [0, 1) is divided in ''n'' intervals [0, ''f''(1)), [''f''(1), ''f''(1) + ''f''(2)), ... The width of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
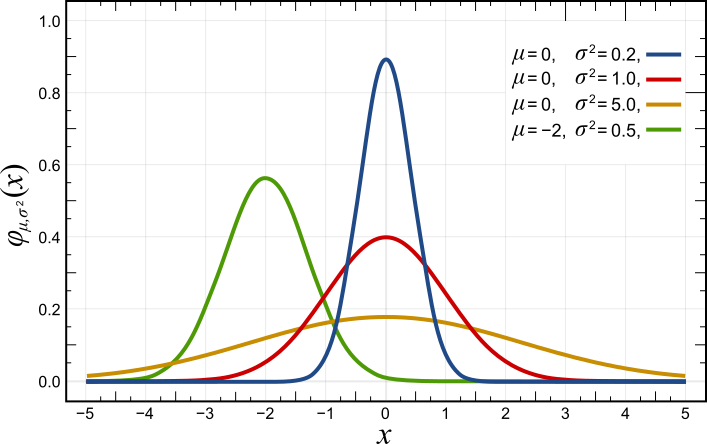
Inverse Transform Sampling
Inverse transform sampling (also known as inversion sampling, the inverse probability integral transform, the inverse transformation method, Smirnov transform, or the golden ruleAalto University, N. Hyvönen, Computational methods in inverse problems. Twelfth lecture https://noppa.tkk.fi/noppa/kurssi/mat-1.3626/luennot/Mat-1_3626_lecture12.pdf) is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function. Inverse transformation sampling takes uniform samples of a number u between 0 and 1, interpreted as a probability, and then returns the largest number x from the domain of the distribution P(X) such that P(-\infty , e.g. from U \sim \mathrm ,1 #Find the inverse of the desired CDF, e.g. F_X^(x). # Compute X=F_X^(u). The computed random variable X has distribution F_X(x). Expressed differently, given a continuous uniform variable U in ,1/math> and an invertible cum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Filter
Particle filters, or sequential Monte Carlo methods, are a set of Monte Carlo algorithms used to solve filtering problems arising in signal processing and Bayesian statistical inference. The filtering problem consists of estimating the internal states in dynamical systems when partial observations are made and random perturbations are present in the sensors as well as in the dynamical system. The objective is to compute the posterior distributions of the states of a Markov process, given the noisy and partial observations. The term "particle filters" was first coined in 1996 by Del Moral about mean-field interacting particle methods used in fluid mechanics since the beginning of the 1960s. The term "Sequential Monte Carlo" was coined by Liu and Chen in 1998. Particle filtering uses a set of particles (also called samples) to represent the posterior distribution of a stochastic process given the noisy and/or partial observations. The state-space model can be nonlinear an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixture Model
In statistics, a mixture model is a probabilistic model for representing the presence of subpopulations within an overall population, without requiring that an observed data set should identify the sub-population to which an individual observation belongs. Formally a mixture model corresponds to the mixture distribution that represents the probability distribution of observations in the overall population. However, while problems associated with "mixture distributions" relate to deriving the properties of the overall population from those of the sub-populations, "mixture models" are used to make statistical inferences about the properties of the sub-populations given only observations on the pooled population, without sub-population identity information. Mixture models should not be confused with models for compositional data, i.e., data whose components are constrained to sum to a constant value (1, 100%, etc.). However, compositional models can be thought of as mixture models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reversible-jump Markov Chain Monte Carlo
In computational statistics, reversible-jump Markov chain Monte Carlo is an extension to standard Markov chain Monte Carlo (MCMC) methodology, introduced by Peter Green, which allows simulation of the posterior distribution on spaces of varying dimensions. Thus, the simulation is possible even if the number of parameters in the model is not known. Let :n_m\in N_m=\ \, be a model indicator and M=\bigcup_^I \R^ the parameter space whose number of dimensions d_m depends on the model n_m. The model indication need not be finite. The stationary distribution is the joint posterior distribution of (M,N_m) that takes the values (m,n_m). The proposal m' can be constructed with a mapping g_ of m and u, where u is drawn from a random component U with density q on \R^. The move to state (m',n_m') can thus be formulated as : (m',n_m')=(g_(m,u),n_m') \, The function : g_:=\Bigg((m,u)\mapsto \bigg((m',u')=\big(g_(m,u),g_(m,u)\big)\bigg)\Bigg) \, must be ''one to one'' and diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
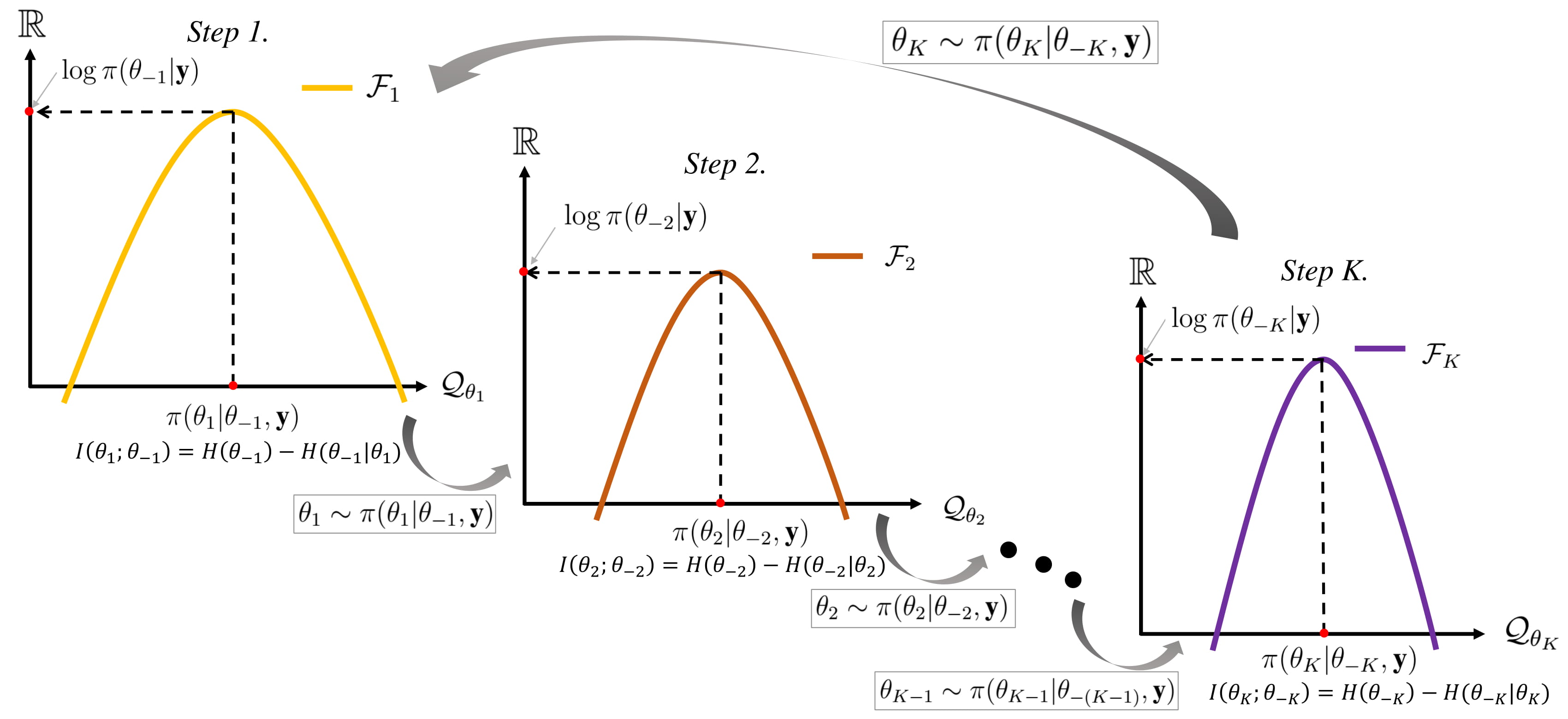
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inference su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metropolis–Hastings Algorithm
In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. This sequence can be used to approximate the distribution (e.g. to generate a histogram) or to compute an integral (e.g. an expected value). Metropolis–Hastings and other MCMC algorithms are generally used for sampling from multi-dimensional distributions, especially when the number of dimensions is high. For single-dimensional distributions, there are usually other methods (e.g. adaptive rejection sampling) that can directly return independent samples from the distribution, and these are free from the problem of autocorrelated samples that is inherent in MCMC methods. History The algorithm was named after Nicholas Metropolis and W.K. Hastings. Metropolis was the first author to appear on the list of authors of the 1953 article '' Equatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm. Application domains MCMC methods are primarily used for calculating numerical approximations of multi-dimensional integrals, for example in Bayesian statistics, computational physics, computational biology and computational linguistics. In Bayesian statistics, the recent development of MCMC methods has made it possible to compute large hierarchical models that require integrations over hundreds to thousands of unknown parameters. In rare even ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlated
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution Random Number Generator
In statistics and computer software, a convolution random number generator is a pseudo-random number sampling method that can be used to generate random variates from certain classes of probability distribution. The particular advantage of this type of approach is that it allows advantage to be taken of existing software for generating random variates from other, usually non-uniform, distributions. However, faster algorithms may be obtainable for the same distributions by other more complicated approaches. A number of distributions can be expressed in terms of the (possibly weighted) sum of two or more random variables from other distributions. (The distribution of the sum is the convolution of the distributions of the individual random variables). Example Consider the problem of generating a random variable with an Erlang distribution, X\ \sim \operatorname(k, \theta). Such a random variable can be defined as the sum of ''k'' random variables each with an exponential distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ziggurat Algorithm
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The algorithm is used to generate values from a monotonically decreasing probability distribution. It can also be applied to symmetric unimodal distributions, such as the normal distribution, by choosing a value from one half of the distribution and then randomly choosing which half the value is considered to have been drawn from. It was developed by George Marsaglia and others in the 1960s. A typical value produced by the algorithm only requires the generation of one random floating-point value and one random table index, followed by one table lookup, one multiply operation and one comparison. Sometimes (2.5% of the time, in the case of a normal or exponential distribution when using typical ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
