|
Convolution Random Number Generator
In statistics and computer software, a convolution random number generator is a pseudo-random number sampling method that can be used to generate random variates from certain classes of probability distribution. The particular advantage of this type of approach is that it allows advantage to be taken of existing software for generating random variates from other, usually non-uniform, distributions. However, faster algorithms may be obtainable for the same distributions by other more complicated approaches. A number of distributions can be expressed in terms of the (possibly weighted) sum of two or more random variables from other distributions. (The distribution of the sum is the convolution of the distributions of the individual random variables). Example Consider the problem of generating a random variable with an Erlang distribution, X\ \sim \operatorname(k, \theta). Such a random variable can be defined as the sum of ''k'' random variables each with an exponential distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Software
Software is a set of computer programs and associated documentation and data. This is in contrast to hardware, from which the system is built and which actually performs the work. At the lowest programming level, executable code consists of machine language instructions supported by an individual processor—typically a central processing unit (CPU) or a graphics processing unit (GPU). Machine language consists of groups of binary values signifying processor instructions that change the state of the computer from its preceding state. For example, an instruction may change the value stored in a particular storage location in the computer—an effect that is not directly observable to the user. An instruction may also invoke one of many input or output operations, for example displaying some text on a computer screen; causing state changes which should be visible to the user. The processor executes the instructions in the order they are provided, unless it is instructed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-random Number Sampling
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution. Methods are typically based on the availability of a uniformly distributed PRN generator. Computational algorithms are then used to manipulate a single random variate, ''X'', or often several such variates, into a new random variate ''Y'' such that these values have the required distribution. The first methods were developed for Monte-Carlo simulations in the Manhattan project, published by John von Neumann in the early 1950s. Finite discrete distributions For a discrete probability distribution with a finite number ''n'' of indices at which the probability mass function ''f'' takes non-zero values, the basic sampling algorithm is straightforward. The interval [0, 1) is divided in ''n'' intervals [0, ''f''(1)), [''f''(1), ''f''(1) + ''f''(2)), ... The width of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variate
In probability and statistics, a random variate or simply variate is a particular outcome of a ''random variable'': the random variates which are other outcomes of the same random variable might have different values (random numbers). A random deviate or simply deviate is the difference of random variate with respect to the distribution central location (e.g., mean), often divided by the standard deviation of the distribution (i.e., as a standard score). Random variates are used when simulating processes driven by random influences (stochastic processes). In modern applications, such simulations would derive random variates corresponding to any given probability distribution from computer procedures designed to create random variates corresponding to a uniform distribution, where these procedures would actually provide values chosen from a uniform distribution of pseudorandom numbers. Procedures to generate random variates corresponding to a given distribution are known as p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a random var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erlang Distribution
The Erlang distribution is a two-parameter family of continuous probability distributions with support x \in independent exponential distribution">exponential variables with mean 1/\lambda each. Equivalently, it is the distribution of the time until the ''k''th event of a Poisson process with a rate of \lambda. The Erlang and Poisson distributions are complementary, in that while the Poisson distribution counts the number of events that occur in a fixed amount of time, the Erlang distribution counts the amount of time until the occurrence of a fixed number of events. When k=1, the distribution simplifies to the exponential distribution. The Erlang distribution is a special case of the gamma distribution wherein the shape of the distribution is discretised. The Erlang distribution was developed by A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. This work on telephone traffic engineering has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \lambda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
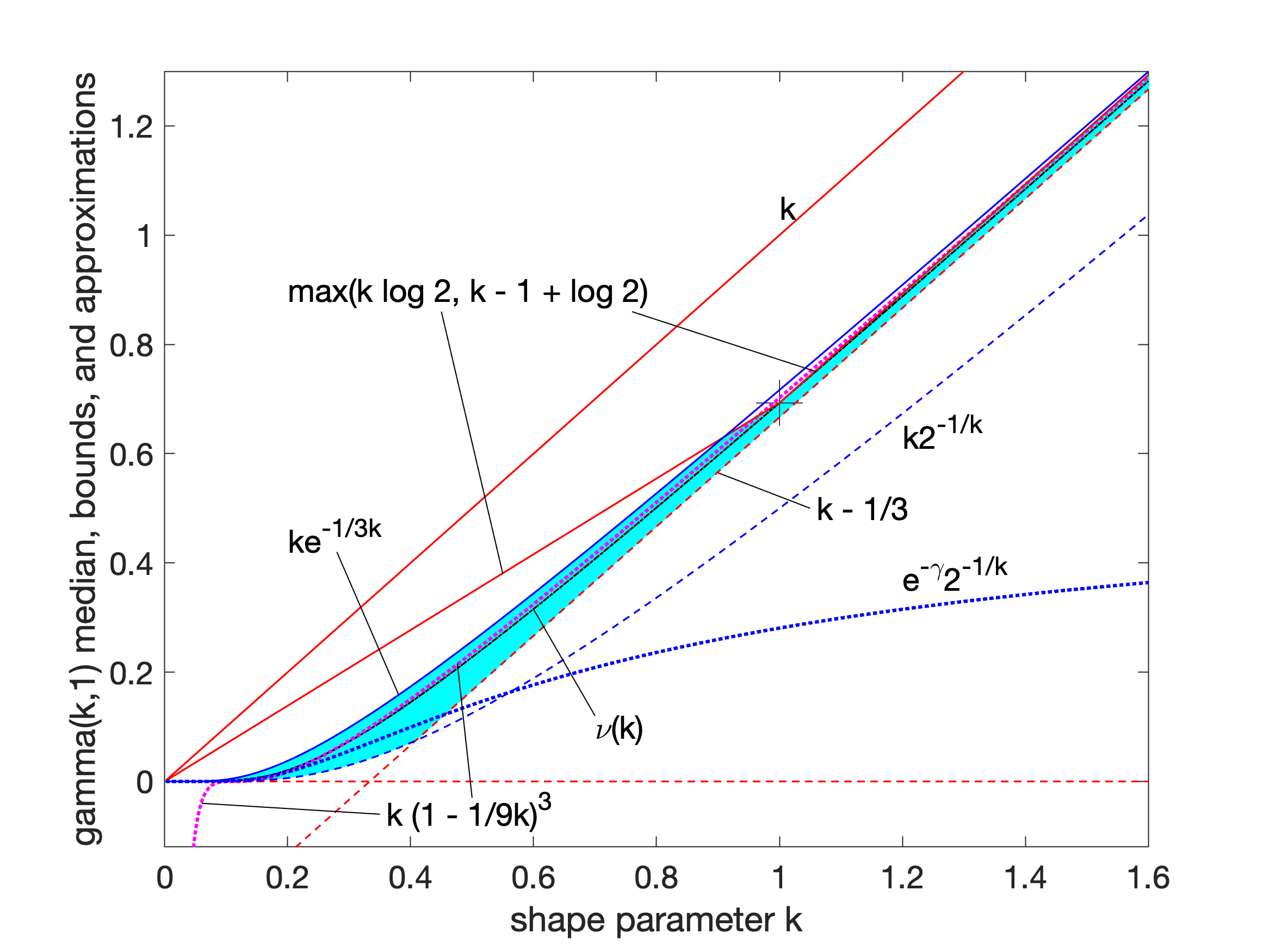
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moments, using the method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimators of shape often involve higher-order statistics (non-linear functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Computer Software")
.svg "Click for more on -> Probability Distribution")
