|
Proportional System
Proportionality, proportion or proportional may refer to: Mathematics * Proportionality (mathematics), the property of two variables being in a multiplicative relation to a constant * Ratio, of one quantity to another, especially of a part compared to a whole ** Fraction (mathematics) * Aspect ratio or proportions * Proportional division, a kind of fair division * Percentage, a number or ratio expressed as a fraction of 100 Science and art * Proportional fonts * Proportionally fair, a scheduling algorithm * Proportional control, a type of linear feedback control system Other uses * Proportionality (law), a legal principle * Proportion (architecture), describes the relationships between elements of a design * Body proportions, in art, the study of relation of human body parts to each other and the whole See also * Proportional representation Proportional representation (PR) refers to a type of electoral system under which subgroups of an electorate are reflected proportionat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality. This definition is commonly extended to related varying quantities, which are often called ''variables''. This meaning of ''variable'' is not the common meaning of the term in mathematics (see variable (mathematics)); these two different concepts share the same name for historical reasons. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7). The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be Positive integer, positive. A ratio may be specified either by giving both constituting numbers, written as "''a'' to ''b''" or "''a'':''b''", or by giving just the value of their quotient Equal quotients correspond to equal ratios. Consequently, a ratio may be considered as an ordered pair of numbers, a Fraction (mathematics), fraction with the first number in the numerator and the second in the denom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fraction (mathematics)
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: \tfrac and \tfrac) consists of a numerator, displayed above a line (or before a slash like ), and a non-zero denominator, displayed below (or after) that line. Numerators and denominators are also used in fractions that are not ''common'', including compound fractions, complex fractions, and mixed numerals. In positive common fractions, the numerator and denominator are natural numbers. The numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. The denominator cannot be zero, because zero parts can never make up a whole. For example, in the fraction , the numerator 3 indicates that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Division
A proportional division is a kind of fair division in which a resource is divided among ''n'' partners with subjective valuations, giving each partner at least 1/''n'' of the resource by his/her own subjective valuation. Proportionality was the first fairness criterion studied in the literature; hence it is sometimes called "simple fair division". It was first conceived by Steinhaus. Example Consider a land asset that has to be divided among 3 heirs: Alice and Bob who think that it's worth 3 million dollars, and George who thinks that it's worth $4.5M. In a proportional division, Alice receives a land-plot that she believes to be worth at least $1M, Bob receives a land-plot that ''he'' believes to be worth at least $1M (even though Alice may think it is worth less), and George receives a land-plot that he believes to be worth at least $1.5M. Existence A proportional division does not always exist. For example, if the resource contains several indivisible items and the number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percentage
In mathematics, a percentage (from la, per centum, "by a hundred") is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also used. A percentage is a dimensionless number (pure number); it has no unit of measurement. Examples For example, 45% (read as "forty-five per cent") is equal to the fraction , the ratio 45:55 (or 45:100 when comparing to the total rather than the other portion), or 0.45. Percentages are often used to express a proportionate part of a total. (Similarly, one can also express a number as a fraction of 1,000, using the term "per mille" or the symbol "".) Example 1 If 50% of the total number of students in the class are male, that means that 50 out of every 100 students are male. If there are 500 students, then 250 of them are male. Example 2 An increase of $0.15 on a price of $2.50 is an increase by a fraction of = 0.06. Expressed as a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Fonts
A typeface (or font family) is the design of lettering that can include variations in size, weight (e.g. bold), slope (e.g. italic), width (e.g. condensed), and so on. Each of these variations of the typeface is a font. There are thousands of different typefaces in existence, with new ones being developed constantly. The art and craft of designing typefaces is called ''type design''. Designers of typefaces are called ''type designers'' and are often employed by ''type foundries''. In desktop publishing, type designers are sometimes also called ''font developers'' or ''font designers''. Every typeface is a collection of glyphs, each of which represents an individual letter, number, punctuation mark, or other symbol. The same glyph may be used for characters from different scripts, e.g. Roman uppercase A looks the same as Cyrillic uppercase А and Greek uppercase alpha. There are typefaces tailored for special applications, such as cartography, astrology or mathematics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionally Fair
Proportional-fair scheduling is a compromise-based scheduling algorithm. It is based upon maintaining a balance between two competing interests: Trying to maximize total throughput of the network (wired or not) while at the same time allowing all users at least a minimal level of service. This is done by assigning each data flow a data rate or a scheduling priority (depending on the implementation) that is inversely proportional to its anticipated resource consumption.Guowang Miao, Jens Zander, Ki Won Sung, and Ben Slimane, Fundamentals of Mobile Data Networks, Cambridge University Press, , 2016. Weighted fair queuing Proportionally fair scheduling can be achieved by means of weighted fair queuing (WFQ), by setting the scheduling weights for data flow i to w_i = 1 / c_i, where the cost c_i is the amount of consumed resources per data bit. For instance: * In CDMA spread spectrum cellular networks, the cost may be the required energy per bit in the transmit power control (the incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
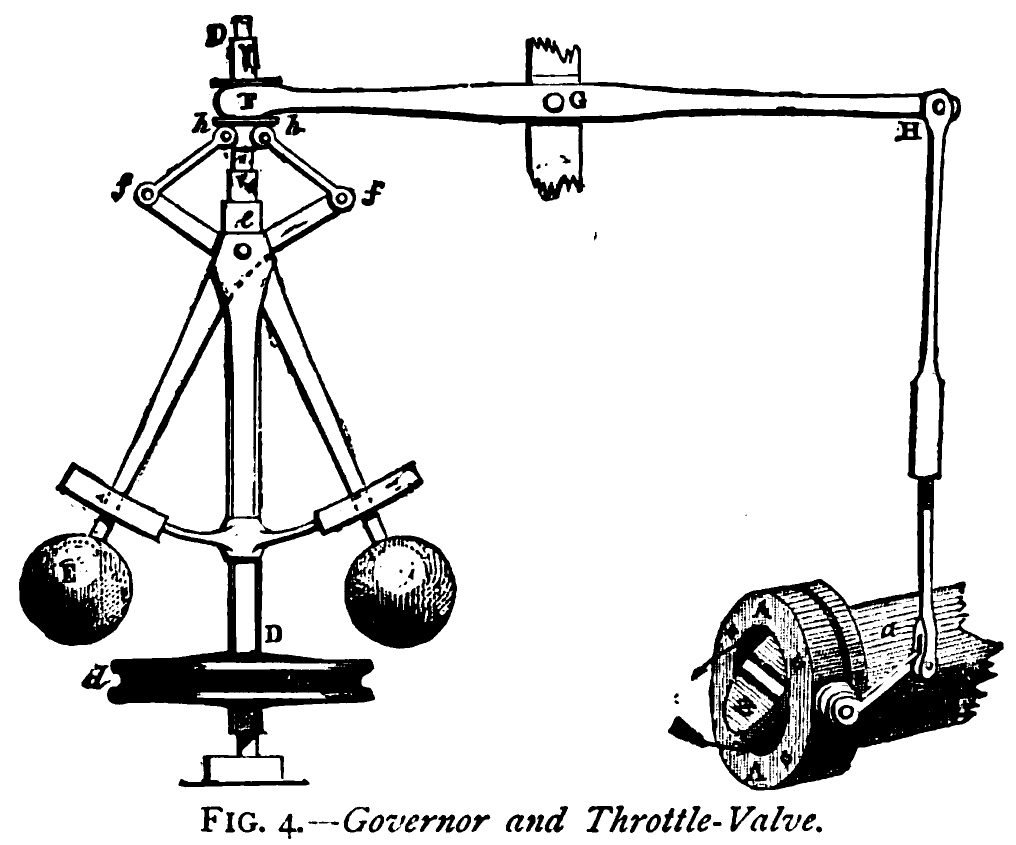
Proportional Control
Proportional control, in engineering and process control, is a type of linear feedback control system in which a correction is applied to the controlled variable, and the size of the correction is proportional to the difference between the desired value ( setpoint, SP) and the measured value (process variable, PV). Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor. The proportional control concept is more complex than an on–off control system such as a bi-metallic domestic thermostat, but simpler than a proportional–integral–derivative (PID) control system used in something like an automobile cruise control. On–off control will work where the overall system has a relatively long response time, but can result in instability if the system being controlled has a rapid response time. Proportional control overcomes this by modulating the output to the controlling device, such as a control valve at a level which avoids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (law)
Proportionality is a general principle in law which covers several separate (although related) concepts: *The concept of proportionality is used as a criterion of fairness and justice in statutory interpretation processes, especially in constitutional law, as a logical method intended to assist in discerning the correct balance between the restriction imposed by a corrective measure and the severity of the nature of the prohibited act. *Within criminal law, the concept is used to convey the idea that the punishment of an offender should fit the crime. *Under international humanitarian law governing the legal use of force in an armed conflict, ''proportionality'' and '' distinction'' are important factors in assessing military necessity. *Under the United Kingdom's Civil Procedure Rules, costs must be "proportionately and reasonably incurred", or "proportionate and reasonable in amount", if they are to form part of a court ruling on costs. Proportionality as a general principle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportion (architecture)
Proportion is a central principle of architectural theory and an important connection between mathematics and art. It is the visual effect of the relationships of the various objects and spaces that make up a structure to one another and to the whole. These relationships are often governed by multiples of a standard unit of length known as a "module". Proportion in architecture was discussed by Vitruvius, Leon Battista Alberti, Andrea Palladio, and Le Corbusier among others. Roman architecture Vitruvius Architecture in Roman antiquity was rarely documented except in the writings of Vitruvius' treatise '' De architectura''. Vitruvius served as an engineer under Julius Caesar during the first Gallic Wars (58–50 BC). The treatise was dedicated to Emperor Augustus. As Vitruvius defined the concept in the first chapters of the treatise, he mentioned the three prerequisites of architecture are firmness (''firmitas''), commodity (''utilitas''), and delight (''venustas''), whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Proportions
While there is significant variation in anatomical proportions between people, certain body proportions have become canonical in figurative art. The study of body proportions, as part of the study of artistic anatomy, explores the relation of the elements of the human body to each other and to the whole. These ratios are used in depictions of the human figure and may become part of an artistic canon of body proportion within a culture. Academic art of the nineteenth century demanded close adherence to these reference metrics and some artists in the early twentieth century rejected those constraints and consciously mutated them. Basics of human proportions It is usually important in figure drawing to draw the human figure in proportion. Though there are subtle differences between individuals, human proportions fit within a fairly standard range though artists have historically tried to create idealised standards that have varied considerably over time, according to era and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |