|
Projective Cone
A projective cone (or just cone) in projective geometry is the union of all lines that intersect a projective subspace ''R'' (the apex of the cone) and an arbitrary subset ''A'' (the basis) of some other subspace ''S'', disjoint from ''R''. In the special case that ''R'' is a single point, ''S'' is a plane, and ''A'' is a conic section on ''S'', the projective cone is a conical surface; hence the name. Definition Let ''X'' be a projective space over some field ''K'', and ''R'', ''S'' be disjoint subspaces of ''X''. Let ''A'' be an arbitrary subset of ''S''. Then we define ''RA'', the cone with top ''R'' and basis ''A'', as follows : * When ''A'' is empty, ''RA'' = ''A''. * When ''A'' is not empty, ''RA'' consists of all those points on a line connecting a point on ''R'' and a point on ''A''. Properties * As ''R'' and ''S'' are disjoint, one may deduce from linear algebra and the definition of a projective space that every point on ''RA'' not in ''R'' or ''A'' is on exactly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called " points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Surface
In geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the ''apex'' or ''vertex'' — and any point of some fixed space curve — the ''directrix'' — that does not contain the apex. Each of those lines is called a ''generatrix'' of the surface. Every conic surface is ruled and developable. In general, a conical surface consists of two congruent unbounded halves joined by the apex. Each half is called a nappe, and is the union of all the rays that start at the apex and pass through a point of some fixed space curve. (In some cases, however, the two nappes may intersect, or even coincide with the full surface.) Sometimes the term "conical surface" is used to mean just one nappe. If the directrix is a circle C, and the apex is located on the circle's ''axis'' (the line that contains the center of C and is perpendicular to its plane), one obtains the ''right circular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In classical Euclidean geometry, a point is a primitive notion that models an exact location in space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space. Being a primitive notion means that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy; for example, ''"there is exactly one line that passes through two different points"''. Points in Euclidean geometry Points, considered within the framework of Euclidean geometry, are one of the most fundamental objects. Euclid originally defined the point as "that which has no part". In two-dimensional Euclidean space, a point is represented by an ordered pair (, ) of numbers, where the first number conventionally represents the horizontal and is often denoted by , and the second number conventionally represents the vertical and is often denoted by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod when is a prime number. The ''order'' of a finite field is its number of elements, which is either a prime number or a prime power. For every prime number and every positive integer there are fields of order p^k, all of which are isomorphic. Finite fields are fundamental in a number of areas of mathematics and computer science, including number theory, algebraic geometry, Galois theory, finite geometry, cryptography and coding theory. Properties A finite field is a finite set which is a field; this means that multiplication, addition, subtraction and division (excluding division by zero) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
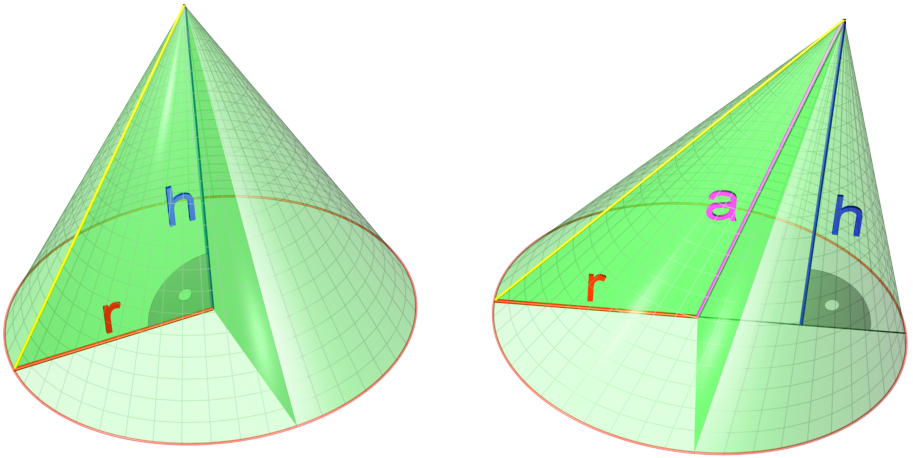
Cone (geometry)
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of hal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone (algebraic Geometry)
In algebraic geometry, a cone is a generalization of a vector bundle. Specifically, given a scheme ''X'', the relative Spec :C = \operatorname_X R of a quasi-coherent graded ''O''''X''-algebra ''R'' is called the cone or affine cone of ''R''. Similarly, the relative Proj :\mathbb(C) = \operatorname_X R is called the projective cone of ''C'' or ''R''. Note: The cone comes with the \mathbb_m-action due to the grading of ''R''; this action is a part of the data of a cone (whence the terminology). Examples *If ''X'' = Spec ''k'' is a point and ''R'' is a homogeneous coordinate ring, then the affine cone of ''R'' is the (usual) affine cone over the projective variety corresponding to ''R''. *If R = \bigoplus_0^\infty I^n/I^ for some ideal sheaf ''I'', then \operatorname_X R is the normal cone to the closed scheme determined by ''I''. *If R = \bigoplus_0^\infty L^ for some line bundle ''L'', then \operatorname_X R is the total space of the dual of ''L''. *More generally, given a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone (topology)
In topology, especially algebraic topology, the cone of a topological space X is intuitively obtained by stretching ''X'' into a cylinder and then collapsing one of its end faces to a point. The cone of X is denoted by CX or by \operatorname(X). Definitions Formally, the cone of ''X'' is defined as: :CX = (X \times ,1\cup_p v\ =\ \varinjlim \bigl( (X \times ,1 \hookleftarrow (X\times \) \xrightarrow v\bigr), where v is a point (called the vertex of the cone) and p is the projection to that point. In other words, it is the result of attaching the cylinder X \times ,1/math> by its face X\times\ to a point v along the projection p: \bigl( X\times\ \bigr)\to v. If X is a non-empty compact subspace of Euclidean space, the cone on X is homeomorphic to the union of segments from X to any fixed point v \not\in X such that these segments intersect only by v itself. That is, the topological cone agrees with the geometric cone for compact spaces when the latter is defined. Ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone (linear Algebra)
In linear algebra, a ''cone''—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, is a cone if x\in C implies sx\in C for every . When the scalars are real numbers, or belong to an ordered field, one generally calls a cone a subset of a vector space that is closed under multiplication by a ''positive scalar''. In this context, a convex cone is a cone that is closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. In this article, only the case of scalars in an ordered field is considered. Definition A subset ''C'' of a vector space ''V'' over an ordered field ''F'' is a cone (or sometimes called a linear cone) if for each ''x'' in ''C'' and positive scalar ''α'' in ''F'', the product ''αx'' is in ''C''. Note that some authors define co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruled Surface
In geometry, a surface is ruled (also called a scroll) if through every point of there is a straight line that lies on . Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space. A ruled surface can be described as the set of points swept by a moving straight line. For example, a cone is formed by keeping one point of a line fixed whilst moving another point along a circle. A surface is ''doubly ruled'' if through every one of its points there are two distinct lines that lie on the surface. The hyperbolic paraboloid and the hyperboloid of one sheet are doubly ruled surfaces. The plane is the only surface which contains at least three distinct lines through each of its points . The properties of being ruled or doubly ruled are preserved by projective maps, and therefore are concepts of projective geometry. In algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |