|
Polar Distance (astronomy)
In the celestial equatorial coordinate system Σ(α, δ) in astronomy, polar distance (PD) is an angular distance of a celestial object on its meridian measured from the celestial pole, similar to the way declination (dec, δ) is measured from the celestial equator. Definition Polar distance in celestial navigation is the angle between the pole and the Position of body on its Declination. Referring to diagram: P- Pole , WQE- Equator , Z - Zenith of observer , Y- Lower meridian passage of body X- Upper meridian passage of body Here body will be on declination circle ( XY). The distance between PY or PX will be the Polar distance of the body. NP=ZQ=Latitude of observer NY and NX will be the True altitude of body at that instant. Polar distance (PD) = 90° ± δ Polar distances are expressed in degrees and cannot exceed 180° in magnitude. An object on the celestial equator has a PD of 90°. Polar distance is affected by the precession of the equinoxes. If the pola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
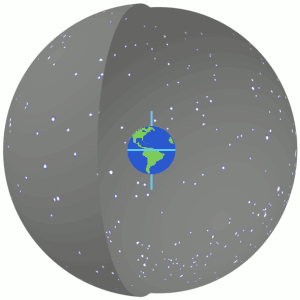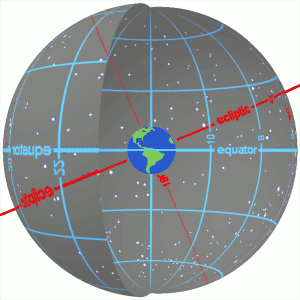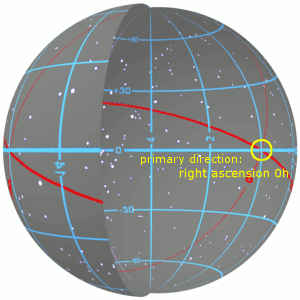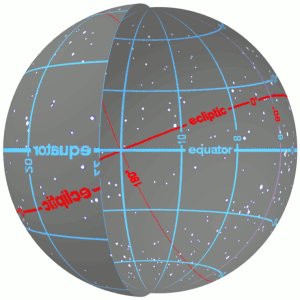
Equatorial Coordinate System
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the vernal equinox, and a right-handed convention. The origin at the centre of Earth means the coordinates are ''geocentric'', that is, as seen from the centre of Earth as if it were transparent. The fundamental plane and the primary direction mean that the coordinate system, while aligned with Earth's equator and pole, does not rotate with the Earth, but remains relatively fixed against the background stars. A right-handed convention means that coordinates increase northward from and eastward around the fundamental plane. Primary direction This description of the orientation of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or ''normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the ocean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point where the parabola intersects its axis of symmetry is called the "vertex" and is the point where the parabola is most sharply curved. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sundial
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude. The term ''sundial'' can refer to any device that uses the Sun's altitude or azimut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields. History A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the oldest gnomon known in China. The gnomon was widely used in ancient China from the second century BC onward in order to determine the changes in seasons, orientation, and geographical latitude. The ancient Chinese used shadow measurements for creating calendars that are mentioned in several ancient texts. According to the collection of Zhou Chinese poetic anthologies ''Classic of Poetry'', one of the distant ancestors of King Wen of the Zhou dynasty used to measure gnomon shadow lengths to determine the orientation around the 14th century BC. The ancient Greek philosopher Anaximander (610–546 BC) is credited with introducing this Babylonian instrument to the Ancient Greeks. The ancient Greek mathematician and astronomer Oenopides used the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shadow
A shadow is a dark area where light from a light source is blocked by an opaque object. It occupies all of the three-dimensional volume behind an object with light in front of it. The cross section of a shadow is a two-dimensional silhouette, or a reverse projection of the object blocking the light. Point and non-point light sources A point source of light casts only a simple shadow, called an "umbra". For a non-point or "extended" source of light, the shadow is divided into the umbra, penumbra, and antumbra. The wider the light source, the more blurred the shadow becomes. If two penumbras overlap, the shadows appear to attract and merge. This is known as the shadow blister effect. The outlines of the shadow zones can be found by tracing the rays of light emitted by the outermost regions of the extended light source. The umbra region does not receive any direct light from any part of the light source and is the darkest. A viewer located in the umbra region cannot directly se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precession Of The Equinoxes
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac''. Sausalito: University Science Books. p. 99. This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—nutation and polar motion—are much smaller in magnitude. Earth's precession was historically called the precession of the equinoxes, because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest include planets, natural satellite, moons, stars, nebulae, galaxy, galaxies, and comets. Relevant phenomena include supernova explosions, gamma ray bursts, quasars, blazars, pulsars, and cosmic microwave background radiation. More generally, astronomy studies everything that originates beyond atmosphere of Earth, Earth's atmosphere. Cosmology is a branch of astronomy that studies the universe as a whole. Astronomy is one of the oldest natural sciences. The early civilizations in recorded history made methodical observations of the night sky. These include the Babylonian astronomy, Babylonians, Greek astronomy, Greeks, Indian astronomy, Indians, Egyptian astronomy, Egyptians, Chinese astronomy, Chinese, Maya civilization, Maya, and many anc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |