|
Polana Family
The Nysa family (adj. ''Nysian''; FIN: 405) is part of the Nysa–Polana complex, the largest cluster of asteroid families in the asteroid belt. It is located in the inner region of the asteroid belt, orbiting the Sun between 2.41 and 2.5 AU. Asteroids in this complex have eccentricities between 0.12 and 0.21 and inclinations of 1.4 to 4.3. The family derives its name from its most massive member, 44 Nysa. It has also been known as the Hertha family ''(adj. Herthian)'' named after 135 Hertha. Subdivision Asteroids in this complex are typically divided into the stony Nysa and carbonaceous Polana subgroups, two mineralogically different families: * The much brighter S-type Nysian subgroup (i.e. the Nysa family, in the narrower sense) includes 44 Nysa and 135 Hertha. * In the low- albedo subgroup of the complex lies the Polana family ''(adj Polanian)'', a family of dark F-type asteroids named after 142 Polana, the largest asteroid in this section. More recentl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Family Identification Number
An asteroid family is a population of asteroids that share similar proper orbital elements, such as semimajor axis, eccentricity (orbit), eccentricity, and orbital inclination. The members of the families are thought to be Collisional family, fragments of past asteroid collisions. An asteroid family is a more specific term than list of minor-planet groups, asteroid group whose members, while sharing some broad orbital characteristics, may be otherwise unrelated to each other. General properties Large prominent families contain several hundred recognized asteroids (and many more smaller objects which may be either not-yet-analyzed, or not-yet-discovered). Small, compact families may have only about ten identified members. About 33% to 35% of asteroids in the main belt are family members. There are about 20 to 30 reliably recognized families, with several tens of less certain groupings. Most asteroid families are found in the main belt, main asteroid belt, although several famil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * circular orbit: ''e'' = 0 * elliptic orbit: 0 < ''e'' < 1 * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5075 Goryachev
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has attained significance throughout history in part because typical humans have five digits on each hand. In mathematics 5 is the third smallest prime number, and the second super-prime. It is the first safe prime, the first good prime, the first balanced prime, and the first of three known Wilson primes. Five is the second Fermat prime and the third Mersenne prime exponent, as well as the third Catalan number, and the third Sophie Germain prime. Notably, 5 is equal to the sum of the ''only'' consecutive primes, 2 + 3, and is the only number that is part of more than one pair of twin primes, ( 3, 5) and (5, 7). It is also a sexy prime with the fifth prime number and first prime repunit, 11. Five is the third factorial prime, an alternating factorial, and an Eisenstein prime with no imaginary part and real part of the form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4797 Ako
4797 Ako, provisional designation , is a stony Nysian asteroid from the inner regions of the asteroid belt, approximately 5 kilometers in diameter. It was discovered on 30 September 1989, by the Japanese astronomers Toshiro Nomura and Kōyō Kawanishi at the Minami-Oda Observatory (), Japan. The asteroid was named for the Japanese city of Akō. Orbit and classification ''Ako'' is a member of the stony subgroup of the Nysa family, which is named after its largest member 44 Nysa. It orbits the Sun in the inner main-belt at a distance of 2.0–2.9 AU once every 3 years and 9 months (1,369 days). Its orbit has an eccentricity of 0.18 and an inclination of 2 ° with respect to the ecliptic. In 1978, it was first identified as at Palomar Observatory, extending the body's observation arc by 11 years prior to its official discovery observation at Minami-Oda Observatory. Physical characteristics Rotation period A rotational lightcurve of ''Ako'' was obtained for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
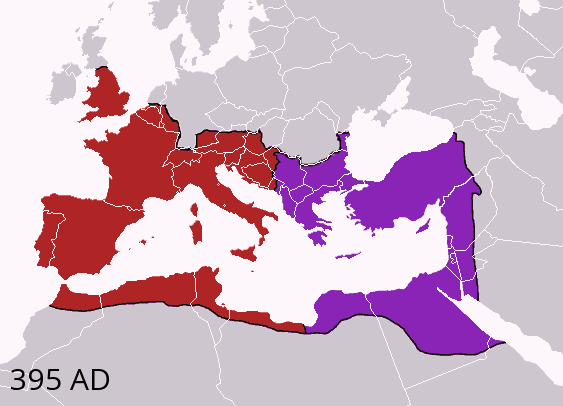
3952 Russellmark
__NOTOC__ Year 395 ( CCCXCV) was a common year starting on Monday (link will display the full calendar) of the Julian calendar. At the time, it was known as the Year of the Consulship of Olybrius and Probinus (or, less frequently, year 1148 ''Ab urbe condita''). The denomination 395 for this year has been used since the early medieval period, when the Anno Domini calendar era became the prevalent method in Europe for naming years. Events By place Roman Empire * January 17 – Emperor Theodosius I, age 48, dies of a disease involving severe edema in Milan. The Roman Empire is again divided into an eastern and a western half. The Eastern Roman Empire is centered in Constantinople under Arcadius, son of Theodosius, and the Western Roman Empire in Mediolanum under his brother Honorius. * April 27 – Arcadius marries Aelia Eudoxia, daughter of the Frankish general Flavius Bauto (without the knowledge or consent of Rufinus, Praetorian prefect of the East). His s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3467 Bernheim
While the future cannot be predicted with certainty, present understanding in various scientific fields allows for the prediction of some far-future events, if only in the broadest outline. These fields include astrophysics, which studies how planets and stars form, interact, and die; particle physics, which has revealed how matter behaves at the smallest scales; evolutionary biology, which studies how life evolves over time; plate tectonics, which shows how continents shift over millennia; and sociology, which examines how human societies and cultures evolve. The far future begins after the current millennium comes to an end, starting with the 4th millennium in 3001 CE, until the furthest reaches of future time. These timelines include alternative future events that address unresolved scientific questions, such as whether humans will become extinct, whether the Earth survives when the Sun expands to become a red giant and whether proton decay will be the eventual end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3172 Hirst
Year 317 ( CCCXVII) was a common year starting on Tuesday (link will display the full calendar) of the Julian calendar. At the time, it was known as the Year of the Consulship of Gallicanus and Bassus (or, less frequently, year 1070 ''Ab urbe condita''). The denomination 317 for this year has been used since the early medieval period, when the Anno Domini calendar era became the prevalent method in Europe for naming years. Events By place Roman Empire * March 1 – Emperor Constantine the Great and co-emperor Licinius elevate their sons Crispus, Constantine II (being still a baby) and Licinius II to '' Caesars''. After this arrangement Constantine rules the dioceses Pannonia and Macedonia, and establishes his residence at Sirmium, from where he prepares a campaign against the Goths and Sarmatians. * Licinius recognizes Constantine I as senior emperor and executes Valerius Valens. Asia * Sixteen Kingdoms: Jingwen (later Yuan of Jin) flees with remnants of the Jin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3069 Heyrovsky
3 (three) is a number, numeral and digit. It is the natural number following 2 and preceding 4, and is the smallest odd prime number and the only prime preceding a square number. It has religious or cultural significance in many societies. Evolution of the Arabic digit The use of three lines to denote the number 3 occurred in many writing systems, including some (like Roman and Chinese numerals) that are still in use. That was also the original representation of 3 in the Brahmic (Indian) numerical notation, its earliest forms aligned vertically. However, during the Gupta Empire the sign was modified by the addition of a curve on each line. The Nāgarī script rotated the lines clockwise, so they appeared horizontally, and ended each line with a short downward stroke on the right. In cursive script, the three strokes were eventually connected to form a glyph resembling a with an additional stroke at the bottom: ३. The Indian digits spread to the Caliphate in the 9th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3048 Guangzhou
3 (three) is a number, numeral and digit. It is the natural number following 2 and preceding 4, and is the smallest odd prime number and the only prime preceding a square number. It has religious or cultural significance in many societies. Evolution of the Arabic digit The use of three lines to denote the number 3 occurred in many writing systems, including some (like Roman and Chinese numerals) that are still in use. That was also the original representation of 3 in the Brahmic (Indian) numerical notation, its earliest forms aligned vertically. However, during the Gupta Empire the sign was modified by the addition of a curve on each line. The Nāgarī script rotated the lines clockwise, so they appeared horizontally, and ended each line with a short downward stroke on the right. In cursive script, the three strokes were eventually connected to form a glyph resembling a with an additional stroke at the bottom: ३. The Indian digits spread to the Caliphate in the 9th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2710 Veverka
71 may refer to: * 71 (number) * one of the years 71 BC, AD 71 AD 71 ( LXXI) was a common year starting on Tuesday (link will display the full calendar) of the Julian calendar. At the time, it was known as the Year of the Consulship of Vespasian and Nerva (or, less frequently, year 824 '' Ab urbe condita ..., 1971, 2071 * 71'' (film), 2014 British film set in Belfast in 1971 * '' 71: Into the Fire'', 2010 South Korean film See also * List of highways numbered * {{Number disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2509 Chukotka
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has attained significance throughout history in part because typical humans have five digits on each hand. In mathematics 5 is the third smallest prime number, and the second super-prime. It is the first safe prime, the first good prime, the first balanced prime, and the first of three known Wilson primes. Five is the second Fermat prime and the third Mersenne prime exponent, as well as the third Catalan number, and the third Sophie Germain prime. Notably, 5 is equal to the sum of the ''only'' consecutive primes, 2 + 3, and is the only number that is part of more than one pair of twin primes, ( 3, 5) and (5, 7). It is also a sexy prime with the fifth prime number and first prime repunit, 11. Five is the third factorial prime, an alternating factorial, and an Eisenstein prime with no imaginary part and real part of the form 3p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |