|
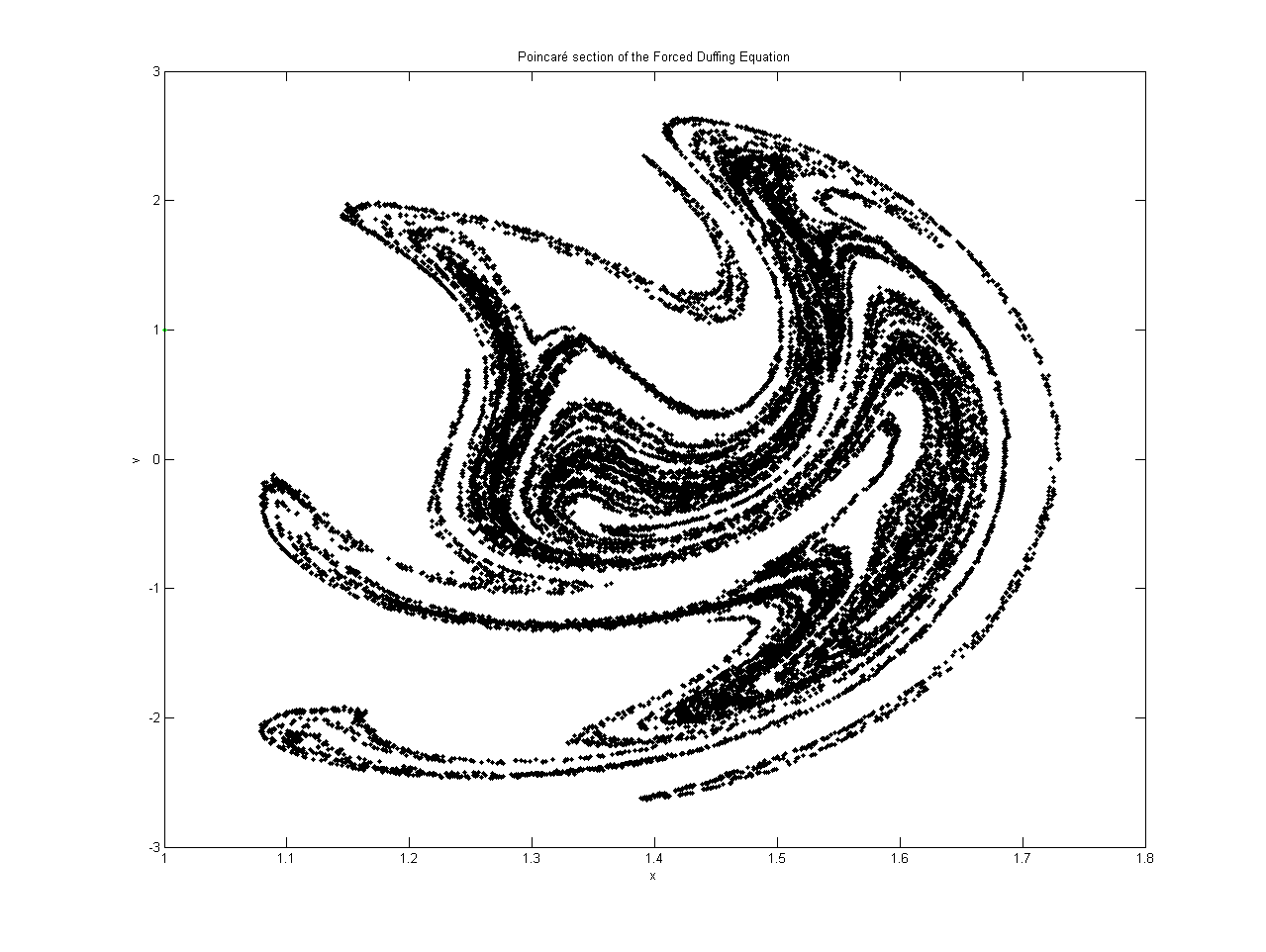
Poincaré Plot
A Poincaré plot, named after Henri Poincaré, is a type of recurrence plot used to quantify self-similarity in processes, usually periodic functions. It is also known as a return map. Poincaré plots can be used to distinguish chaos from randomness by embedding a data set in a higher-dimensional state space. Given a time series of the form : x_t, x_, x_, \ldots, a return map in its simplest form first plots (''x''''t'', ''x''''t''+1), then plots (''x''''t''+1, ''x''''t''+2), then (''x''''t''+2, ''x''''t''+3), and so on. Applications in electrocardiography An electrocardiogram (ECG) is a tracing of the voltage changes in the chest generated by the heart, whose contraction in a normal person is triggered by an electrical impulse that originates in the sinoatrial node. The ECG normally consists of a series of waves, labeled the P, Q, R, S and T waves. The P wave represents depolarization of the atria, the Q-R-S series of waves depolarization of the ventricles a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is also considered to be one of the founders of the field of topology. Poincaré made clear the importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré disc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heart Rate Turbulence
Heart rate turbulence (HRT) is the return to equilibrium of heart rate after a premature ventricular contraction (PVC). It consists of a brief speed-up in heart rate, followed by a slow decrease back to the baseline rate. An important feature of HRT is that PVCs occur naturally in most adults, so measuring the characteristics of a given person's HRT offers a non-invasive way to evaluate his or her cardiac function without applying artificial external stimuli. The measured values of HRT parameters have been shown to be a statistically significant predictor of the probability of dying from cardiac disease after a patient suffers a myocardial infarction. HRT can also be used to predict death in patients with congestive heart failure from a lethal arrhythmia. HRT has nothing to do with turbulence in fluid dynamics. History The concept of HRT was introduced to the medical community by Georg Schmidt and colleagues from the Technical University of Munich in 1999 in the British medica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scaling Symmetries
Scaling may refer to: Science and technology Mathematics and physics * Scaling (geometry), a linear transformation that enlarges or diminishes objects * Scale invariance, a feature of objects or laws that do not change if scales of length, energy, or other variables are multiplied by a common factor ** Scaling law, a law that describes the scale invariance found in many natural phenomena * The scaling of critical exponents in physics, such as Widom scaling, or scaling of the renormalization group Computing and information technology * Feature scaling, a method used to standardize the range of independent variables or features of data * Image scaling, the resizing of an image * Multidimensional scaling, a means of visualizing the level of similarity of individual cases of a dataset * Scalability, a computer's or network's ability to function as the number of users increases * Scaling along the Z axis, a technique used in computer graphics for a pseudo-3D effect * Reduced scales ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heart Rate Variability
Heart rate variability (HRV) is the physiological phenomenon of variation in the time interval between heartbeats. It is measured by the variation in the beat-to-beat interval. Other terms used include: "cycle length variability", "R–R variability" (where R is a point corresponding to the peak of the QRS complex of the ECG wave; and RR is the interval between successive Rs), and "heart period variability". Methods used to detect beats include: ECG, blood pressure, ballistocardiograms, and the pulse wave signal derived from a photoplethysmograph (PPG). ECG is considered the gold standard for HRV measurement because it provides a direct reflection of cardiac electric activity. Clinical significance Reduced HRV has been shown to be a predictor of mortality after myocardial infarction although others have shown that the information in HRV relevant to acute myocardial infarction survival is fully contained in the mean heart rate. A range of other outcomes and conditions may al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré section, transversal to the flow of the system. More precisely, one considers a periodic orbit with initial conditions within a section of the space, which leaves that section afterwards, and observes the point at which this orbit first returns to the section. One then creates a map to send the first point to the second, hence the name ''first recurrence map''. The transversality of the Poincaré section means that periodic orbits starting on the subspace flow through it and not parallel to it. A Poincaré map can be interpreted as a discrete dynamical system with a state space that is one dimension smaller than the original continuous dynamical system. Because it preserves many properties of periodic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Plot
In descriptive statistics and chaos theory, a recurrence plot (RP) is a plot showing, for each moment i in time, the times at which the state of a dynamical system returns to the previous state at i, i.e., when the phase space trajectory visits roughly the same area in the phase space as at time j. In other words, it is a plot of :\vec(i)\approx \vec(j), showing i on a horizontal axis and j on a vertical axis, where \vec is the state of the system (or its phase space trajectory). Background Natural processes can have a distinct recurrent behaviour, e.g. periodicities (as seasonal or Milankovich cycles), but also irregular cyclicities (as El Niño Southern Oscillation, heart beat intervals). Moreover, the recurrence of states, in the meaning that states are again arbitrarily close after some time of divergence, is a fundamental property of deterministic dynamical systems and is typical for nonlinear or chaotic systems (cf. Poincaré recurrence theorem). The recurrence of states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autonomic Nervous System
The autonomic nervous system (ANS), formerly referred to as the vegetative nervous system, is a division of the peripheral nervous system that supplies internal organs, smooth muscle and glands. The autonomic nervous system is a control system that acts largely unconsciously and regulates bodily functions, such as the heart rate, its force of contraction, digestion, respiratory rate, pupillary response, urination, and sexual arousal. This system is the primary mechanism in control of the fight-or-flight response. The autonomic nervous system is regulated by integrated reflexes through the brainstem to the spinal cord and organs. Autonomic functions include control of respiration, cardiac regulation (the cardiac control center), vasomotor activity (the vasomotor center), and certain reflex actions such as coughing, sneezing, swallowing and vomiting. Those are then subdivided into other areas and are also linked to autonomic subsystems and the peripheral nervous syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heart Rate
Heart rate (or pulse rate) is the frequency of the heartbeat measured by the number of contractions (beats) of the heart per minute (bpm). The heart rate can vary according to the body's physical needs, including the need to absorb oxygen and excrete carbon dioxide, but is also modulated by numerous factors, including, but not limited to, genetics, physical fitness, stress or psychological status, diet, drugs, hormonal status, environment, and disease/illness as well as the interaction between and among these factors. It is usually equal or close to the pulse measured at any peripheral point. The American Heart Association states the normal resting adult human heart rate is 60–100 bpm. Tachycardia is a high heart rate, defined as above 100 bpm at rest. Bradycardia is a low heart rate, defined as below 60 bpm at rest. When a human sleeps, a heartbeat with rates around 40–50 bpm is common and is considered normal. When the heart is not beating in a regular pattern, this i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repolarization
In neuroscience, repolarization refers to the change in membrane potential that returns it to a negative value just after the depolarization phase of an action potential which has changed the membrane potential to a positive value. The repolarization phase usually returns the membrane potential back to the resting membrane potential. The efflux of potassium (K+) ions results in the falling phase of an action potential. The ions pass through the selectivity filter of the K+ channel pore. Repolarization typically results from the movement of positively charged K+ ions out of the cell. The repolarization phase of an action potential initially results in hyperpolarization, attainment of a membrane potential, termed the afterhyperpolarization, that is more negative than the resting potential. Repolarization usually takes several milliseconds. Repolarization is a stage of an action potential in which the cell experiences a decrease of voltage due to the efflux of potassium (K+) ions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Plot
In descriptive statistics and chaos theory, a recurrence plot (RP) is a plot showing, for each moment i in time, the times at which the state of a dynamical system returns to the previous state at i, i.e., when the phase space trajectory visits roughly the same area in the phase space as at time j. In other words, it is a plot of :\vec(i)\approx \vec(j), showing i on a horizontal axis and j on a vertical axis, where \vec is the state of the system (or its phase space trajectory). Background Natural processes can have a distinct recurrent behaviour, e.g. periodicities (as seasonal or Milankovich cycles), but also irregular cyclicities (as El Niño Southern Oscillation, heart beat intervals). Moreover, the recurrence of states, in the meaning that states are again arbitrarily close after some time of divergence, is a fundamental property of deterministic dynamical systems and is typical for nonlinear or chaotic systems (cf. Poincaré recurrence theorem). The recurrence of states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |