|
Percentage Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
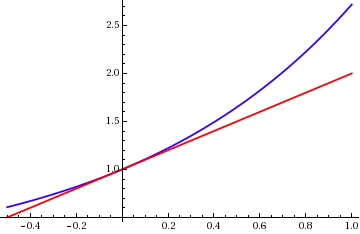
E^x With Linear Approximation
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kelvin Scale
The kelvin, symbol K, is the primary unit of temperature in the International System of Units (SI), used alongside its prefixed forms and the degree Celsius. It is named after the Belfast-born and University of Glasgow-based engineer and physicist William Thomson, 1st Baron Kelvin (1824–1907). The Kelvin scale is an absolute thermodynamic temperature scale, meaning it uses absolute zero as its null (zero) point. Historically, the Kelvin scale was developed by shifting the starting point of the much-older Celsius scale down from the melting point of water to absolute zero, and its increments still closely approximate the historic definition of a degree Celsius, but since 2019 the scale has been defined by fixing the Boltzmann constant to be exactly . Hence, one kelvin is equal to a change in the thermodynamic temperature that results in a change of thermal energy by . The temperature in degree Celsius is now defined as the temperature in kelvins minus 273.15, meaning t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Round-off Error
A roundoff error, also called rounding error, is the difference between the result produced by a given algorithm using exact arithmetic and the result produced by the same algorithm using finite-precision, rounded arithmetic. Rounding errors are due to inexactness in the representation of real numbers and the arithmetic operations done with them. This is a form of quantization error. When using approximation equations or algorithms, especially when using finitely many digits to represent real numbers (which in theory have infinitely many digits), one of the goals of numerical analysis is to estimate computation errors. Computation errors, also called numerical errors, include both truncation errors and roundoff errors. When a sequence of calculations with an input involving any roundoff error are made, errors may accumulate, sometimes dominating the calculation. In ill-conditioned problems, significant error may accumulate. In short, there are two major facets of roundoff e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Difference
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the "sizes" of the things being compared, i.e. dividing by a ''standard'' or ''reference'' or ''starting'' value. The comparison is expressed as a ratio and is a unitless number. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent(age) difference, or relative percentage difference are also commonly used. The terms "change" and "difference" are used interchangeably. Relative change is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change (relative change expressed as a percentage) called ''percent error'' occurs in measuring situations where the reference value is the accepted or actual value (perhaps theoretically determined) and the value being compared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantization Error
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set (often a continuous set) to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms. The difference between an input value and its quantized value (such as round-off error) is referred to as quantization error. A device or algorithmic function that performs quantization is called a quantizer. An analog-to-digital converter is an example of a quantizer. Example For example, rounding a real number x to the nearest integer value forms a very basic type of quantizer – a ''uniform'' one. A typical (''mid-tread'') un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propagation Of Uncertainty
In statistics, propagation of uncertainty (or propagation of error) is the effect of variables' uncertainties (or errors, more specifically random errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g., instrument precision) which propagate due to the combination of variables in the function. The uncertainty ''u'' can be expressed in a number of ways. It may be defined by the absolute error . Uncertainties can also be defined by the relative error , which is usually written as a percentage. Most commonly, the uncertainty on a quantity is quantified in terms of the standard deviation, , which is the positive square root of the variance. The value of a quantity and its error are then expressed as an interval . If the statistical probability distribution of the variable is known or can be assumed, it is possible to derive confidence limits to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement Uncertainty
In metrology, measurement uncertainty is the expression of the statistical dispersion of the values attributed to a measured quantity. All measurements are subject to uncertainty and a measurement result is complete only when it is accompanied by a statement of the associated uncertainty, such as the standard deviation. By international agreement, this uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity value. It is a non-negative parameter. The measurement uncertainty is often taken as the standard deviation of a state-of-knowledge probability distribution over the possible values that could be attributed to a measured quantity. Relative uncertainty is the measurement uncertainty relative to the magnitude of a particular single choice for the value for the measured quantity, when this choice is nonzero. This particular single choice is usually called the measured value, which may be optimal in some well-defined sense (e.g., a mean, median, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement Error
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. In statistics, an error is not necessarily a "mistake". Variability is an inherent part of the results of measurements and of the measurement process. Measurement errors can be divided into two components: ''random'' and ''systematic''. Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system. Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged. Measurement errors can be summarized in terms of accuracy and precision. Measurement error should not be confused with measuremen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Epsilon
Machine epsilon or machine precision is an upper bound on the relative approximation error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science. The quantity is also called macheps and it has the symbols Greek epsilon \varepsilon. There are two prevailing definitions. In numerical analysis, machine epsilon is dependent on the type of rounding used and is also called unit roundoff, which has the symbol bold Roman u. However, by a less formal, but more widely-used definition, machine epsilon is independent of rounding method and may be equivalent to u or 2u. Values for standard hardware arithmetics The following table lists machine epsilon values for standard floating-point formats. Each format uses round-to-nearest. Formal definition ''Rounding'' is a procedure for choosing the representation of a real number in a floating point number syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Experimental Uncertainty Analysis
Experimental uncertainty analysis is a technique that analyses a ''derived'' quantity, based on the uncertainties in the experimentally ''measured'' quantities that are used in some form of mathematical relationship (" model") to calculate that derived quantity. The model used to convert the measurements into the derived quantity is usually based on fundamental principles of a science or engineering discipline. The uncertainty has two components, namely, bias (related to '' accuracy'') and the unavoidable random variation that occurs when making repeated measurements (related to '' precision''). The measured quantities may have biases, and they certainly have random variation, so what needs to be addressed is how these are "propagated" into the uncertainty of the derived quantity. Uncertainty analysis is often called the "propagation of error." Introduction For example, an experimental uncertainty analysis of an undergraduate physics lab experiment in which a pendulum can es ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its " true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condition Number
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. In linear regression the condition number of the moment matrix can be used as a diagnostic for multicollinearity. The condition number is an application of the derivative, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |