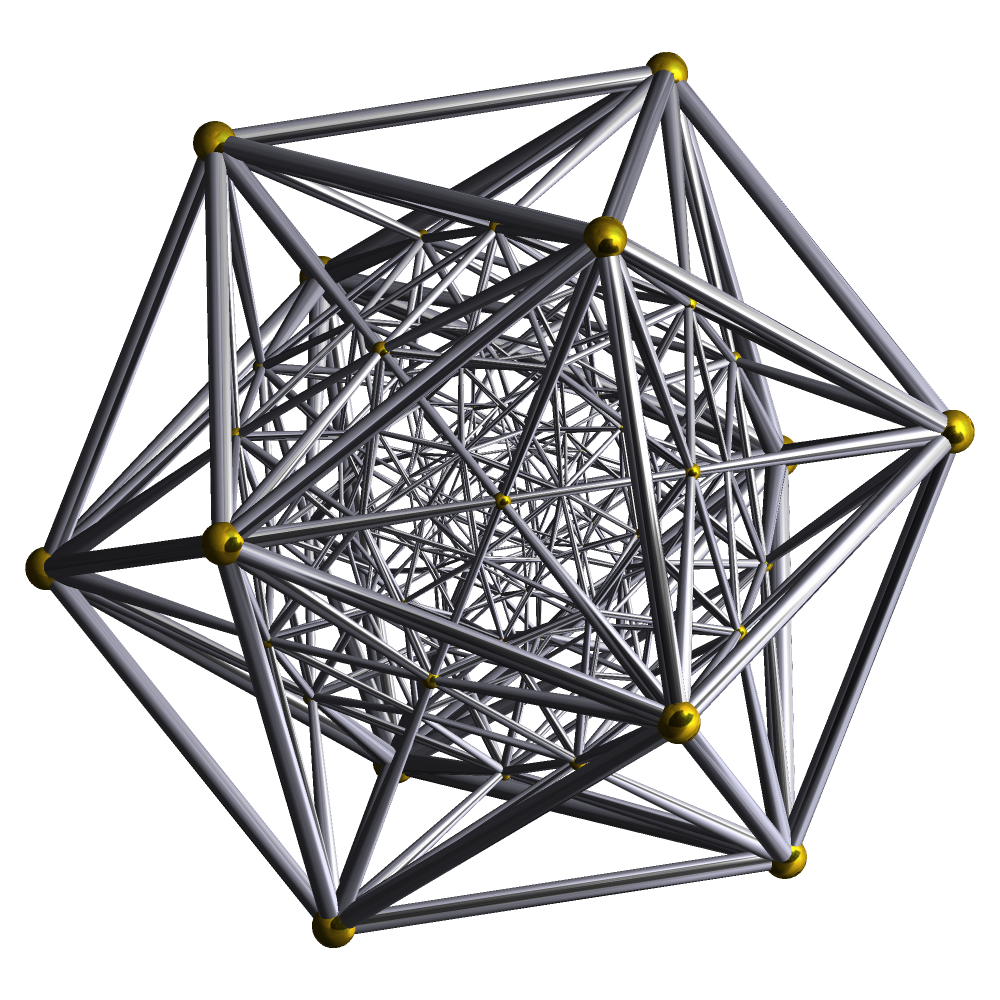
|
Pentagrammic-order 600-cell Honeycomb
In the geometry of hyperbolic 4-space, the pentagrammic-order 600-cell honeycomb is one of four regular star-honeycombs. With Schläfli symbol , it has five 600-cells around each face in a pentagrammic arrangement. It is dual to the small stellated 120-cell honeycomb. It can be considered the higher-dimensional analogue of the 4-dimensional icosahedral 120-cell and the 3-dimensional great dodecahedron. It is related to the order-5 icosahedral 120-cell honeycomb and great 120-cell honeycomb: the icosahedral 120-cells and great 120-cells in each honeycomb are replaced by the 600-cells that are their convex hulls, thus forming the pentagrammic-order 600-cell honeycomb. This honeycomb can also be constructed by taking the order-5 5-cell honeycomb and replacing clusters of 600 5-cells meeting at a vertex with 600-cells. Each 5-cell belongs to five such clusters, and thus the pentagrammic-order 600-cell honeycomb has density 5. See also * List of regular polytopes This arti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Regular Polytopes
This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ''n''-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an ''n''-polytope equivalently describes a tessellation of an (''n'' − 1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example, the cube has Schläfli symbol , and with its octahedral symmetry, [4,3] or , it is represented by Coxeter diagram . The regular polytopes are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to differentiate it from complex hyperbolic spaces, quaternionic hyperbolic spaces and the octononic hyperbolic plane which are the other symmetric spaces of negative curvature. Hyperbolic space serves as the prototype of a Gromov hyperbolic space which is a far-reachin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density (polytope)
In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets. The same calculation can be performed for any convex polyhedron, even one without symmetries, by choosing any point interior to the polyhedron as its center. For these polyhedra, the density will be 1. More generally, for any non-self-intersecting (acoptic) polyhedron, the density can be computed as 1 by a similar calculation that choose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4- simplex (Coxeter's \alpha_4 polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides. The regular 5-cell is bounded by five regular tetrahedra, and is one of the six regular convex 4-polytopes (the four-dimensional analogues of the Platonic solids). A regular 5-cell can be constructed from a regular tetrahedron by adding a fifth vertex one edge length distant from all the vertices of the tetrahedron. This cannot be done in 3-dimensional space. The regular 5-cell is a solution to the problem: ''Make 10 equilateral triangles, all of the same size, using 10 m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order-5 5-cell Honeycomb
In the geometry of hyperbolic 4-space, the order-5 5-cell honeycomb is one of five compact regular space-filling tessellations (or honeycombs). With Schläfli symbol , it has five 5-cells around each face. Its dual is the 120-cell honeycomb, . Related honeycombs It is related to the order-5 tesseractic honeycomb, , and order-5 120-cell honeycomb, . It is topologically similar to the finite 5-orthoplex, , and 5-simplex, . It is analogous to the 600-cell, , and icosahedron, . See also * List of regular polytopes References *Coxeter, ''Regular Polytopes'', 3rd. ed., Dover Publications, 1973. . (Tables I and II: Regular polytopes and honeycombs, pp. 294–296) *Coxeter Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to ..., ''The Beauty of Geometry: Twelve Essays'', Dover ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great 120-cell
In geometry, the great 120-cell or great polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is one of the two such polytopes that is self-dual. Related polytopes It has the same edge arrangement as the 600-cell, icosahedral 120-cell as well as the same face arrangement as the grand 120-cell. Due to its self-duality, it does not have a good three-dimensional analogue, but (like all other star polyhedra and polychora) is analogous to the two-dimensional pentagram. See also * List of regular polytopes * Convex regular 4-polytope * Kepler-Poinsot solids regular star polyhedron * Star polygon regular star polygons References * Edmund Hess, (1883) ''Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder' * Coxeter, H. S. M. Coxeter, ''Regular Polytopes'', 3rd. ed., Dover Publications, 1973. . * Jo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great 120-cell Honeycomb
In the geometry of hyperbolic 4-space, the great 120-cell honeycomb is one of four regular star- honeycombs. With Schläfli symbol , it has three great 120-cells around each face. It is dual to the order-5 icosahedral 120-cell honeycomb. It can be seen as a greatening of the 120-cell honeycomb, and is thus analogous to the three-dimensional great dodecahedron and four-dimensional great 120-cell . It has density 10. See also * List of regular polytopes This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ' ... References * Coxeter, '' Regular Polytopes'', 3rd. ed., Dover Publications, 1973. . (Tables I and II: Regular polytopes and honeycombs, pp. 294–296) * Coxeter, ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999 (Chapter 10: Regular honeycombs in hyper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order-5 Icosahedral 120-cell Honeycomb
In the geometry of hyperbolic 4-space, the order-5 icosahedral 120-cell honeycomb is one of four regular star- honeycombs. With Schläfli symbol , it has five icosahedral 120-cells around each face. It is dual to the great 120-cell honeycomb. It can be constructed by replacing the great dodecahedral cells of the great 120-cell honeycomb with their icosahedral convex hulls, thus replacing the great 120-cells with icosahedral 120-cells. It is thus analogous to the four-dimensional icosahedral 120-cell. It has density 10. See also * List of regular polytopes This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ' ... References * Coxeter, '' Regular Polytopes'', 3rd. ed., Dover Publications, 1973. . (Tables I and II: Regular polytopes and honeycombs, pp. 294–296) * Coxeter, ''Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Dodecahedron
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex. The discovery of the great dodecahedron is sometimes credited to Louis Poinsot in 1810, though there is a drawing of something very similar to a great dodecahedron in the 1568 book '' Perspectiva Corporum Regularium'' by Wenzel Jamnitzer. The great dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the -pentagonal polytope faces of the core -polytope (pentagons for the great dodecahedron, and line segments for the pentagram) until the figure again closes. Images Related polyhedra It shares the same edge arrangement as the convex regular icosahedron; the compound with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedral 120-cell
In geometry, the icosahedral 120-cell, polyicosahedron, faceting, faceted 600-cell or icosaplex is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is constructed by 5 icosahedron, icosahedra around each edge in a pentagrammic figure. The vertex figure is a great dodecahedron. Related polytopes It has the same edge arrangement as the 600-cell, grand 120-cell and great 120-cell, and shares its vertices with all other Schläfli–Hess 4-polytopes except the great grand stellated 120-cell (another stellation of the 120-cell). As a faceted 600-cell, replacing the tetrahedron, simplicial cells of the 600-cell with icosahedron, icosahedral pentagonal polytope cells, it could be seen as a four-dimensional analogue of the great dodecahedron, which replaces the triangular faces of the icosahedron with pentagonal faces. Indeed, the icosahedral 120-cell is dual to the small stellated 120-cell, which could be taken as a 4D analogue of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Stellated 120-cell Honeycomb
In the geometry of hyperbolic 4-space, the small stellated 120-cell honeycomb is one of four regular star-honeycombs. With Schläfli symbol , it has three small stellated 120-cells around each face. It is dual to the pentagrammic-order 600-cell honeycomb. It can be seen as a stellation of the 120-cell honeycomb, and is thus analogous to the three-dimensional small stellated dodecahedron and four-dimensional small stellated 120-cell . It has density 5. See also * List of regular polytopes This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ' ... References * Coxeter, '' Regular Polytopes'', 3rd. ed., Dover Publications, 1973. . (Tables I and II: Regular polytopes and honeycombs, pp. 294–296) * Coxeter, ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polytope
In geometry, every polyhedron is associated with a second dual structure, where the Vertex (geometry), vertices of one correspond to the Face (geometry), faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or Abstract polytope, abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the Symmetry, symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is #Self-dual polyhedra, self-dual. The dual of an Isogonal figure, isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
