|
Pedoe's Inequality
In geometry, Pedoe's inequality (also Neuberg–Pedoe inequality), named after Daniel Pedoe (1910–1998) and Joseph Jean Baptiste Neuberg (1840–1926), states that if ''a'', ''b'', and ''c'' are the lengths of the sides of a triangle with area ''ƒ'', and ''A'', ''B'', and ''C'' are the lengths of the sides of another triangle with area ''F'', then :A^2(b^2+c^2-a^2)+B^2(a^2+c^2-b^2)+C^2(a^2+b^2-c^2)\geq 16Ff,\, with equality if and only if the two triangles are similar with pairs of corresponding sides (''A, a''), (''B, b''), and (''C, c''). The expression on the left is not only symmetric under any of the six permutations of the set of pairs, but also—perhaps not so obviously—remains the same if ''a'' is interchanged with ''A'' and ''b'' with ''B'' and ''c'' with ''C''. In other words, it is a symmetric function of the pair of triangles. Pedoe's inequality is a generalization of Weitzenböck's inequality, which is the case in which one of the triang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Pedoe
Dan Pedoe (29 October 1910, London – 27 October 1998, St Paul, Minnesota, USA) was an English-born mathematician and geometer with a career spanning more than sixty years. In the course of his life he wrote approximately fifty research and expository papers in geometry. He is also the author of various core books on mathematics and geometry some of which have remained in print for decades and been translated into several languages. These books include the three-volume ''Methods of Algebraic Geometry'' (which he wrote in collaboration with W. V. D. Hodge), ''The Gentle Art of Mathematics'', ''Circles: A Mathematical View'', ''Geometry and the Visual Arts'' and most recently ''Japanese Temple Geometry Problems: San Gaku'' (with Hidetoshi Fukagawa). Early life Daniel Pedoe was born in London in 1910, the youngest of thirteen children of Szmul Abramski, a Jewish immigrant from Poland who found himself in London in the 1890s: he had boarded a cattle boat not knowing whether it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Jean Baptiste Neuberg
Joseph Jean Baptiste Neuberg (30 October 1840 – 22 March 1926) was a Luxembourgish mathematician who worked primarily in geometry. Biography Neuberg was born on 30 October 1840 in Luxembourg City, Luxembourg. He first studied at a local school, the Athénée de Luxembourg, then progressed to Ghent University, studying at the École normale des Sciences of the science faculty. After graduation, Neuberg taught at several institutions. Between 1862 and 1865, he taught at the École Normale de Nivelle. For the next sixteen years, he taught at the Athénée Royal d'Arlon, though he also taught at the École Normale at Bruges from 1868 onwards. Retrieved on 2008-09-16. Neuberg switched from his previous two schools to the Athénée Royal de Liège in 1878. He became an extraordinary professor in the university in the same city in 1884, and was promoted to ordinary professor in 1887. He held this latter position until his retirement in 1910. A year after his retirement, he was ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (geometry), scaling (enlarging or reducing), possibly with additional translation (geometry), translation, rotation (mathematics), rotation and reflection (mathematics), reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruence (geometry), congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Corresponding Sides
In geometry, the tests for congruence and similarity involve comparing corresponding sides and corresponding angles of polygons. In these tests, each side and each angle in one polygon is paired with a side or angle in the second polygon, taking care to preserve the order of adjacency. For example, if one polygon has sequential sides , , , , and and the other has sequential sides , , , , and , and if and are corresponding sides, then side (adjacent to ) must correspond to either or (both adjacent to ). If and correspond to each other, then corresponds to , corresponds to , and corresponds to ; hence the th element of the sequence corresponds to the th element of the sequence for On the other hand, if in addition to corresponding to we have corresponding to , then the th element of corresponds to the th element of the reverse sequence . Congruence tests look for all pairs of corresponding sides to be equal in length, though except in the case of the triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set can mean one of two different things: * an arrangement of its members in a sequence or linear order, or * the act or process of changing the linear order of an ordered set. An example of the first meaning is the six permutations (orderings) of the set : written as tuples, they are (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). Anagrams of a word whose letters are all different are also permutations: the letters are already ordered in the original word, and the anagram reorders them. The study of permutations of finite sets is an important topic in combinatorics and group theory. Permutations are used in almost every branch of mathematics and in many other fields of science. In computer science, they are used for analyzing sorting algorithms; in quantum physics, for describing states of particles; and in biology, for describing RNA sequences. The number of permutations of distinct objects is factorial, us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties. The equilateral triangle can be found in various tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry. Properties An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its base. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heron's Formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths Letting be the semiperimeter of the triangle, s = \tfrac12(a + b + c), the area is A = \sqrt. It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work ''Metrica'', though it was probably known centuries earlier. Example Let be the triangle with sides , , and . This triangle's semiperimeter is s = \tfrac12(a+b+c)= \tfrac12(4+13+15) = 16 therefore , , , and the area is \begin A &= \\ mu&= \\ mu&= 24. \end In this example, the triangle's side lengths and area are integers, making it a Heronian triangle. However, Heron's formula works equally well when the side lengths are real numbers. As long as they obey the strict triangle inequality, they define a triangle in the Euclidean plane whose area is a positive real number. Alternate expressions Heron's formula can also be written in terms of just ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
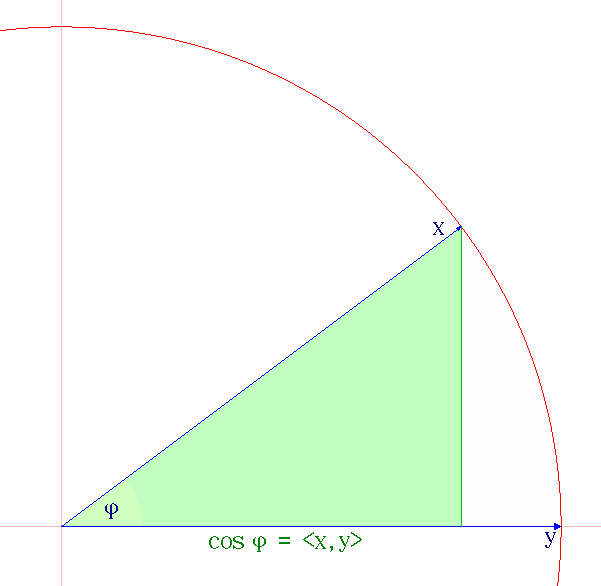
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |