|
Parabolic Equation
A parabolic partial differential equation is a type of partial differential equation (PDE). Parabolic PDEs are used to describe a wide variety of time-dependent phenomena, including heat conduction, particle diffusion, and pricing of derivative investment instruments. Definition To define the simplest kind of parabolic PDE, consider a real-valued function u(x, y) of two independent real variables, x and y. A second-order, linear, constant-coefficient PDE for u takes the form :Au_ + 2Bu_ + Cu_ + Du_x + Eu_y + F = 0, and this PDE is classified as being ''parabolic'' if the coefficients satisfy the condition :B^2 - AC = 0. Usually x represents one-dimensional position and y represents time, and the PDE is solved subject to prescribed initial and boundary conditions. The name "parabolic" is used because the assumption on the coefficients is the same as the condition for the analytic geometry equation A x^2 + 2B xy + C y^2 + D x + E y + F = 0 to define a planar parabola. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Singularity
In mathematics, a singularity is a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as by lacking differentiability or analyticity. For example, the real function : f(x) = \frac has a singularity at x = 0, where the numerical value of the function approaches \pm\infty so the function is not defined. The absolute value function g(x) = , x, also has a singularity at x = 0, since it is not differentiable there. The algebraic curve defined by \left\ in the (x, y) coordinate system has a singularity (called a cusp) at (0, 0). For singularities in algebraic geometry, see singular point of an algebraic variety. For singularities in differential geometry, see singularity theory. Real analysis In real analysis, singularities are either discontinuities, or discontinuities of the derivative (sometimes also discontinuities of higher order derivatives). There are four kinds of discon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe was the first president and Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance, due to concerns about competing with the American Journal of Mathematics. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influential in in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autowave
Autowaves are self-supporting non-linear waves in active media (i.e. those that provide distributed energy sources). The term is generally used in processes where the waves carry relatively low energy, which is necessary for synchronization or switching the active medium. Introduction Relevance and significance In 1980, the Soviet scientists G.R. Ivanitsky, V.I. Krinsky, A.N. Zaikin, A.M. Zhabotinsky, B.P. Belousov became winners of the highest state award of the USSR, Lenin Prize "''for the discovery of a new class of autowave processes and the study of them in disturbance of stability of the distributed excitable systems''." A brief history of autowave researches The first who studied actively the self-oscillations was Academician AA Andronov, and the term "''auto-oscillations''" in Russian terminology was introduced by AA Andronov in 1928. His followers from Lobachevsky University further contributed greatly to the development of ''autowave theory''. The s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Partial Differential Equation
Second-order linear partial differential equations (PDEs) are classified as either elliptic, hyperbolic, or parabolic. Any second-order linear PDE in two variables can be written in the form :Au_ + 2Bu_ + Cu_ + Du_x + Eu_y + Fu +G= 0,\, where , , , , , , and are functions of and and where u_x=\frac, u_=\frac and similarly for u_,u_y,u_. A PDE written in this form is elliptic if :B^2-AC, applying the chain rule once gives :u_=u_\xi \xi_x+u_\eta \eta_x and u_=u_\xi \xi_y+u_\eta \eta_y, a second application gives :u_=u_ _x+u_ _x+2u_\xi_x\eta_x+u_\xi_+u_\eta_, :u_=u_ _y+u_ _y+2u_\xi_y\eta_y+u_\xi_+u_\eta_, and :u_=u_ \xi_x\xi_y+u_ \eta_x\eta_y+u_(\xi_x\eta_y+\xi_y\eta_x)+u_\xi_+u_\eta_. We can replace our PDE in x and y with an equivalent equation in \xi and \eta :au_ + 2bu_ + cu_ \text= 0,\, where :a=A^2+2B\xi_x\xi_y+C^2, :b=2A\xi_x\eta_x+2B(\xi_x\eta_y+\xi_y\eta_x) +2C\xi_y\eta_y , and :c=A^2+2B\eta_x\eta_y+C^2. To transform our PDE into the desired canonical fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Partial Differential Equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first n-1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is : \frac = c^2 \frac The equation has the property that, if ''u'' and its first time derivative are arbitrarily specified initial data on the line (with sufficient smoothness properties), then there exists a solution for all time ''t''. The solutions of hyperbolic equations are "wave-like". If a disturbance is made in the initial data of a hyperbolic differential equation, then not every point of space feels the disturbance at once. Rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Curvature Flow
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold (for example, smooth surfaces in 3-dimensional Euclidean space). Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly (since the mean curvature vector of a sphere points inward). Except in special cases, the mean curvature flow develops singularities. Under the constraint that volume enclosed is constant, this is called surface tension flow. It is a parabolic partial differential equation, and can be interpreted as "smoothing". Existence and uniqueness The following was shown by Michael Gage and Richard S. Hamilton as an application of Hamilton's general existence theorem for parabolic geometric f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-posed
The mathematical term well-posed problem stems from a definition given by 20th-century French mathematician Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that: # a solution exists, # the solution is unique, # the solution's behaviour changes continuously with the initial conditions. Examples of archetypal well-posed problems include the Dirichlet problem for Laplace's equation, and the heat equation with specified initial conditions. These might be regarded as 'natural' problems in that there are physical processes modelled by these problems. Problems that are not well-posed in the sense of Hadamard are termed ill-posed. Inverse problems are often ill-posed. For example, the inverse heat equation, deducing a previous distribution of temperature from final data, is not well-posed in that the solution is highly sensitive to changes in the final data. Continuum models must often be discretized in order to obtain a numerica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ricci Flow
In the mathematical fields of differential geometry and geometric analysis, the Ricci flow ( , ), sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation. The Ricci flow, so named for the presence of the Ricci tensor in its definition, was introduced by Richard Hamilton, who used it through the 1980s to prove striking new results in Riemannian geometry. Later extensions of Hamilton's methods by various authors resulted in new applications to geometry, including the resolution of the differentiable sphere conjecture by Simon Brendle and Richard Schoen. Following Shing-Tung Yau's suggestion that the singularities of solutions of the Ricci flow could identify the topo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solution Of The Poincaré Conjecture
*
{{disambiguation ...
Solution may refer to: * Solution (chemistry), a mixture where one substance is dissolved in another * Solution (equation), in mathematics ** Numerical solution, in numerical analysis, approximate solutions within specified error bounds * Solution, in problem solving * Solution, in solution selling Other uses * V-STOL Solution, an ultralight aircraft * Solution (band), a Dutch rock band ** ''Solution'' (Solution album), 1971 * Solution A.D., an American rock band * ''Solution'' (Cui Jian album), 1991 * ''Solutions'' (album), a 2019 album by K.Flay See also * The Solution (other) The Solution may refer to: * ''The Solution'' (Mannafest album), an album by indie rock band Mannafest * ''The Solution'' (Beanie Sigel album), an album by rapper Beanie Sigel * ''The Solution'' (Buckshot and 9th Wonder album), a collaboration albu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
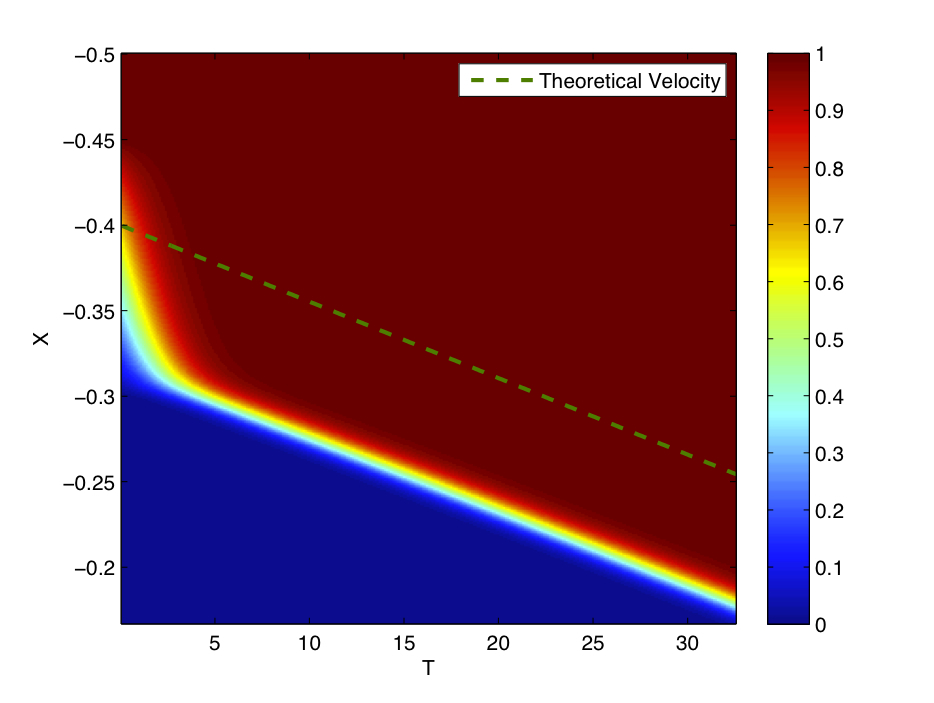
Fisher's Equation
In mathematics, Fisher's equation (named after statistician and biologist Ronald Fisher) also known as the Kolmogorov–Petrovsky–Piskunov equation (named after Andrey Kolmogorov, Ivan Petrovsky, and Nikolai Piskunov), KPP equation or Fisher–KPP equation is the partial differential equation: : \frac - D \frac = r u(1-u).\, It is a kind of reaction–diffusion system that can be used to model population growth and wave propagation. Details Fisher's equation belongs to the class of reaction–diffusion equation: in fact, it is one of the simplest semilinear reaction-diffusion equations, the one which has the inhomogeneous term : f(u,x,t) = r u (1-u),\, which can exhibit traveling wave solutions that switch between equilibrium states given by f(u) = 0. Such equations occur, e.g., in ecology, physiology, combustion, crystallization, plasma physics, and in general phase transition problems. Fisher proposed this equation in his 1937 paper ''The wave of advance of advanta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
