|
Pancyclic Graph
In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph.. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length. Definitions An ''n''-vertex graph ''G'' is pancyclic if, for every k in the range 3 \leq k \leq n \; ,G contains a cycle of length k. It is node-pancyclic or vertex-pancyclic if, for every vertex ''v'' and every ''k'' in the same range, it contains a cycle of length ''k'' that contains ''v''.. Similarly, it is edge-pancyclic if, for every edge ''e'' and every ''k'' in the same range, it contains a cycle of length ''k'' that contains ''e''. A bipartite graph cannot be pancyclic, because it does not contain any odd-length cycles, but it is said to be bipancyclic if it contains cycles of all even lengths from 4 to ''n''. Planar graphs A maximal outerplanar graph is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pancyclic Octahedron
In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph.. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length. Definitions An ''n''-vertex graph ''G'' is pancyclic if, for every k in the range 3 \leq k \leq n \; ,G contains a cycle of length k. It is node-pancyclic or vertex-pancyclic if, for every vertex ''v'' and every ''k'' in the same range, it contains a cycle of length ''k'' that contains ''v''.. Similarly, it is edge-pancyclic if, for every edge ''e'' and every ''k'' in the same range, it contains a cycle of length ''k'' that contains ''e''. A bipartite graph cannot be pancyclic, because it does not contain any odd-length cycles, but it is said to be bipancyclic if it contains cycles of all even lengths from 4 to ''n''. Planar graphs A maximal outerplanar graph is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halin No 8-cycle
{{geodab ...
Halin may refer to: * Halin, Poland * Halin, Somaliland *Hanlin, Burma Hanlin (also known as Halingyi, Halin and Halim) is a village near Shwebo in the Sagaing Division of Myanmar. In the era of the Pyu city-states it was a city of considerable significance, possibly a local capital replacing Sri Ksetra. Today the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs. A bicubic graph is a cubic bipartite graph. Symmetry In 1932, Ronald M. Foster began collecting examples of cubic symmetric graphs, forming the start of the Foster census.. Many well-known individual graphs are cubic and symmetric, including the utility graph, the Petersen graph, the Heawood graph, the Möbius–Kantor graph, the Pappus graph, the Desargues graph, the Nauru graph, the Coxeter graph, the Tutte–Coxeter graph, the Dyck graph, the Foster graph and the Biggs–Smith graph. W. T. Tutte classified the symmetric cubic graphs by the smallest integer number ''s'' such that each two oriented paths of length ''s'' can be mapped to each other by exactly one symmetry of the graph. He showed that ''s'' is at most 5, and provided examples of graphs with each possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # the problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers to nondeterministic Turing machines, a way of mathematically formalizing the idea of a brute-force search algorithm. Polynomial time refers to an amount of time that is considered "quick" for a de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fleischner's Theorem
In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if is a 2-vertex-connected graph, then the square of is Hamiltonian. it is named after Herbert Fleischner, who published its proof in 1974. Definitions and statement An undirected graph ''G'' is Hamiltonian if it contains a cycle that touches each of its vertices exactly once. It is 2-vertex-connected if it does not have an articulation vertex, a vertex whose deletion would leave the remaining graph disconnected. Not every 2-vertex-connected graph is Hamiltonian; counterexamples include the Petersen graph and the complete bipartite graph ''K''2,3. The square of ''G'' is a graph ''G''2 that has the same vertex set as ''G'', and in which two vertices are adjacent if and only if they have distance at most two in ''G''. Fleischner's theorem states that the square of a finite 2-vertex-connected graph with at least three vertices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-vertex-connected Graph
In graph theory, a connected graph is said to be -vertex-connected (or -connected) if it has more than vertices and remains connected whenever fewer than vertices are removed. The vertex-connectivity, or just connectivity, of a graph is the largest for which the graph is -vertex-connected. Definitions A graph (other than a complete graph) has connectivity ''k'' if ''k'' is the size of the smallest subset of vertices such that the graph becomes disconnected if you delete them. Complete graphs are not included in this version of the definition since they cannot be disconnected by deleting vertices. The complete graph with ''n'' vertices has connectivity ''n'' − 1, as implied by the first definition. An equivalent definition is that a graph with at least two vertices is ''k''-connected if, for every pair of its vertices, it is possible to find ''k'' vertex-independent paths connecting these vertices; see Menger's theorem . This definition produces the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Of Graph
In graph theory, a branch of mathematics, the th power of an undirected graph is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in is at most . Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: is called the ''square'' of , is called the ''cube'' of , etc. Graph powers should be distinguished from the products of a graph with itself, which (unlike powers) generally have many more vertices than the original graph. Properties If a graph has diameter , then its -th power is the complete graph. If a graph family has bounded clique-width, then so do its -th powers for any fixed . Coloring Graph coloring on the square of a graph may be used to assign frequencies to the participants of wireless communication networks so that no two participants interfere with each other at any of their common neighbors, and to find graph drawings with high angular resolution. Both the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Bipartite Graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set..Electronic edition page 17. Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete bipartite graphs were already printed as early as 1669, in connection with an edition of the works of Ramon Llull edited by Athanasius Kircher. Llull himself had made similar drawings of complete graphs three centuries earlier.. Definition A complete bipartite graph is a graph whose vertices can be partitioned into two subsets and such that no edge has both endpoints in the same subset, and every possible edge that could connect vertices in different subsets is part of the graph. That is, it is a bipartite graph such that for every two vertices and, is an edge in . A complete bipartite graph w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree is called a graph or regular graph of degree . Also, from the handshaking lemma, a regular graph contains an even number of vertices with odd degree. Regular graphs of degree at most 2 are easy to classify: a graph consists of disconnected vertices, a graph consists of disconnected edges, and a graph consists of a disjoint union of cycles and infinite chains. A graph is known as a cubic graph. A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number of neighbors in common, and every non-adjacent pair of vertices has the same number of neighbors in common. The smallest graphs that are regular but not strong ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strongly Connected Graph
In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(''V'' + ''E'')). Definitions A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first. In a directed graph ''G'' that may not itself be strongly connected, a pair of vertices ''u'' and ''v'' are said to be strongly connected to each other if there is a path in each direction between them. The binary relation of being strongly connected is an equivalence relation, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
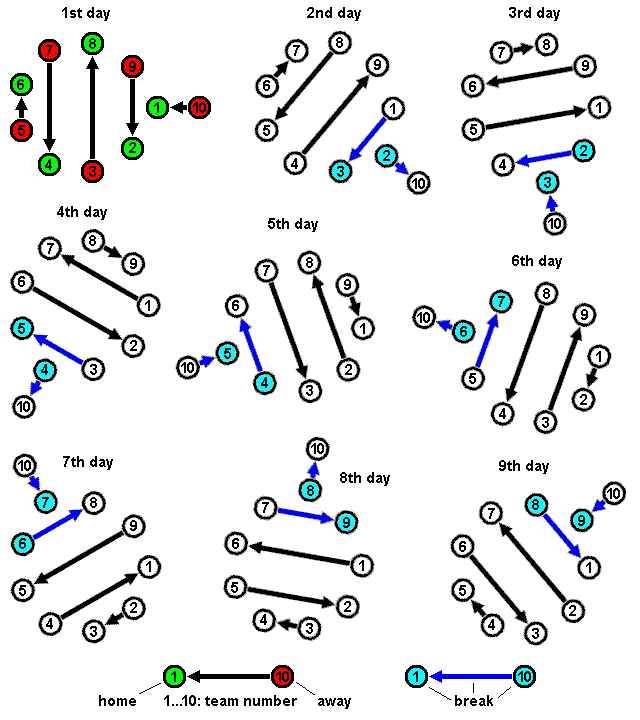
Round-robin Tournament
A round-robin tournament (or all-go-away-tournament) is a competition Competition is a rivalry where two or more parties strive for a common goal which cannot be shared: where one's gain is the other's loss (an example of which is a zero-sum game). Competition can arise between entities such as organisms, indiv ... in which each contestant meets every other participant, usually in turn.''Webster's Third New International Dictionary of the English Language, Unabridged'' (1971, G. & C. Merriam Co), p.1980. A round-robin contrasts with an elimination tournament, in which participants/teams are eliminated after a certain number of losses. Terminology The term ''round-robin'' is derived from the French term ''ruban'', meaning "ribbon". Over a long period of time, the term was Folk etymology, corrupted and idiomized to ''robin''. In a ''single round-robin'' schedule, each participant plays every other participant once. If each participant plays all others twice, this is freque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
