|
Ordered Exponential
The ordered exponential, also called the path-ordered exponential, is a mathematical operation defined in non-commutative algebras, equivalent to the exponential of the integral in the commutative algebras. In practice the ordered exponential is used in matrix and operator algebras. Definition Let be an algebra over a real or complex field , and be a parameterized element of , a : K \to A. The parameter in is often referred to as the ''time parameter'' in this context. The ordered exponential of is denoted \begin \operatorname t) \equiv \mathcal \left\ & \equiv \sum_^\infty \frac \int_0^t \cdots \int_0^t \mathcal \left\ \, dt'_1 \cdots dt'_n \\ & \equiv \sum_^\infty \int_0^t \int_0^ \int_0^ \cdots \int_0^ a(t'_n) \cdots a(t'_1) \, dt'_1 \cdots dt'_ \, dt'_ \, dt'_n \end where the term is equal to 1 and where \mathcal is a higher-order operation that ensures the exponential is time-ordered: any product of that occurs in the expansion of the exponential must be ordere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. In formulas, a limit of a function is usually written as : \lim_ f(x) = L, (although a few authors may use "Lt" instead of "lim") and is read as "the limit of of as approaches equals ". The fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or \rightarrow), as in :f(x) \to L \text x \to c, which reads "f of x tends to L as x tends to c". History Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work ''Opus Geometricum'' (1647): "The ''terminus'' of a pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras over a field. The term ''abstract algebra'' was coined in the early 20th century to distinguish this area of study from older parts of algebra, and more specifically from elementary algebra, the use of variables to represent numbers in computation and reasoning. Algebraic structures, with their associated homomorphisms, form mathematical categories. Category theory is a formalism that allows a unified way for expressing properties and constructions that are similar for various structures. Universal algebra is a related subject that studies types of algebraic structures as single objects. For example, the structure of groups is a single object in universal algebra, which is called the ''variety of groups''. History Before the nineteenth century, algebra meant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
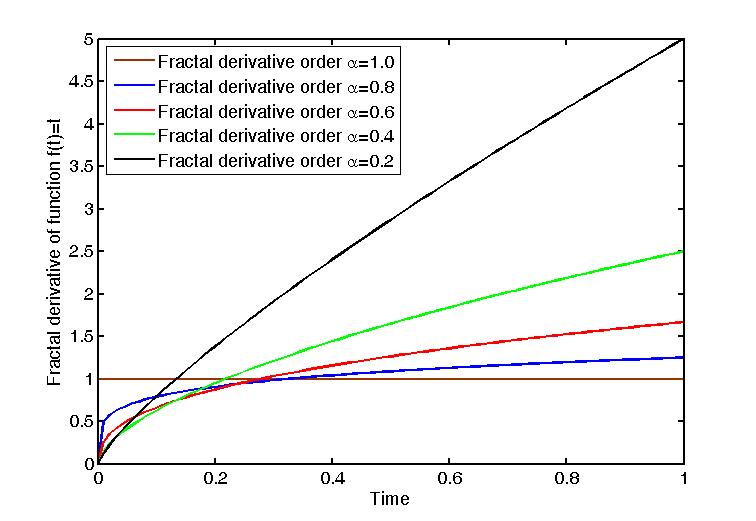
Fractal Derivative
In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the derivative dealing with the measurement of fractals, defined in fractal geometry. Fractal derivatives were created for the study of anomalous diffusion, by which traditional approaches fail to factor in the fractal nature of the media. A fractal measure ''t'' is scaled according to ''tα''. Such a derivative is local, in contrast to the similarly applied fractional derivative. Fractal calculus is formulated as a generalized of standard calculus Physical background Porous media, aquifers, turbulence, and other media usually exhibit fractal properties. Classical diffusion or dispersion laws based on random walks in free space (essentially the same result variously known as Fick's laws of diffusion, Darcy's law, and Fourier's law) are not applicable to fractal media. To address this, concepts such as distance and velocity must be redefined for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Product
In mathematics, the indefinite product operator is the inverse operator of Q(f(x)) = \frac. It is a discrete version of the geometric integral of geometric calculus, one of the non-Newtonian calculi. Some authors use term discrete multiplicative integration. Thus :Q\left( \prod_x f(x) \right) = f(x) \, . More explicitly, if \prod_x f(x) = F(x) , then :\frac = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''CF''(''x'') for any constant ''C''. Therefore, each indefinite product actually represents a family of functions, differing by a multiplicative constant. Period rule If T is a period of function f(x) then :\prod _x f(Tx)=C f(Tx)^ Connection to indefinite sum Indefinite product can be expressed in terms of indefinite sum: :\prod _x f(x)= \exp \left(\sum _x \ln f(x)\right) Alternative usage Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Derivatives And Integrals In Alternative Calculi
There are many alternatives to the classical calculus of Newton and Leibniz; for example, each of the infinitely many non-Newtonian calculi. Occasionally an alternative calculus is more suited than the classical calculus for expressing a given scientific or mathematical idea. The table below is intended to assist people working with the alternative calculus called the "geometric calculus" (or its discrete analog). Interested readers are encouraged to improve the table by inserting citations for verification, and by inserting more functions and more calculi. Table In the following table \psi(x)=\frac is the digamma function, K(x)=e^=e^ is the K-function, (!x)=\frac is subfactorial, B_a(x)=-a\zeta(-a+1,x) are the generalized to real numbers Bernoulli polynomials. See also *Indefinite product *Product integral *Fractal derivative In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the deriva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnus Expansion
In mathematics and physics, the Magnus expansion, named after Wilhelm Magnus (1907–1990), provides an exponential representation of the solution of a first-order homogeneous linear differential equation for a linear operator. In particular, it furnishes the fundamental matrix of a system of linear ordinary differential equations of order with varying coefficients. The exponent is aggregated as an infinite series, whose terms involve multiple integrals and nested commutators. The deterministic case Magnus approach and its interpretation Given the coefficient matrix , one wishes to solve the initial-value problem associated with the linear ordinary differential equation : Y'(t) = A(t) Y(t), \quad Y(t_0) = Y_0 for the unknown -dimensional vector function . When ''n'' = 1, the solution simply reads : Y(t) = \exp \left( \int_^t A(s)\,ds \right) Y_0. This is still valid for ''n'' > 1 if the matrix satisfies for any pair of values of ''t'', ''t''1 an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antisymmetry
In linguistics, antisymmetry is a syntactic theory presented in Richard S. Kayne's 1994 monograph ''The Antisymmetry of Syntax''. It asserts that grammatical hierarchies in natural language follow a universal order, namely specifier-head-complement branching order. The theory is built on the foundation of X-bar theory. Kayne hypothesizes that all phrases whose surface order is not specifier-head-complement have undergone syntactic movements that disrupt this underlying order. Others have posited specifier-complement-head as the basic word order. Antisymmetry as a principle of word order is reliant on X-bar notions such as specifier and complement, the existence of order-altering mechanisms such as movement, and disputed by constituency structure theories (as opposed to dependency structure theories). Asymmetric c-command C-command is a relation between tree nodes, as defined by Tanya Reinhart. Kayne uses a simple definition of c-command based on the "first node up". Howe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exterior Differentiation
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The resulting calculus, known as exterior calculus, allows for a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential -form is thought of as measuring the flux through an infinitesimal - parallelotope at each point of the manifold, then its exterior derivative can be thought of as measuring the net flux through the boundary of a -parallelotope at each point. Definition The exterior derivative of a differential form of degree (also differential -form, or just -form for brevity here) is a differential form of degree . If is a smooth function (a -form), then the exterior derivative of is the differential of . That is, is the unique -form such that for ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Equation
In mathematics, integral equations are equations in which an unknown Function (mathematics), function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,...,x_n ; u(x_1,x_2,x_3,...,x_n) ; I^1 (u), I^2(u), I^3(u), ..., I^m(u)) = 0where I^i(u) is an integral operator acting on ''u.'' Hence, integral equations may be viewed as the analog to differential equations where instead of the equation involving derivatives, the equation contains integrals. A direct comparison can be seen with the mathematical form of the general integral equation above with the general form of a differential equation which may be expressed as follows:f(x_1,x_2,x_3,...,x_n ; u(x_1,x_2,x_3,...,x_n) ; D^1 (u), D^2(u), D^3(u), ..., D^m(u)) = 0where D^i(u) may be viewed as a differential operator of order ''i''. Due to this close connection between differential and integral equations, one can often convert between the two. For examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |